3.7. Плоские антенные решетки

Для получения остронаправленного излучения с узкой пространственной ДН используются плоские антенные решетки (ПАР). Раскрыв ПАР может иметь произвольную форму, но на практике наиболее часто применяются ПАР с прямоугольным, гексагональным и круглым раскрывами. Излучающие элементы ПАР обычно располагают в узлах прямоугольной или треугольной (гексагональной) сетки (рис. 3.8, а) [2].

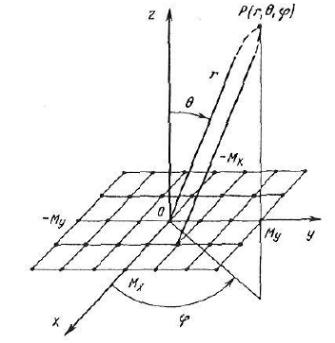
а б

Рис 3.8. Размещение элементов в ПАР

Для анализа направленных свойств ПАР (рис. 3.8, б) воспользуемся общим выражением для множителя системы [2, 5]

.

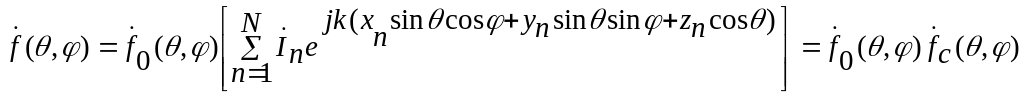Рассмотрим ПАР с прямоугольным раскрывом из изотропных излучателей, расположенных в узлах прямоугольной сетки с центром в начале координат (рис. 3.8, б) Примем, что ПАР состоит из рядов излучателей, параллельных оси y, с расстоянием между рядами . Каждый ряд составлен из излучателей с шагом . Определим координаты излучателей в плоскости раскрыва как ( ) и ( ). Тогда множитель системы преобразуется к виду [2]

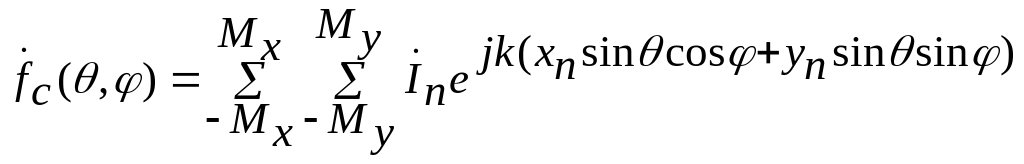. (3.39)

Для анализа направленных свойств ПАР удобно выбрать реализуемое на практике разделяющееся АФР тока в виде произведения двух функций, зависящих только от x и только от y [2]:

. (3.40)

При равноамплитудном возбуждении и линейных законах изменения фаз токов в элементах решетки по координатам x и y

, (3.41)

. (3.42)

При этих условиях для произвольной плоскости (φ=const), проходящей через нормаль к плоскости раскрыва ПАР множитель системы запишется в виде

. (3.43)

Легко убедиться, что каждый из сомножителей в (3.41) есть не что иное, как множитель системы линейной АР, вытянутой вдоль осей x и y с АФР вида (3.41) и (3.42). Сказанное справедливо для любых распределений возбуждающего элементы ПАР тока, характеризуемого функциями, разделяющимися по координатам x и y.

В случае синфазной ПАР фазовые сдвиги токов в соседних по осям x и y элементах и, как следует из (3.43), максимальное излучение ПАР происходит по нормали к плоскости ее раскрыва (рис. 3.9) [15].

В случае линейного фазового распределения при и направление максимального излучения (максимума ГД ДН) рассчитывается из условий обращения в ноль числителей сомножителей в (3.41):

, , (3.44)

в результате чего получаются важные соотношения, позволяющие по заданным углам ориентации ДН ПАР рассчитать требуемые фазовые сдвиги токов в излучателях или решить обратную задачу [2]:

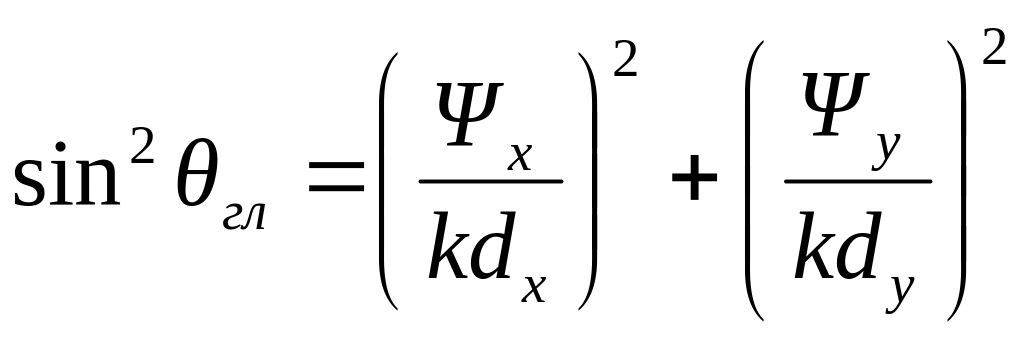, . (3.45)

Выражения (3.43), справедливые для любого амплитудного распределения, используются в теории ФАР и являются основными при решении задачи формирования требуемого для сканирования ДН фазового распределения токов в ее элементах.

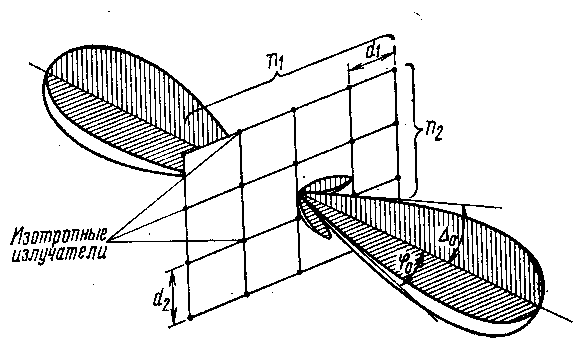
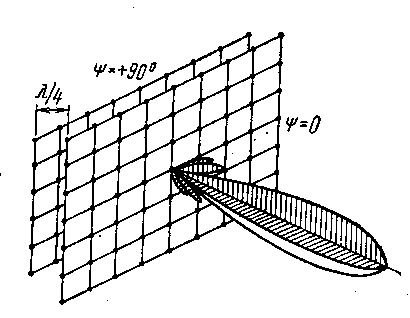
а б

Рис. 3.9. ДН ПАР из изотропных излучателей: без рефлектора (а);

с рефлектором (б)

Для обеспечения отсутствия дополнительных ГЛ в ДН при ее отклонении от нормали к плоскости раскрыва в процессе сканирования значения шага размещения элементов ПАР с прямоугольной сеткой должны удовлетворять условиям [2—5]

, , (3.46)

для ПАР с гексагональной сеткой размещения элементов — менее жесткому условию [2—5]

. (3.47)

КНД синфазной ПАР с прямоугольным раскрывом, составленным из однонаправленных излучателей определяется выражением [2]

, (3.48)

где — КНД эквивалентных линейных АР, параллельных осям x и y. Если размеры раскрыва обозначить как , то для решеток с в итоге получается следующее выражение [2]:

, (3.49)

где — результирующий КИП, — площадь раскрыва, занимаемая элементами ПАР.

В режиме сканирования ДН или при ее фиксированном отклонении от нормали на угол ГЛ ДН расширяется, что приводит к снижению КНД [2—5]:

, (3.50)

Возникновение квадратичных или кубических фазовых искажений распределения токов в ПАР, как и в линейной решетке, также ведет к снижению КНД.