Учебное пособие 1310

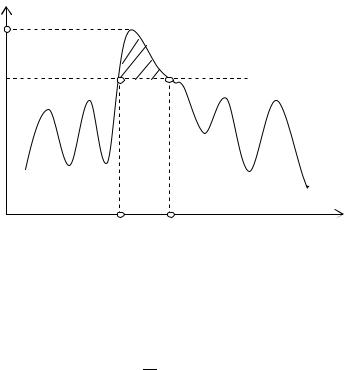
где α (ω,Uд) – некоторый коэффициент, определяемый производительностью рассматриваемой системы.

x(t)

Xп

Зона

Xд

t

t1 t2

Рис. 2.4. Пояснение инцидента

Выражая в нормированном виде функцию ущерба, получаем выражение риска

( ) = ( − 1)(Δ ) ( ),

д

где β – коэффициент, зависящий от α и Xд.

Если осуществить нормирование ( ̅= / д), то последнее выражение примет следующий вид

( ̅=) ( ̅− 1)(Δ ) ( ̅).

Для поиска экстремума риска возьмем производную от риска и приравняем ее нулю. В результате получим

51

̅( ̅)+ ( ̅)− ( ̅) = 0

или

( ̅) = ( ̅)(1− ̅).

К примеру, при нормальном законе распределения

2 ̅− 2(1+ ) ̅− +2 = 0.

В каноническом виде уравнение имеет вид

52

Решение уравнения таково:

̅, = ± ( ) +( ),

т.е. экстремум существует при x0>Xд.

По аналогии подобные решения могут быть получены и для других видов распределения случайной величины x.

Применительно к ИТИ КВО функция ущерба зачастую имеет нелинейный характер. С учетом статданных можно предложить следующую ее конструкцию

( ) = [ −1],

д

где - коэффициент вышеупомянутой нелинейности, задающий крутизну роста ущерба, которая в математическом смысле может привести к неконтролируемому скачку риска и отсутствию у него экстремума, т.е. невозможности нахождения действительного решения следующего уравнения

( ̅) [ ( )+ ̅( )]− ( ) = 0.

В этой связи, научный и практический интерес для КВО представляет управление параметром .

С учетом вышеизложенного перейдем к аналитическому риск-анализу на основе ранее избранного распределения Гумбеля [87].

53

2.2.Параметры и характеристики риска для одной переменной состояния

Рассмотрим ранее избранное распределение Гумбеля, где с учетом результатов раздела 2.1 риск имеет вид

( ) = ( ) ( ) = − 1 . (2.3)

доп

Первоначально определим координатыточки максимума риска (2.3) из следующего уравнения

Упрощая данное выражение, получаем:

54

Осуществим далее диапазонный риск-анализ.

Для нахождения значений ущерба по заданному уровню риска следует решить следующее уравнение:

где k – коэффициент (k<1) задающий уровень отсчета от

– максимума риска. С учетом (2.3) имеем

Разложив логарифм ( − доп) в ряд Тейлора и, ограничившись пятью первыми членами ряда, можно получить уравнений четвертой степени, решаемое в радикалах.

58

2.3. Оценка риска для множества переменных состояния

Когда оценка рисков для отдельных переменных состояний осуществлена, т.е. известны законы распределения риска и найдены его параметры для каждой переменной состояния, представляется возможность рассчитать риск атакуемого объекта в целом. При этом будем исходить из того, что ущербы, возникающие в этих переменных состояний слабо коррелированы между собой. Тогда ожидаемый общий ущерб атакуемого канала можно найти как сумму ущербов в отдельных ее переменных состояний. Причем это допустимо не только для детерминированных, но и для случайных величин. С другой стороны, относительная независимость этих переменных состояний открывает перспективу соответствующих интегральных вероятностных оценок, где вероятность наступления общего ущерба оценивается, как произведение вероятностей возникновения ущербов атакуемого объекта. В этой связи может быть предложено следующее выражение для оценки риска:

где: xi – значение i-ой переменной состояния атакуемого объекта;

59

fi (xi ) – плотность вероятности выпадения экстремальных значений xi ;

n – количество переменных состояния.

При оценке рисков возможно использование пиковых и средних оценок риска.

При пиковой оценке используются координаты максимума риска( ; ), и общее выражение будет выглядеть следующим образом

где: – значение максимума риска в i-ой переменной состояния;

x0*i – значение переменной, при котором имеет место

быть пик риска в i–ой компоненте системы, т.е. мода риска.

При подстановке имеем

Для усредненных оценок общий риск системы можно рассчитать с помощью выражения

60