Методическое пособие 609

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВО «Воронежский государственный технический университет»

И.М. Пашуева А.Н. Шелковой

ЛИНЕЙНАЯ АЛГЕБРА В ЭКОНОМИКЕ

Утверждено учебно-методическим советом университета в качестве учебного пособия

Воронеж 2017

УДК 512.64 ББК 22.143

П 225

Пашуева И.М. Линейная алгебра в экономике: учеб. пособие [Электронный ресурс]. – Электрон. текстовые, граф. данные (1,22 Мб) / И.М. Пашуева, А.Н Шелковой. – Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2017. – 1 электрон. опт. диск (CD-ROM): цв. – Систем. требования: ПК 500 и выше; 256 Мб ОЗУ; Windows XP; SVGA с разрешением 1024x768; Adobe Acrobat; CDROM; мышь. – Загл. с экрана.

Настоящее учебное пособие состоит из шести глав: первая глава посвящена основным понятиям теории множеств, комплексных чисел и алгебры многочленов, во второй и третьей главах рассматриваются методы линейной алгебры, в четвертой главе – векторной алгебры, а в пятой и шестой главах рассматривается применение этих методов к решению экономических задач.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего образования по направлению 38.03.01 «Экономика», профилю «Экономика предприятий и организаций (машиностроение)», дисциплине «Линейная алгебра».

Табл. 2. Ил. 21. Библиогр.: 21 назв.

Рецензенты: кафедра нелинейных колебаний Воронежского государственного университета, д-р физ.-мат. наук, проф. А.Г. Баскаков; канд. физ.-мат. наук, доц. С.П. Майорова

Пашуева И.М., Шелковой А.Н., 2017

ФГБОУ ВО «Воронежский государственный технический университет»,

2017

2

ВВЕДЕНИЕ

Это учебное пособие написано на основе лекций, читаемых одним из авторов на инженерно-экономическом факультете ВГТУ по курсу «Линейная алгебра».

В пособии изложены необходимые основы математического аппарата и примеры его использования в современных экономических приложениях: элементы теории множеств, линейной и векторной алгебры, численных методов линейной алгебры, линейного программирования. Такой объём знаний актуален сегодня для студентов, получающих образование по экономическим специальностям, и соответствует требованиям государственных стандартов по экономическим специальностям.

Изложение материала проведено почти без доказательств – основной упор сделан на приобретение навыков использования математического аппарата. Каждый раздел сопровождается решением характерных задач и соответствующих экономических приложений. Приложения, представляющие в экономике самостоятельный интерес, выделены в отдельный раздел. Пособие содержит также подборку вопросов для повторения, задач и упражнений для самостоятельного решения по каждой теме.

3

ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МНОЖЕСТВ, КОМПЛЕКСНЫХ ЧИСЕЛ И АЛГЕБРЫ МНОГОЧЛЕНОВ

1. Элементы теории множеств и комплексных чисел

1.1. Понятие множества. Операции над множествами

Основателем современной теории множеств считается Георг Кантор. Множество является одним из основных, неопределяемых понятий математики. Оно может содержать конечное или бесконечное число объектов любой природы, однородных по некоторому признаку. Объекты множества называются его элементами. Если множество содержит конечное число элементов, то оно называется конечным множеством, иначе множество называется бесконечным.

Если x – элемент множества X, то пишут: x X (x принадлежит X). Если x не является элементом множества X, то пишут: (читают: x не принадлежит X). Запись означает, что множество X состоит из эле-

ментов x1, x2 , , xn .

Примеры множеств: множество студентов вуза, множество молекул в данном веществе и т.д.

Если множество не содержит ни одного элемента, то оно называется пустым множеством и обозначается .

Пусть X и Y – два множества. Если каждый элемент множества X является элементом множества Y, то множество X называется подмножеством множества Y и пишут: X Y (X содержится в Y) или Y X (Y содержит X).

Свойства подмножеств.

Для любого множества А:

1)A A ;

2)A .

4

Множества A и B называются равными, если они состоят из одних и тех же элементов. Обозначение: A=B . Ясно, что если A Bи B A , то A=B .

Всякое подмножество A данного множества B, которое не совпадает с B и , называется собственным подмноже-

ством B:

Операции над множествами.

Пусть даны два произвольных множества A и B.

Объединением множеств A и B называется множество

C, состоящее из элементов множеств A и B. При этом пишут: A B. Легко видеть, что A A A .

Пересечением множеств A и B называется множество

C, состоящее из элементов, одновременно принадлежащих множеству A и множеству B. Обозначение: A B.

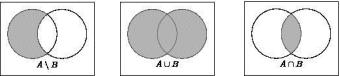
Разностью множеств A и B называется множество R=A\B, состоящее из элементов A, которых нет в B.

Геометрически операции над множествами изобража-

ются с помощью диаграмм Эйлера-Венна (см. рис.1).

Рис.1

Множество, рассматриваемое вместе с каким-нибудь установленным в нём порядком следования элементов, назы-

вается упорядоченным множеством и обозначается:

x1, x2 , , xn .

5

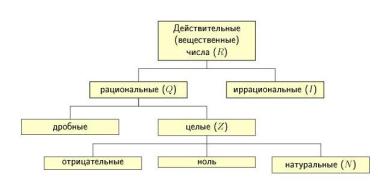
1.2. Числовые множества и их свойства Построение множества действительных чисел.

Рис. 2

Структура множества действительных чисел представлена на рис. 2.

Заметим, что для написания действительных чисел мы используем цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), которые придумали монахи-брамины в Индии; арабы же принесли их в Европу между X и XV столетиями.

Действительные числа образуют множество R элементов, обладающее следующими свойствами:

1.Упорядоченность. Для любых двух действительных чисел a и b определено отношение порядка, т.е. имеет место одно из отношений: a<b, a=b, a>b. При этом, если a<b и b<c,

то a<c (транзитивность упорядоченности). Соотношения порядка называют также сравнением действительных чисел по величине.

2.Операция сложения. Для любой пары чисел a, b R

определено такое единственное число, называемое их суммой a+b, что выполняются условия:

II1. a+b=b+a (коммутативность);

II2. a+(b+c)=(a+b)+c, a, b, c R (ассоциативность);

6

II3. существует единственное число, называемое нулём 0, такое, что a+0=a для любого a R ;

II4. для любого числа a R существует единственное число (-a), называемое ему противоположным, такое, что a+(-a)=0; число a+(-b)=a-b, , называется разно-

стью чисел a и b;

II5. если a<b, то a+с<b+с для любого c R .

3.Операция умножения. Для любой пары вещественных чисел a и b определено такое единственное число, называемое их произведением ab, что выполняются условия:

III1. ab=ba (коммутативность);

III2. a(bc)=(ab)c, a, b, c R (ассоциативность);

III3. существует единственное число 1, называемое единицей, такое, что a1=a для любого a R ;

III4. для любого числа a 0 существует единственное число 1a , называемое ему обратным к данному, такое,

что a 1a =1; число a 1b , b 0 ,называется частным ab от деления a на b;

III5. если либо a, либо b, либо a и b равны 0, то ab=0;

III6. если a<b и c>0, то aс<bс, если a<b и c<0, то aс>bс,

a, b, c R .

4.Дистрибутивность умножения относительно сложения:

(a+b)c=ac+bc для любых a, b, c R .

5.Плотность: для любых a, b R , таких, что a<b, существует такое число c, что a<c<b.

6.Непрерывность: для любых непустых числовых множеств X и Y, таких, что для каждой пары чисел x X и y Y , выполняется неравенство x y , существует число a, удовлетворяющее условию: x a y , x X , y Y .

7

Подмножества множества R.

1.Число 1+1 обозначают 2, число 2+1 обозначают 3 и т.д. Эти числа 1, 2, 3, , образуют множество N

натуральных чисел.

2.Числа, большие 0, называются положительными чис-

лами, числа, меньшие 0 – отрицательными. Числа

0, 1, 2, образуют множество Z целых чисел.

3. Числа, представимые в виде несократимого отношения mn , m Z, n N , образуют множество Q рацио-

нальных чисел.

4.Действительные числа, не являющиеся рациональны-

ми, образуют множество I иррациональных чисел.

5.Множество R является объединением множеств Q и I:

R Q I .

Свойство Архимеда. Каково бы ни было число a R , существует такое число n N , что n>a.

Следствие. Каковы бы ни были числа a и b, 0<a<b, существует такое число n N , что na >b.

Числовые промежутки.

Пусть P(x) – какое-то свойство числа x. Тогда запись

x : P(x) означает множество чисел, обладающих свой-

ством P(x).

Пусть даны два числа a и b, a<b. Рассмотрим следующие множества на числовой оси:

x : a x b - отрезок (сегмент) [a,b];

x : a x b (a;b] , x : a x b [a;b) - полуинтер-

валы;

x : a x b - интервал (a,b);

x : x a или x : x a - полуоси [a, ) или ( ,a].

8

Все указанные множества называются промежутками. Кванторы (логические символы).

(для любого, для каждого) – квантор всеобщности.(существует) – квантор существования.

Ограниченность множеств.

Числовое множество X называется ограниченным сверху (снизу), если c : x X x c x c (если существует число c такое, что для любого x из X выполняется неравенство x c x c ).

Множество, ограниченное сверху и снизу, называется

ограниченным множеством.

Примеры: [2,3] – ограниченное множество;2, - множество, ограниченное снизу;,4 - множество, ограниченное сверху.

Комплексные числа.

Комплексным числом называется выражение вида

z=x+iy, x, y R , i 1 - мнимая единица, то есть число,

квадрат которого равен -1.

x=Re z – действительная часть z. y=Im z – мнимая часть z.

Действительное число x является частным случаем комплексного числа z=x+iy при y=0.

Если x=0, а y 0 , то числа вида z=iy называются мнимыми

числами.

Комплексное число z=x+iy равно 0, если x=0 и y=0.

Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются рав-

ными, если x1= x2 и y1= y2.

Определение. Будем говорить, что между множествами X и Y установлено соответствие, если по какому-либо закону

9

или правилу каждому элементу x X соответствует элемент y Y . Соответствие называется взаимно-однозначным, если любому x X соответствует только один элемент y Y и, наоборот, любому y Y соответствует только один элемент x X .

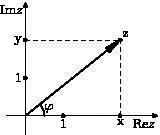
Комплексные числа изображаются точками на комплексной плоскость (см. рис.3.).Плоскость называется комплексной, если каждому комплексному числу z=x+iy ставится в соответствие точка плоскости Z(x,y), причём это соответствие взаимно-однозначное.

Оси Ox и Oy прямоугольной (декартовой) системы координат, на которых расположены действительные числа z=x+0i=x и мнимые числа z=0+iy=iy, называются соответ-

ственно действительной и мнимой осями.

Рис.3. Комплексная плоскость (x,0) – действительное число x;

(0,y) – мнимое число z=iy;

(0,1) – мнимая единица i;

(1,0) – действительное число 1;

(0,0) – z=0;

(x,y) – комплексное число z=x+iy. Все эти числа изображены на рис.3.

10