Методы интегрирования уравнения движения машинного агрегата
Уравнения движения машины решаются, с целью определения истинных значений кинематических и динамических параметров механизма: скоростей, ускорений, времени движения звеньев, сил, действующих в механизмах, итак, мы составили дифференциальное уравнение движения машинного агрегата это уравнение имеет вид для случая вращательного движения звена приведения
или для случая, когда звено приведения движется поступательно:
.
Это уравнение можно применять и для вращающего звена, имея в виду, что V=, Mn=Pnr, Jn=mnr2 . Моменты сил движущих и сил сопротивления, входящие в правую часть уравнения, могут быть функциями обобщенной координаты (положения), скорости и времени.
Например,
для машинного агрегата, представляющего
асинхронный двигатель с вентилятором
и
;
для корабля, где машинный агрегат
представляет двигатель внутреннего
сгорания, передаточный механизм и
гребной винт в качестве исполнительного
органа
,
для кривошипного пресса, где машинный
агрегат представляет электродвигатель
– передаточный механизм
– кривошипно-ползунный механизм в
качестве исполнительного механизма
и
(рисунок 4.24).
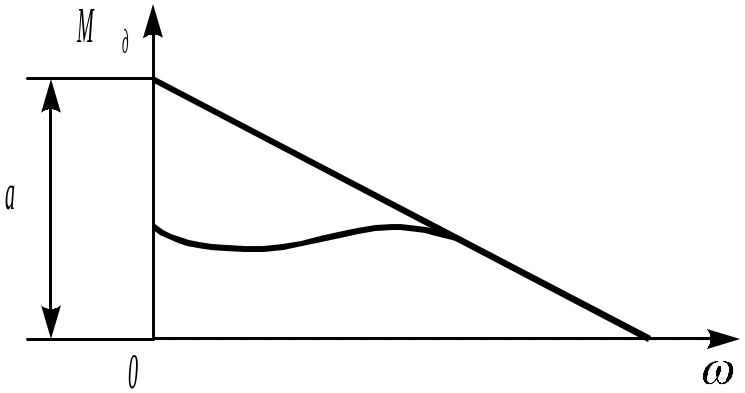
Рисунок 4.73
Обычно эти функции задаются одним из способов: в виде аналитических формул или чаще всего в виде графиков, так называемых механических характеристик. Например, для асинхронного электродвигателя зависимость движущего момента на его валу от скорости может быть представлена следующим образом:
M = a – b.
Запишем уравнения движения рассмотренных примеров:
, (4.31)
где
или функция одной переменной (1–3), или
функции разных переменных (4–6).
Из этих уравнений (4.31) только уравнение 1 может быть решено в квадратурах. Решение в конечном виде зависит от того, насколько сложны подинтегральные выражения. Проделаем эту операцию.
. (4.32)
Интегрирование проводим по частям, имея в виду, что Jn и являются некоторыми функциями .
.
Пусть
,
тогда
;
.
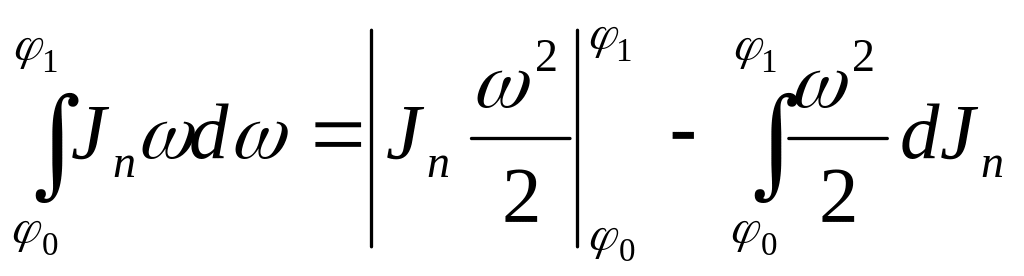Подставляя полученное выражение в исходное уравнение (4.32), получим
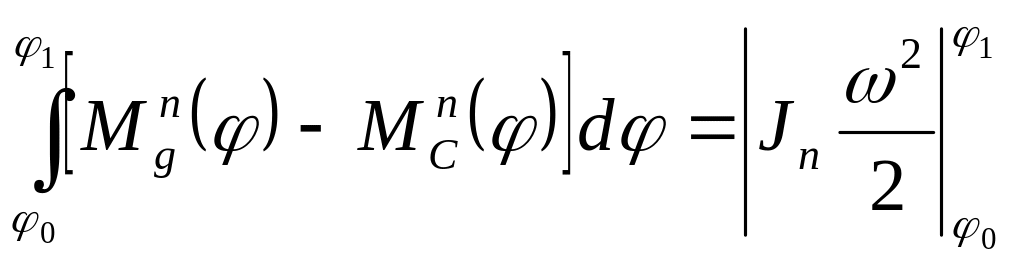
или
. (4.33)
В сокращённой записи уравнение (4.33) будет выглядеть следующим образом:
(4.34)
Это
первый интеграл дифференциального
уравнения движения машины в форме
изменения кинетической энергии. Из
этого уравнения (4.34) при заданном 0
может быть определено i.
Уравнения для случаев 2
и 3 могут быть решены в
квадратурах в частном случае, когда
Jn=const,
т.е.
,
тогда уравнение для 2-го случая
примет вид
. (4.35)
Представляя уравнение (4.35) в квадратурах, получим
. (4.36)
Уравнение движения для 3-го случая при Jn=const приводится к виду
(4.37)
или в квадратурах
. (4.38)
Уравнения движения для случаев 4, 5 и 6 в квадратурах не решаются. Все уравнения движения для случаев 1–6 могут быть проинтегрированы численным методом (например метод Эйлера) путем перехода от дифференциалов к конечным (но малым) разностям и вычислению результатов на малых интервалах поворота или за малые промежутки времени (т.е. вычисления ведутся шаг за шагом и последующий результат не может быть получен без вычисления предыдущего, т.е. вычислить какой-либо параметр в любой момент движения машины можно только после целого ряда вычислений результатов, предшествующих избранному моменту).
Для примера возьмем наиболее типичный случай
(4.39)
и представим это уравнение в виде:
решая его относительно
,
получим
.
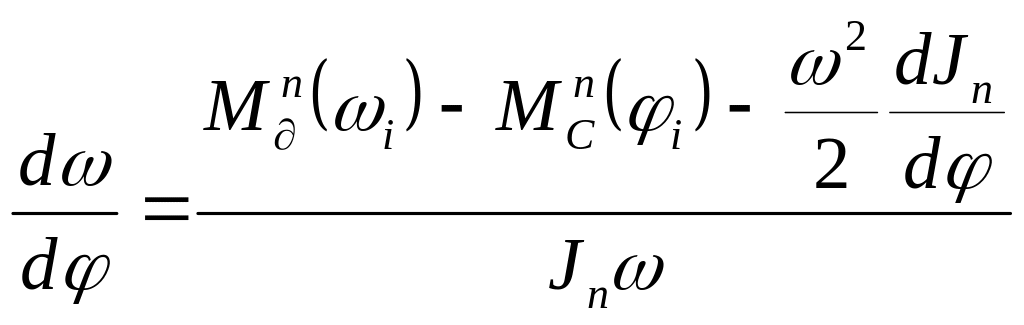Переходя к конечным разностям, получим
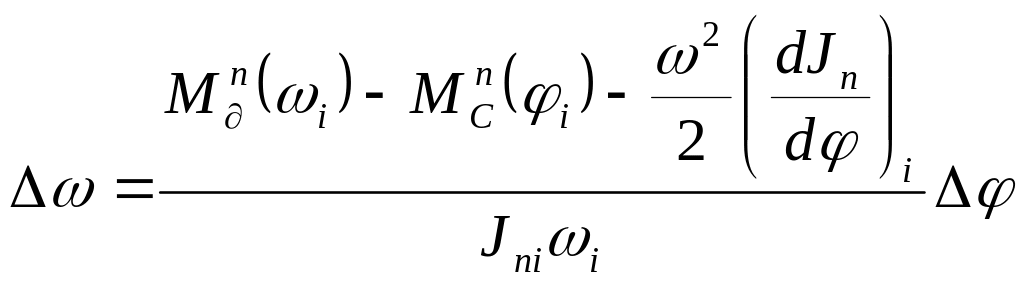. (4.40)
Таким
образом, задавшись шагом интегрирования
, можно построить
скорости звена приведения,
начиная вычисления от заданного
0.
Значения Jn
и dJn
/d
для всех положений звена приведения мы
можем определить с помощью планов
скоростей и ускорений, построенных для
его равномерного движения. На рисунке
4.25 представлен график
.
Значения
определяются по механической характеристике
двигателя. Ускорение звена приведения
может быть определено из уравнения
движения в виде табличных данных или
графическим дифференцированием графика
(),
т. к.
.
Угловые ускорения можно получить и из уравнения движения (4.39):
.
Откуда
.
Все переменные, входящие в эту зависимость, получены в процессе интегрирования (рисунок 4.28).
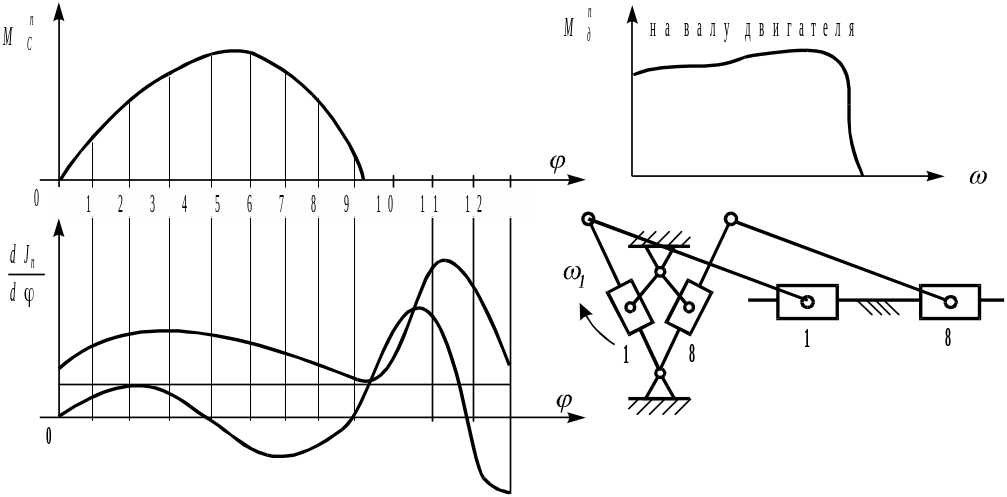
Рисунок 4.74
Более точное решение (4.40) можно получить следующим образом
.
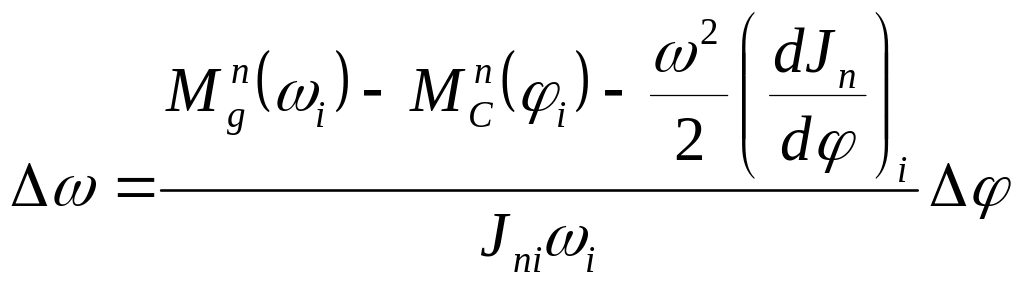Задаёмся значением 0 (0 = ср), тогда:
;
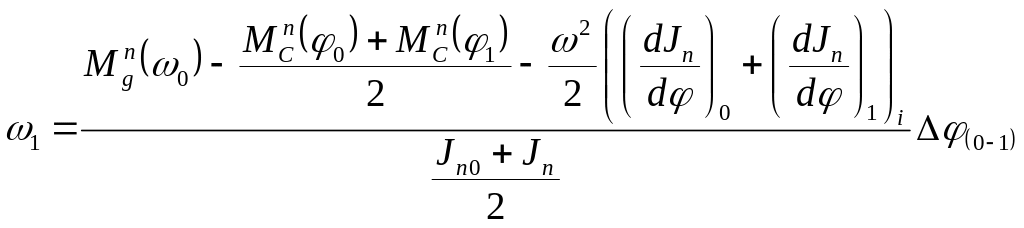Все значения для подстановки в эту формулу берутся из графиков, приведенных на рисунке 4.25.