
- •Часть 4
- •1.Функции нескольких переменных
- •1.1. Понятие функции двух переменных. Область определения
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные и частные дифференциалы первого порядка
- •1.4. Полное приращение функции и полный дифференциал
- •1.5. Применение полного дифференциала в приближенных вычислениях первого порядка
- •1.6. Частные производные сложной функции. Полная производная
- •1.7. Дифференциал сложной функции. Инвариантность формы первого дифференциала
- •1.8. Производная по направлению. Градиент
- •1.9. Частные производные и дифференциалы высших порядков
- •1.10. Дифференцирование функций, заданных неявно
- •1.11. Экстремум функции нескольких переменных. Необходимое условие
- •1.12. Достаточный признак экстремума
- •1.13. Наибольшее и наименьшее значение функции в замкнутой области
- •Вопросы для самопроверки
- •2. Двойной интеграл
- •2.1. Основные понятия и определения
- •2.2. Основные свойства двойного интеграла
- •2.3. Вычисление двойного интеграла в декартовых координатах
- •2.4. Вычисление двойного интеграла в полярных координатах
- •2.5. Вычисление объемов тел с помощью двойного интеграла
- •2.6. Вычисление площадей плоских фигур
- •2.7. Вычисление площадей поверхностей
- •2.8. Моменты инерции плоской фигуры
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3. Тройной интеграл
- •3.1 Задача, приводящая к понятию тройного интеграла
- •3.2. Вычисление тройного интеграла в декартовых координатах
- •3.3. Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
- •3.4. Вычисление объема тела с помощью тройного интеграла
- •3.5. Приложение тройного интеграла для вычисления массы тела
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •4.1. Основные понятия
- •4.2. Вычисление криволинейного интеграла II рода
- •4.3. Формула Грина
- •4.4. Условия независимости криволинейного интеграла II рода от пути интегрирования
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5. Поверхностный интеграл II рода
- •5.1. Основные понятия
- •5.2. Вычисление поверхностного интеграла II рода
- •5.3. Формула Остроградского-Гаусса
- •5.4. Формула Стокса
- •5.5. Векторная запись формулы Стокса. Ротор вектора
- •5.6. Потенциальные векторные поля. Нахождение потенциала
- •5.7. Оператор Гамильтона. Векторные операции второго порядка
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Начала математического анализа
- •Часть 4
- •Подписано к изданию 02.05.06.
- •394026 Воронеж, Московский просп., 14
1.2. Предел и непрерывность функции двух переменных
Определение
функции двух переменных требует введение
определения
- окрестности точки
М.
-
окрестностью точки
M0
(х0,у0)
называется внутренняя часть круга
радиуса
с
центром
в точке
M0
(х0,у0)
или
множество
точек M
(х,у),
удовлетворяющих неравенству
![]()
.
.
Число А называется пределом функции двух переменных f(х, у) при х х0, у у0 , если для любого сколь угодно малого положительного найдется такое > 0, что для всех точек - окрестности точки М0(х0,у0) выполняется неравенство
![]() <
.
<
.
Согласно определению, предел А не зависит от способа приближения точки М к точке М0. В этом случае пишут:
![]() ,
,
![]() .
.
Остаются в силе все теоремы о пределе функции и правила вычисления.
При вычислении предела функции двух переменных вычисляется предел функции f (х, у) по всем возможным прямым, проходящим через точку М0 (при М М0), если все эти пределы равны числу А, то .
Пример
1.
Найти
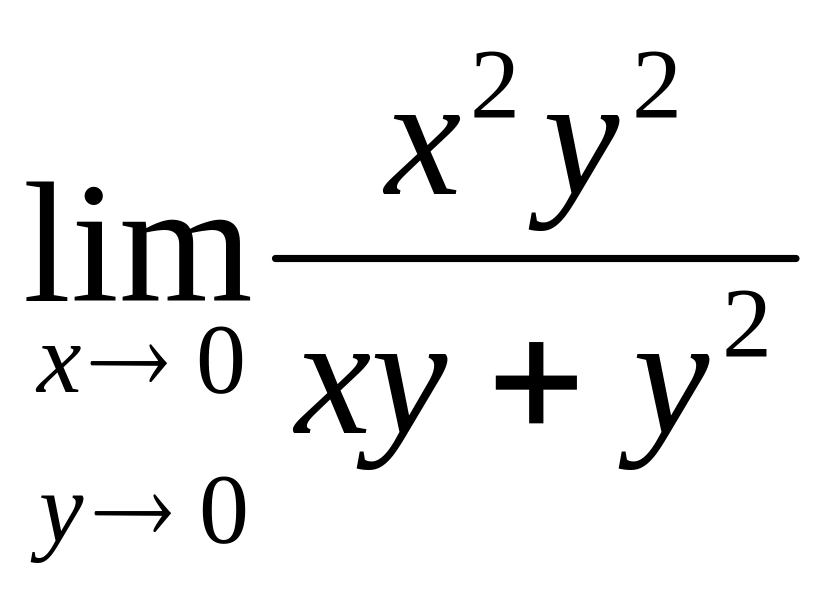 .
.
Решение: Пусть точка М стремится к точке М0 по прямой y=kx. Тогда


 0.
0.
Значение предела не зависит от k , поэтому А=0.
Пример
2.
Найти
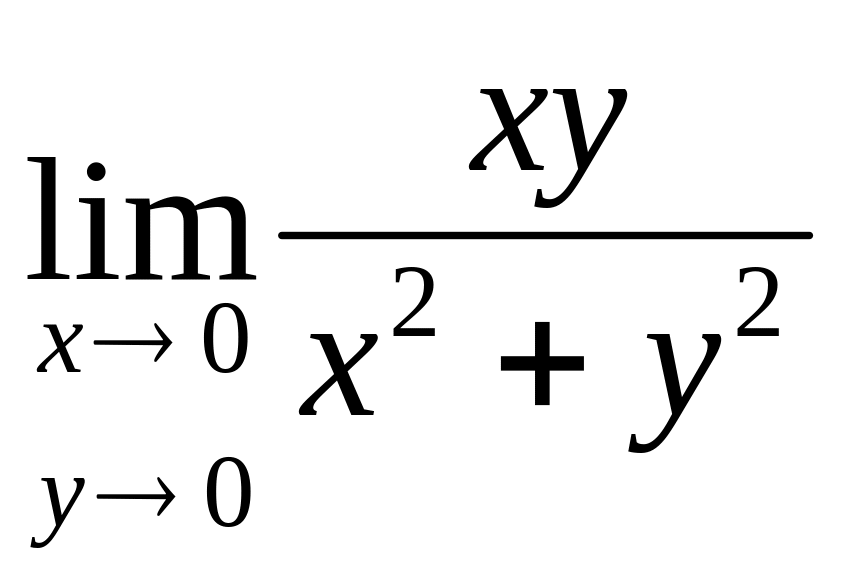 .
.
Решение:

![]()
![]() .
.
Для различных k получаем различные значения предела, что и означает, что в точке О (0,0) функция предела не имеет.
По
аналогии с функцией одной переменной
функция
f(х,у)
называется
бесконечно малой, если
![]() .
.
Функция
f
(х,у) называется
непрерывной в точке М0(х0,у0),
если
![]() .
.
Для выполнения условия непрерывности необходимо, чтобы:
1) функция f (х, у) была определена в точке М0(х0, у0);
2)
существовал предел
![]() ;
;
3) f (М0) = А.
Функция f (х, у) называется непрерывной в области, если она непрерывна в каждой точке этой области.
Точка
М(х,у)
называется
точкой разрыва функции
f(х,у),
если
функция либо не определена в самой
точке, либо не существует предел
![]() ,
либо предел существует, но не равен
значению функции в данной точке. Например,
функция
,
либо предел существует, но не равен
значению функции в данной точке. Например,
функция
![]() имеет точку разрыва М0(0,0).
имеет точку разрыва М0(0,0).
Определение непрерывности функции нескольких переменных f (x,y) совершенно аналогично определению непрерывности функции одной переменной. Поэтому все свойства, установленные для непрерывных функций одной переменной, остаются в силе для непрерывных функций нескольких переменных:
1.Все элементарные функции нескольких переменных непрерывны в области определения.
2.
Если функция f
(x,y)
непрерывна в замкнутой области![]() ,
то она ограничена в ней (достигает
наибольшего и наименьшего значения).
,
то она ограничена в ней (достигает
наибольшего и наименьшего значения).
3. Непрерывная в области D функция, непрерывно переходя от одного своего значения к другому, проходит через каждое промежуточное значение.
Заметим,
что непрерывность функции f
(х,у)
по совокупности
аргументов
не сводится к непрерывности
по каждому аргументу в отдельности.
В примере 2 функция
![]() по каждому из аргументов в отдельности
непрерывна. Например, если М
М0
по оси
Ох (у=0),
то z
0 и
по каждому из аргументов в отдельности
непрерывна. Например, если М
М0
по оси
Ох (у=0),
то z
0 и
![]() .
Аналогично, при стремлении М
М0
по оси Оу
(х=
0)
z
0 и
.
Аналогично, при стремлении М
М0
по оси Оу
(х=
0)
z
0 и
![]() .
.
1.3. Частные производные и частные дифференциалы первого порядка
Пусть
функция z =f
(х, у) определена и непрерывна в
точке М0(х0, у0)
и ее некоторой окрестности. Зафиксируем
значение у = у0, а переменная
х пусть испытает приращение х.
При этом переместимся из точки
![]() в точку
в точку
![]() .
Получим функцию одной переменной z
=f (х, у0).
Разность
.
Получим функцию одной переменной z
=f (х, у0).
Разность
![]()
называется частным приращением функции z по переменной х.
Частной
производной функции
z
по переменной х
в точке М0
(х0,
у0)
называется предел отношения
![]() при
х0
при
х0
![]() =
=![]() =
=![]() =
=![]() .
.
В определении частной производной не все координаты равноправны: переменная у фиксирована, а х изменяется.
При
перемещении из точки М0(х0,у0)
в точку М2(х0,у0+у)
получим частное приращение функции z
по переменной
![]()
![]() .
.
Частной
производной функции
z
по переменной
в точке М0
(х0,
у0)
называется предел отношения
![]() при
при
![]() 0
0
![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
Частные
производные
и
![]() характеризуют мгновенную скорость
изменения функции z
в точке М0
(х0,
у0)
в направлении координатных осей Ох
и
Оу.
характеризуют мгновенную скорость
изменения функции z
в точке М0
(х0,
у0)
в направлении координатных осей Ох
и
Оу.
При вычислении частных производных остаются в силе правила дифференцирования функции одной переменной, а также таблица производных, если другие аргументы считаются постоянными величинами.
Пример
3.
Найти частные производные функции
![]() .
.
Решение:
=![]() ,
=
,
=
![]() Здесь при нахождении
переменная
считается константой, при нахождении
переменная
Здесь при нахождении
переменная
считается константой, при нахождении
переменная
![]() считается константой.
считается константой.
Пример
4. Найти
частные производные функции
![]() .
.
Решение:
![]()
![]() .
.
Рассмотрим геометрический смысл частных производных функции двух переменных. Пусть уравнение z =f(х, у) есть уравнение поверхности, изображенной на рис. 2.
Проведем
плоскость х=
х0
.
В сечении этой плоскостью поверхности
получается линия L2.
При данном х0
рассмотрим на плоскости точку М0.
На поверхности ей соответствует точка
Р.
Частная производная
![]() равна тангенсу угла, образованного
касательной к кривой L2
в точке М
с положительным направлением оси Оу:
равна тангенсу угла, образованного
касательной к кривой L2
в точке М
с положительным направлением оси Оу:
![]() .
.
Для уточнения стоит отметить, что касательная лежит в плоскости х= х0
По
аналогии частная производная![]() численно
равна тангенсу угла наклона касательной
к линии
численно
равна тангенсу угла наклона касательной
к линии
![]() ,
представляющей
сечение поверхности
,
представляющей
сечение поверхности
![]() плоскостью у=у0,
т.е.
плоскостью у=у0,
т.е.![]() .
.

