
- •Часть 4
- •1.Функции нескольких переменных
- •1.1. Понятие функции двух переменных. Область определения
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные и частные дифференциалы первого порядка
- •1.4. Полное приращение функции и полный дифференциал
- •1.5. Применение полного дифференциала в приближенных вычислениях первого порядка
- •1.6. Частные производные сложной функции. Полная производная
- •1.7. Дифференциал сложной функции. Инвариантность формы первого дифференциала
- •1.8. Производная по направлению. Градиент
- •1.9. Частные производные и дифференциалы высших порядков
- •1.10. Дифференцирование функций, заданных неявно
- •1.11. Экстремум функции нескольких переменных. Необходимое условие
- •1.12. Достаточный признак экстремума
- •1.13. Наибольшее и наименьшее значение функции в замкнутой области
- •Вопросы для самопроверки
- •2. Двойной интеграл
- •2.1. Основные понятия и определения
- •2.2. Основные свойства двойного интеграла
- •2.3. Вычисление двойного интеграла в декартовых координатах
- •2.4. Вычисление двойного интеграла в полярных координатах
- •2.5. Вычисление объемов тел с помощью двойного интеграла
- •2.6. Вычисление площадей плоских фигур
- •2.7. Вычисление площадей поверхностей
- •2.8. Моменты инерции плоской фигуры
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3. Тройной интеграл
- •3.1 Задача, приводящая к понятию тройного интеграла
- •3.2. Вычисление тройного интеграла в декартовых координатах
- •3.3. Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
- •3.4. Вычисление объема тела с помощью тройного интеграла
- •3.5. Приложение тройного интеграла для вычисления массы тела
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •4.1. Основные понятия
- •4.2. Вычисление криволинейного интеграла II рода
- •4.3. Формула Грина
- •4.4. Условия независимости криволинейного интеграла II рода от пути интегрирования
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5. Поверхностный интеграл II рода
- •5.1. Основные понятия
- •5.2. Вычисление поверхностного интеграла II рода
- •5.3. Формула Остроградского-Гаусса
- •5.4. Формула Стокса
- •5.5. Векторная запись формулы Стокса. Ротор вектора
- •5.6. Потенциальные векторные поля. Нахождение потенциала
- •5.7. Оператор Гамильтона. Векторные операции второго порядка
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Начала математического анализа
- •Часть 4
- •Подписано к изданию 02.05.06.
- •394026 Воронеж, Московский просп., 14
2.4. Вычисление двойного интеграла в полярных координатах
Пусть в полярной системе координат задана функция z=f(r,φ) в области D, ограниченной линиями:
![]()
![]()
![]() ,
,
![]()
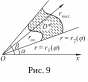
Разобьем
область D
на n
элементарных площадок (Рис 9) с площадями
![]() .
Внутри каждой площадки
выберем точку
.
Внутри каждой площадки
выберем точку
![]() .
Составим интегральную сумму для функции
z=f(r,φ)
в
области D:
.
Составим интегральную сумму для функции
z=f(r,φ)
в
области D:
![]() .
.
Рассмотрим предел полученной интегральной суммы, когда число разбиений неограниченно возрастает. Если этот предел существует, т.е. не зависит от способа разбиения области D на n частей и выбора внутренних точек , то предел называется двойным интегралом функции f(r,φ) по области D
![]()
Для
вычисления полученного интеграла найдем
выражение дифференциала площади
![]() .
Дифференциал
соответствует приращению площади,
возникающему вследствие приращения
полярных координат
.
Дифференциал
соответствует приращению площади,
возникающему вследствие приращения
полярных координат
![]() и
и
![]() .
Площадь фигуры, ограниченной лучами,
выходящими из полюса под углами
.
Площадь фигуры, ограниченной лучами,
выходящими из полюса под углами
![]() и
и
![]() ,
а также дугами окружностей радиусов
,
а также дугами окружностей радиусов
![]() и
и
![]() ,
может быть вычислена как разность
площадей двух круговых секторов
,
может быть вычислена как разность
площадей двух круговых секторов
![]() .
.
Пренебрегая вторым слагаемым как бесконечно малой величиной более высокого порядка малости, для дифференциала площади получим:
![]() .
.
Двойной интеграл в полярных координатах приобретает вид:
![]() .
.
Полученный двойной интеграл вычисляется с помощью соответствующего ему двукратного интеграла

Для
перехода в двойном интеграле
![]() к
полярным координатам. можно также
произвести замену переменных. Переход
от переменных
и
к полярным переменным r
и
φ
осуществляется с
помощью определителя
Якоби или
якобиана
к
полярным координатам. можно также
произвести замену переменных. Переход
от переменных
и
к полярным переменным r
и
φ
осуществляется с
помощью определителя
Якоби или
якобиана
![]() :
:
 .
.
В этом случае справедлива формула:
![]()
Переменные
х
и у
определяются как функции переменных r
и
φ:
x
=![]() ,
y
=
,
y
=![]() .
Якобиан
преобразования
равен
.
Якобиан
преобразования
равен
 .
.
Формула замены переменных в двойном интеграле принимает вид:
![]() .
(1.3)
.
(1.3)
Переход к двукратному интегралу

предполагает возможность описания границ области D посредством уравнений ,
Внутреннее интегрирование производится при постоянном φ.
Пример
17.
Вычислить
![]() ,
где область D
– круг x2
+ y2
≤ 9.
,
где область D
– круг x2
+ y2
≤ 9.
Р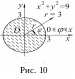 ешение:
Перейдем к полярным координатам: Область
D
в полярной системе координат определяется
неравенствами (рис. 10) 0 ≤ φ
≤ 2π,
0 ≤ r
≤ 3. Переходя к двукратному интегралу
по соответствующей формуле, имеем
ешение:
Перейдем к полярным координатам: Область
D
в полярной системе координат определяется
неравенствами (рис. 10) 0 ≤ φ
≤ 2π,
0 ≤ r
≤ 3. Переходя к двукратному интегралу
по соответствующей формуле, имеем

2.5. Вычисление объемов тел с помощью двойного интеграла
Объем цилиндрического тела, ограниченного боковой цилиндрической поверхностью, поверхностью z = f(x; у) и областью D плоскости xOy находится по формуле
![]() .
.
Пример
18. Найти
объем тела, ограниченного поверхностями
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение: Область , на которую проецируется цилиндроид, изображена на рис. 11.
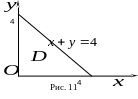
Объему тела соответствует двойной интеграл
![]() .
.
Область
D
может быть описана как правильная
относительно оси
![]() ,
что позволяет перейти к двукратному
интегралу вида
,
что позволяет перейти к двукратному
интегралу вида
![]()
![]()
![]()
Пример
19.
Найти объем тела, ограниченного
поверхностями
![]() и
и
![]() .
.
Решение: Данное тело ограничено сверху и снизу параболоидами, как показано на рис. 12.

Боковая цилиндрическая поверхность выродилась в пространственную линию. Решая систему уравнений
![]()
находим
уравнения вышеуказанной линии:
![]() ,
z
=
2.
,
z
=
2.
Объем
тела равен разности объемов двух
цилиндрических тел с областью
в основании и ограниченных сверху
поверхностями
![]() и
и
![]() Область
определяется неравенством
Область
определяется неравенством
![]() .
.
Учитывая вышесказанное, имеем
![]()
Переходя к полярным координатам, находим:

