Задачи для самостоятельного решения

1. Вычислить криволинейный интеграл второго рода

, где AB- дуга кривой от точки до точки . Ответ: .

2. 1. Вычислить криволинейный интеграл второго рода

, где AB- отрезок прямой от точки до точки . Ответ: .

3. Вычислить криволинейный интеграл второго рода

по дуге эллипса, задаваемого уравнениями , , . Ответ: .

4. . Вычислить криволинейный интеграл второго рода

по кривой , , . Ответ: .

5. Вычислить криволинейный интеграл от выражения, являющегося полным дифференциалом .

Ответ: 8.

6. Вычислить криволинейный интеграл от выражения, являющегося полным дифференциалом .

Ответ: 12.

7. Применяя формулу Грина, вычислить криволинейный интеграл , где - пробегаемый в положительном направлении контур треугольника с вершинами , , . Ответ: .

8. Найти первообразную функцию , если Ответ: .

9. Найти первообразную функцию , если Ответ: .

5. Поверхностный интеграл II рода

5.1. Основные понятия

Пусть – гладкая поверхность, т.е. поверхность в каждой точке имеет касательную плоскость, положение которой непрерывно изменяется вместе с точкой касания.

В произвольной точке М₀ поверхности проведём нормаль, приписав ей одно из двух возможных направлений (рис. 29).

Поверхность называется двусторонней, если для произвольной точки М₀ и любого замкнутого контура L, проходящего через неё и не пересекающего границы поверхности, после обхода контура мы возвращаемся в исходную точку М₀ с исходным направлением нормали.

Если при возвращении в исходную точку направление нормали будет противоположно исходному, то поверхность называется односторонней. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что вершина А совмещается с вершиной С, а, а вершина В – с вершиной D (см. рис. 30). Будут рассматриваться только двусторонние поверхности.

Согласуем направление нормали к двусторонней поверхности с направлением обхода контура L следующим образом: за положительное направление обхода контура L примем направление против часовой стрелки, если смотреть с конца вектора нормали. Направление обхода, обратное положительному, будет считаться отрицательным. Для другой стороны поверхности нормаль изменит своё направление на противоположное. В соответствии с этим придётся изменить направление обхода контура L.

Пусть задана двусторонняя поверхность, и пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x,у,z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части S_i, где i = 1,2,... , n, и проектируем их на координатные плоскости. При этом площадь проекции Δσ_i берем со знаком «плюс», если выбрана верхняя сторона поверхности, т.е. если нормаль к выбранной стороне поверхности составляет с осью Oz острый угол (рис. 31, а), со знаком «минус», если выбрана нижняя сторона поверхности (cosγ_i < 0) ( рис. 31, б). Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.

На каждом участке разбиения поверхности выбирается точка , в которой находится значение . Соответствующая интегральная сумма имеет вид

где Δσ_i=(S_i)_Oxy –площадь проекции S_i на плоскость Оху.

Рассмотрим предел интегральной суммы при стремлении к бесконечности и . Если предел существует и не зависит от способа разбиения поверхности S на части S_i и от выбора точек M_i ,принадлежащих участку поверхности S_i, то данный предел называется поверхностным интегралом II рода (по координатам) от функции f(x,у,z) по переменным x и y по выбранной стороне поверхности и обозначается

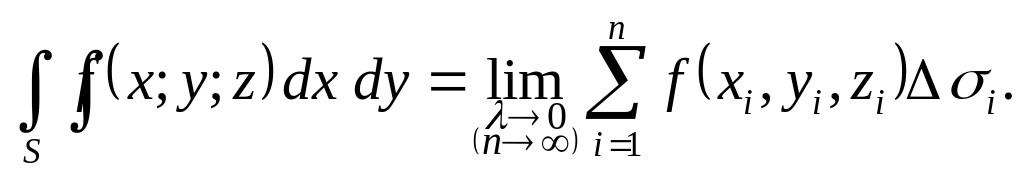
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:

Поверхностный интеграл II рода общего вида представляется следующим образом:

где P, Q, R – непрерывные функции, определенные в точках двусторонней поверхности S.

Применение поверхностных интегралов второго рода в приложениях связано с возможностью интерпретировать поверхностный интеграл как поток векторного поля

через поверхность .

Если поверхность интегрирования S является замкнутой поверхностью, то поверхностный интеграл по внешней стороне ее обозначается а по внутренней -

Перечислим свойства поверхностного интеграла II рода:

1. Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.

2. Постоянный множитель можно выносить за знак поверхностного интеграла.

3. Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.

4. Поверхностный интеграл II рода по всей поверхности S = S₁ + S₂ равен сумме интегралов по ее частям S₁ и S₂ (аддитивное свойство), если S₁ и S₂ пересекаются лишь по границе, их разделяющей.

5. Если S₁, S₂, S₃ – цилиндрические поверхности с образующими, параллельными соответственно осям Oz; Ox; Oy, то