3.4. Вычисление объема тела с помощью тройного интеграла
Объем
области V
выражается формулой
или
-
в
декартовых координатах,
-
в
цилиндрических координатах,
ρ2-в
сферических координатах.
Пример 28. Найти объем тела, ограниченного поверхностями z = х2 + у2 и z = 1.
Решение: Данное тело ограничено сверху плоскостью z = 1, снизу - параболоидом z = x2 + у2 (рис. 21). Объем тела находим, используя цилиндрические координаты:
3.5. Приложение тройного интеграла для вычисления массы тела
Масса тела m при заданной объемной плотности γ вычисляется с помощью тройного интеграла как
где γ(x; y; z) - объемная плотность распределения массы по области .
Пример
29.
Найти массу шара, ограниченного
поверхностью
(
рис. 22),
если плотность в каждой точке равна
.
Решение:
Уравнение сферы
преобразуется к виду
,
ρ2
=
2R
cos
θ.
Вопросы для самопроверки
1. Что является достаточным условием существования тройного интеграла?
2. Перечислите свойства тройного интеграла.
3. Что называется областью, правильной относительно оси ?
4.
Чем определяются пределы интегрирования
во внутреннем интеграле по
для области, правильной относительно
оси
?
5. Как записывается якобиан преобразования при переходе к цилиндрическим координатам?
6. Каким образом описывается положение точки в сферических координатах?
7. Запишите якобиан преобразования при переходе к сферическим координатам?
8. Запишите формулу вычисления массы тела с помощью тройного интеграла.
Задачи для самостоятельного решения
1.
Вычислить тройной интеграл
,
если область интегрирования
ограничена
плоскостями
,
.
Ответ:
.
2.
Вычислить трехкратный интеграл
.
Ответ:
.
3.
Вычислить объем тела, ограниченного
поверхностями:
и
.
Ответ:
.
4.
Вычислить объем тела, ограниченного
поверхностями:
и
(внутри
конуса).
Ответ:
.
5. Определить массу тела, соответствующего области , ограниченной поверхностями , , если плотность масс в каждой точке равна аппликате .
Ответ:
.
6.
. Определить массу тела, соответствующего
области
,
ограниченной поверхностями
,
(
>0),
если плотность масс в каждой точке равна
ординате
.
Ответ:
.
4. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ II РОДА
4.1. Основные понятия
Решение задачи о вычислении работы переменной силы при перемещении материальной точки вдоль кривой приводит к понятию криволинейного интеграла II рода.
Пусть
в плоскости Оху
задана непрерывная кривая
(или АВ)
и функция Р(х,у),
определенная в каждой точке кривой.
Разобьем кривую АВ
точками
=A,
M1,
,...,
Mn=В
в
направлении от точки А
к
точке
B
на n
частей.
На
каждой «элементарной дуге»
выберем внутреннюю точку
и составим интегральную сумму вида
где Δxi = xi-xi-1 - проекция дуги Mi-1 Mi на ось Ox (рис. 23).
Сумму
называют
интегральной суммой для функции Р(х,у)
по
переменной х.
Рассмотрим предел интегральной суммы
,
при
.
Если предел существует, т.е. не зависит
ни от способа разбиения кривой АВ,
ни от выбора точек
,
то его называют криволинейным
интегралом по координате
х (или
II
рода) от
функции Р(х;у) по кривой
АВ и
обозначают
=
=
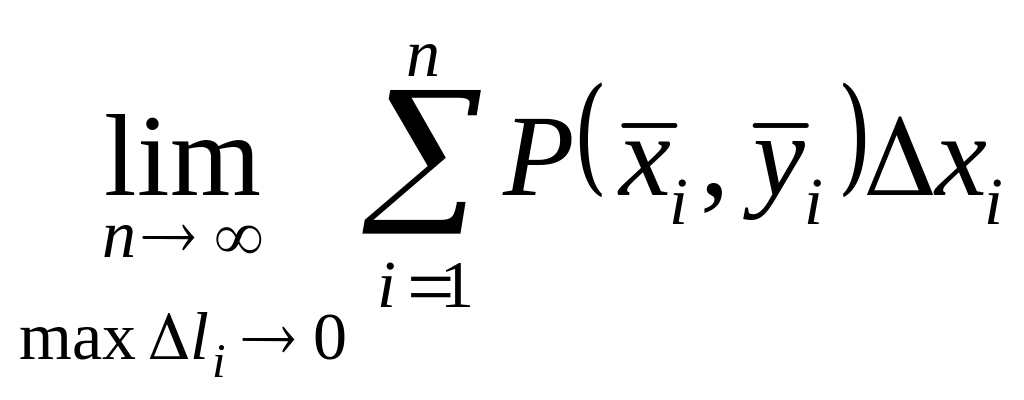По аналогии вводится криволинейный интеграл от функции Q(x; у) по координате у:
где Δyi - проекция дуги Mi-1 Mi на ось Oy.
Криволинейный интеграл II рода общего вида определяется равенством
Кривая L может быть замкнутой. В этом случае говорят о криволинейном интеграле по замкнутому контуру, который обозначают:
.
Теорема о существовании криволинейного интеграла: Если кривая АВ гладкая, а функции Р(х;у) и Q(x;y) непрерывные на кривой АВ, то криволинейный интеграл II рода существует.
Для пространственной кривой может быть определен криволинейный интеграл второго рода вида
.
Отметим свойства криволинейного интеграла II рода.
1. При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т. е.
2. Если кривая АВ точкой С разбита на две части АС и СВ, то интеграл по всей кривой равен сумме интегралов по ее частям, т. е.
=
.
3.
Если кривая АВ
лежит
в плоскости, перпендикулярной оси Ох,
то
.
Если
кривая АВ
лежит
в плоскости, перпендикулярной оси Оy,
то
.
4. Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки, а зависит только от направления обхода кривой (рис. 24):
