
- •Часть 4
- •1.Функции нескольких переменных
- •1.1. Понятие функции двух переменных. Область определения
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные и частные дифференциалы первого порядка
- •1.4. Полное приращение функции и полный дифференциал
- •1.5. Применение полного дифференциала в приближенных вычислениях первого порядка
- •1.6. Частные производные сложной функции. Полная производная
- •1.7. Дифференциал сложной функции. Инвариантность формы первого дифференциала
- •1.8. Производная по направлению. Градиент
- •1.9. Частные производные и дифференциалы высших порядков
- •1.10. Дифференцирование функций, заданных неявно
- •1.11. Экстремум функции нескольких переменных. Необходимое условие
- •1.12. Достаточный признак экстремума
- •1.13. Наибольшее и наименьшее значение функции в замкнутой области
- •Вопросы для самопроверки
- •2. Двойной интеграл
- •2.1. Основные понятия и определения
- •2.2. Основные свойства двойного интеграла
- •2.3. Вычисление двойного интеграла в декартовых координатах
- •2.4. Вычисление двойного интеграла в полярных координатах
- •2.5. Вычисление объемов тел с помощью двойного интеграла
- •2.6. Вычисление площадей плоских фигур
- •2.7. Вычисление площадей поверхностей
- •2.8. Моменты инерции плоской фигуры
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3. Тройной интеграл
- •3.1 Задача, приводящая к понятию тройного интеграла
- •3.2. Вычисление тройного интеграла в декартовых координатах
- •3.3. Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
- •3.4. Вычисление объема тела с помощью тройного интеграла
- •3.5. Приложение тройного интеграла для вычисления массы тела
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •4.1. Основные понятия
- •4.2. Вычисление криволинейного интеграла II рода
- •4.3. Формула Грина
- •4.4. Условия независимости криволинейного интеграла II рода от пути интегрирования
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5. Поверхностный интеграл II рода
- •5.1. Основные понятия
- •5.2. Вычисление поверхностного интеграла II рода
- •5.3. Формула Остроградского-Гаусса
- •5.4. Формула Стокса
- •5.5. Векторная запись формулы Стокса. Ротор вектора
- •5.6. Потенциальные векторные поля. Нахождение потенциала
- •5.7. Оператор Гамильтона. Векторные операции второго порядка
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Начала математического анализа
- •Часть 4
- •Подписано к изданию 02.05.06.
- •394026 Воронеж, Московский просп., 14
4.4. Условия независимости криволинейного интеграла II рода от пути интегрирования
Пусть
![]() и
и
![]() – две произвольные точки односвязной
области D
плоскости. Оху
(область D называется односвязной, если
для любого замкнутого контура, лежащего
в этой области, ограниченная им часть
плоскости целиком принадлежит D
(область без «дыр»)). Точки A
и В
(рис. 27) можно соединить различными
линиями, например, L1,
L2
и L3.
– две произвольные точки односвязной
области D
плоскости. Оху
(область D называется односвязной, если
для любого замкнутого контура, лежащего
в этой области, ограниченная им часть
плоскости целиком принадлежит D
(область без «дыр»)). Точки A
и В
(рис. 27) можно соединить различными
линиями, например, L1,
L2
и L3.

Если по каждой из этих кривых интеграл
![]()
имеет одинаковые значения, то говорят, что интеграл I не зависит от пути интегрирования. В этом случае значение интеграла I зависит от начальной точки и конечной точки пути, что отражается при записи:
![]()
Рассмотрим условия, при которых криволинейный интеграл II рода не зависел от пути интегрирования?
Теорема.
Для того чтобы криволинейный интеграл
![]() не зависел от пути интегрирования в
односвязной области D,
в которой функции P(x,y),
Q(x,y)
непрерывны вместе со своими частными
производными, необходимо и достаточно,
чтобы в каждой точке этой области
выполнялось условие
не зависел от пути интегрирования в
односвязной области D,
в которой функции P(x,y),
Q(x,y)
непрерывны вместе со своими частными
производными, необходимо и достаточно,
чтобы в каждой точке этой области
выполнялось условие
![]() .
.
Доказательство. Рассмотрим произвольный замкнутый контур AmBnA (или L) в области D (рис. 28). Для него имеет место формула Грина
![]()
![]() .
.
В силу условия
имеем:
силу условия
имеем:
![]() или
или
![]()
Учитывая свойства криволинейного интеграла, имеем:
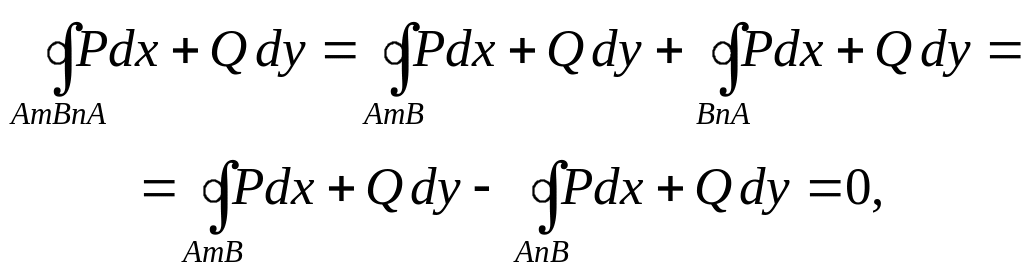
то есть
![]()
Полученное
равенство означает, что криволинейный
интеграл не зависит от пути интегрирования,
что если выполняется условие
![]() .
.
Верно и обратное утверждение.
Если выполнено условие , то подынтегральное выражение P(x; y)dx +Q(x; y)dy является полным дифференциалом некоторой функции u=u(х,у):
P(x,y)dx +Q(x,y)dy=dU(x,y)
Тогда:

![]() ,
,
то есть
 .
.
Полученная формула называется обобщенной формулой Ньютона – Лейбница для криволинейного интеграла от полного дифференциала.
Таким
образом, если подынтегральное выражение
Pdx+Qdy
есть
полный дифференциал
и контур интегрирования L
замкнутый,
то
![]()
Следует отметить, что функцию U = U(x,y), удовлетворяющую условию , можно найти, используя формулу

В качестве начальной точки (х0; у0) обычно берут точку О(0;0).
Пример
35.
Найти

Решение:
Здесь P
= y,
Q
= x,
![]() Согласно вышеприведенной теореме,
интеграл не зависит от пути интегрирования.
В качестве пути интегрирования можно
взять отрезок прямой у
= х,
дугу параболы у=x3
и
т. д. или воспользоваться формулой
.
Так как ydx+xdy
=d(xy),
то
Согласно вышеприведенной теореме,
интеграл не зависит от пути интегрирования.
В качестве пути интегрирования можно
взять отрезок прямой у
= х,
дугу параболы у=x3
и
т. д. или воспользоваться формулой
.
Так как ydx+xdy
=d(xy),
то

Пример 36. Убедиться, что выражение
![]()
представляет собой полный дифференциал некоторой функции U(x; у) и найти ее.
Решение: Для того чтобы указанное выражение являлось полным дифференциалом, необходимо выполнение условий :
![]()
![]() .
.
Отсюда
следует, что
![]() =
=
![]()
Воспользовавшись формулой

имеем:

Вопросы для самопроверки
1. Дайте определение криволинейного интеграла второго рода.
2. Сформулируйте теорему о существовании криволинейного интеграла второго рода.
3. Что изменится, если в криволинейном интеграле поменять местами начало и конец контура интегрирования?
4. Перечислите свойства криволинейного интеграла второго рода.
5. Напишите формулу для вычисления криволинейного интеграла второго рода в случае параметрического задания контура.
6. Что связывает формула Грина?
7. Каким образом определяется положительное направление обхода замкнутого контура?
8. Напишите формулу Грина.
9. Какая область называется односвязной?
10. Докажите теорему о независимости криволинейного интеграла второго рода от пути интегрирования.
11. Когда можно использовать обобщенную формулу Ньютона-Лейбница для криволинейного интеграла?
12.
Как находится функция
![]() с помощью интегрирования?
с помощью интегрирования?
