5.4. Формула Стокса

Обобщением формулы Грина является формула Стокса. Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.

Теорема Стокса. Если функции P(x; y; z), Q(x; y; z) и R(x; y; z) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула

где L является границей поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).

Пусть z =f(x,у) – уравнение поверхности S, функции f(x,у), f_x'(x,y), f_y'(х,y) непрерывны в замкнутой области D, представляющей собой проекцию поверхности S на плоскость Оху, L₁ – граница области D.

Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке (рис. 35). Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл .

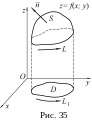
Значения функции Р(х,у,z) на L равны значениям функции Р(х,у,z(x,у)) на границе L₁. Интегральные суммы для криволинейных интегралов II рода по контурам L и L₁ совпадают. Поэтому от интегрирования по контуру L можно перейти к интегрированию по контуру L₁ с помощью формулы

Применяя к этому интегралу формулу Грина, получим:

Полученный двойной интеграл можно преобразовать в равный ему поверхностный интеграл II рода. Для этого последнее равенство перепишем в виде

.

Нормаль имеет проекции . Направляющие косинусы пропорциональны соответствующим проекциям:

Отсюда Тогда

Следовательно,

По аналогии получаются еще два равенства:

После сложения последних трех равенств получаем формулу Стокса.

Следует отметить, что формулу Стокса можно применить для поверхностей более сложного вида, для чего достаточно разбить ее на части рассмотренного выше типа.

Формулу Стокса можно применять для вычисления интеграла по замкнутому контуру с помощью поверхностного интеграла.

Из формулы Стокса вытекает, что если выполняются условия

,

то криволинейный интеграл по произвольному пространственному замкнутому контуру L равен нулю:

что означает независимость криволинейный интеграл от пути интегрирования.

Пример 34. Вычислить , где контур L представляет собой окружность : а) непосредственно, б) используя формул Стокса, взяв в качестве поверхности полусферу

Решение: Поверхность интегрирования изображена на рисунке 36.

а) Запишем уравнение окружности в параметрической форме:

П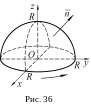 о формуле перехода к определенному интегралу для параметрически заданной кривой имеем:

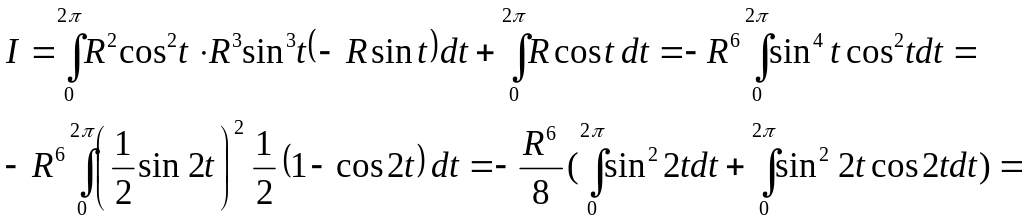
б) По формуле Стокса находим:

Переходя к полярным координатам, получаем:

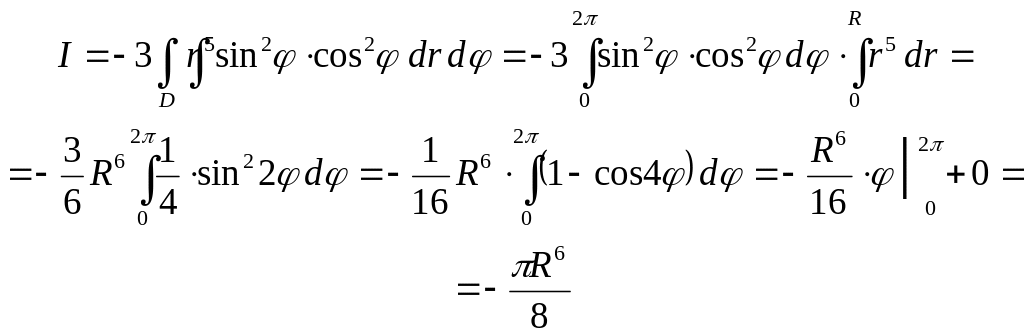
5.5. Векторная запись формулы Стокса. Ротор вектора

Формула Стокса может быть записана в очень компактной формуле при использовании векторных обозначений. Левая часть формулы представляет собой циркуляцию векторного поля :

.

Для преобразования правой части формулы введем новый вектор – ротор или вихрь:

.

Пусть - единичный вектор нормали к выбранной стороне поверхности. Тогда подынтегральная функция в правой части формулы Стокса есть скалярное произведение . Формула Стокса может быть переписана в виде:

.

Левая часть формулы представляет собой циркуляцию вектора вдоль контура , а правая часть – поток через поверхность , натянутую на контур .

Согласно формуле Стокса циркуляция векторного поля вдоль любого замкнутого контура равна потоку ротора этого поля через поверхность, опирающуюся на этот контур. Направление обхода контура должно быть согласовано с выбором стороны поверхности.

Ротор вектора удобно записывать символично формулой: .

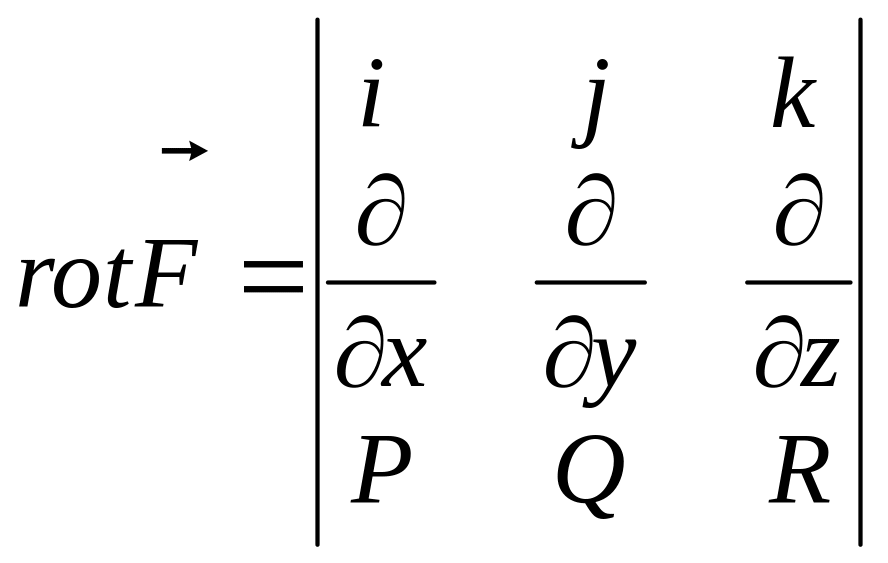Отметим некоторые свойства ротора.

1. Ротор постоянного вектора равен нулю ( ).

2. , где с-константа.

3. , т.е. ротор суммы двух векторов равен сумме роторов этих векторов.

4. Если скалярная функция, вектор, то .

Следует отметить, что характеризует вращательную компоненту вектор - функции.