
- •Введение
- •1. Общие понятия об управлении
- •1.1. Разновидности и свойства сар
- •1.2. Законы регулирования
- •1.3. Задачи тау, классификация сау, примеры
- •1.4. Классификация сау
- •1.4.1. Оптимальные системы автоматического управления
- •1.4.2. Квазиоптимальные сау
- •1.4.3. Общие понятия и классификация
- •1.4.4. Самонастраивающиеся сау со стабилизацией критерия качества управления
- •1.4.5. Самонастраивающиеся сау с оптимизацией качества управления
- •1.4.6. Методы исследования и расчет самонастраивающихся сау
- •1.5. Математические модели объектов и систем управления
- •1.5.1. Общие замечания по объектам
- •1.6. Принципы построения систем автоматического управления
- •1.6.1. Принцип возмущения или регулирование по возмущению
- •1.6.2. Принцип отклонения или регулирование по отклонению (принцип обратной связи)
- •1.6.3. Принцип дуального управления или принцип
- •1.7. Примеры сау
- •2. Линейная теория автоматического управления
- •2.1. Классификация линейных систем
- •2.2. Линеаризация нелинейных функций
- •3. Характеристики сар и типовых
- •3.1 Временные характеристики сар
- •3.2. Частотные характеристики сар
- •3.3. Разновидность типовых звеньев сар
- •4. Устойчивость и качество сар
- •4.1. Основные условия устойчивости
- •4.2. Критерии устойчивости линейных сау
- •4.3. Алгебраический критерий устойчивости
- •4.4. Частотный критерий устойчивости Михайлова
- •4.5. Частотный критерий устойчивости Найквиста
- •4.6. Оценки качества регулирования
- •4.7. Оценка качества регулирования по косвенным критериям
- •5. Анализ и синтез сау
- •5.1. Корневой метод синтеза
- •5.2. Метод корневых годографов
- •6.Системыавтоматического управления с цифровыми вычислительными машинами
- •6.1. Процессы, протекающие в системах цу
- •6.2. Особенности динамики цифровых сау
- •6.3. Методы исследования цифровых сау
- •7.Особенности математического описания цифровых систем управления
- •7.1. Правила эквивалентных преобразований структурных схем систем автоматического управления
- •7.1.1. Принцип суперпозиции (наложения)
- •7.2. Понятие многомерной системы
- •7.3. Методы оценки качества систем управления
- •7.4. Оценка качества при гармонических
- •7.4.1. Интегральные оценки качества
- •7.5. Определения и задачи идентификации
- •Заключение
- •Библиографический список
- •394026 Воронеж, Московский просп., 14
1.4.1. Оптимальные системы автоматического управления
Системы, в которых обеспечено оптимальное значение какого-либо основного показателя качества работы системы - критерия оптимальности, называется оптимальными САУ.
В качестве критерия эффективности оптимальных САУ может быть: один из показателей качества переходного процесса, точность в установившихся режимах, потребляемая мощность, себестоимость продукции и т.п.
Примеры оптимальных САУ:
- СУ полетом самолета, обеспечивающая минимальный расход горючего на заданном маршруте.
- СУ курсом корабля, осуществляющая максимально быстрое изменение курса при наличии ограничений угла поворота и скорости перекидки руля.
Рассмотрим методику синтеза оптимальной САУ.
Наиболее важной
задачей при осуществлении синтеза,
является получение количественного
критерия оптимальности. Критерий
оптимальности, как правило, является
функционалом (функционал - это величина,
значение которой определяется заданием
функции. Например, интегральные критерии
качества в линейных САУ определяются
всей кривой ПП, т.е. функцией
![]() ).
).
Если критерий оптимальности найден, то задача синтеза оптимальной САУ сводится к синтезу устройства управления, обеспечивающего минимум (максимум) выбранного критерия оптимальности.
Формулировка математической постановки задачи синтеза оптимального УУ:
Имеется ОУ, выходная величина которого описывается зависимостью
|
|
где ![]() - управляющее воздействие,
- управляющее воздействие,
![]() - внешнее возмущение.
- внешнее возмущение.
В общем случае
![]() – векторы, содержащие произвольное
число составляющих, а
– векторы, содержащие произвольное
число составляющих, а
![]() – оператор ОУ, в общем случае нелинейный.
Время
– оператор ОУ, в общем случае нелинейный.
Время
![]() – присутствует в (1.5), если объект
нестационарный.
– присутствует в (1.5), если объект
нестационарный.
Зависимость (1.5) для САУ обычно имеет вид системы дифференциальных уравнений:
|
где
![]() - в общем случае нелинейные функции.
- в общем случае нелинейные функции.
Система (6.2) перепишется в векторной форме, как
|
|
где
![]() -
-
![]() -мерный
вектор.
-мерный
вектор.
В реальных условиях
на управляющие воздействия
и на координаты объекта
![]() накладываются различного рода ограничения.
Такими ограничениями, например, являются:
насыщение в УУ, ограничение скорости,
угловых расстояний и т.п. Эти ограничения
можно выразить следующими неравенствами:
накладываются различного рода ограничения.
Такими ограничениями, например, являются:
насыщение в УУ, ограничение скорости,
угловых расстояний и т.п. Эти ограничения
можно выразить следующими неравенствами:
|
|
где
![]() – функции или функционалы.
– функции или функционалы.
В простейшем случае ограничение величины отдельной координаты, неравенство (1.8) принимает вид
|
|
где
![]() - предельно допустимые значения
соответствующих координат.
- предельно допустимые значения
соответствующих координат.
В самом общем
случае критерий оптимальности зависит
как от
![]() и
,
так и от задающего воздействия
и
,
так и от задающего воздействия
![]() ,
обычно он представляет интегральную
зависимость:
,
обычно он представляет интегральную
зависимость:
|
|
где
![]() - длительность всего
процесса.
- длительность всего
процесса.
Зависимостями
вида (1.9), в частности, являются интегральные
критерии качества ПП и среднеквадратичное
отклонение случайных процессов. В
простейшем, но важном случае, когда
![]() ,
критерий оптимальности принимает вид
,
критерий оптимальности принимает вид
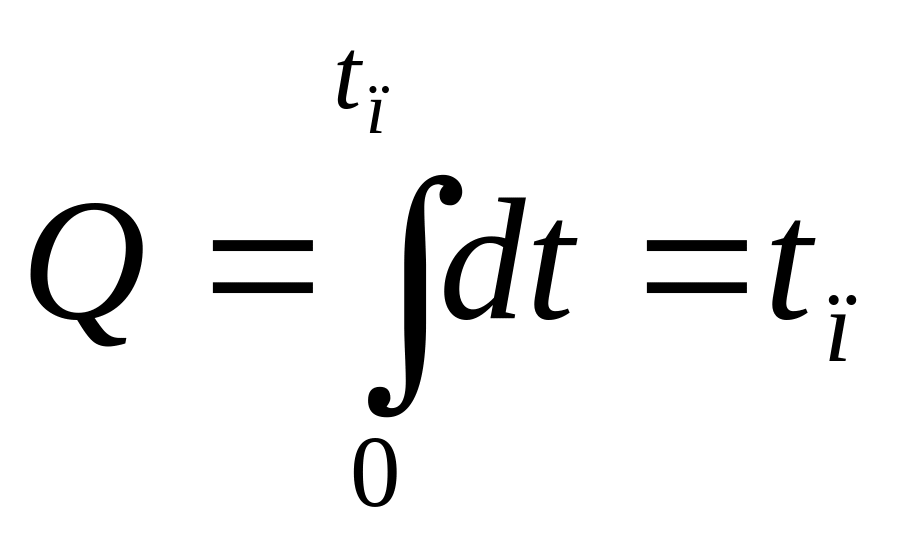 ,
(1.10)
,
(1.10)
т.е. минимизируется время процесса управления, такие САУ называются оптимальными по быстродействию.
Итак, задача
получения оптимального управления
![]() ,
при котором обеспечивается минимум
функционала
,
при котором обеспечивается минимум
функционала
![]() и выполняются условия - ограничения .
и выполняются условия - ограничения .
Задача оптимального управления, в которой заданы начальные и конечные точки траектории называется задачей с фиксированными концами.
Следует отметить,
что определение оптимального управления
и самого процесса
![]() не завершает решение задачи синтеза
САУ.
не завершает решение задачи синтеза
САУ.
Конечной целью
синтеза является определение оператора
УУ -
![]()
|
|
Если одно из внешних
воздействий
![]() или
является случайным, то критерий
оптимальности будет статистическим,
отсюда, при синтезе оптимальных САУ
различают две группы синтеза:
или
является случайным, то критерий
оптимальности будет статистическим,
отсюда, при синтезе оптимальных САУ
различают две группы синтеза:
- Оптимальные САУ, находящиеся под воздействием детерминированных сигналов;
- Оптимальные САУ, находящиеся под случайными воздействиями.

 (1.6)
(1.6)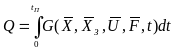 ,
(1.9)
,
(1.9)