51 Вопрос

Теорема Шеннона

1) Для любого префиксного кодирования f и любого источника сообщений hA, Pi избыточность неотрицательна, т. е. Rn(f , P) ≥ 0.

2) Для любого источника сообщений hA, Pi найдётся такое префиксное кодирование f , что r(f , P) = 0.

Доказательство.

Из определений, неравенства Йенсена для функции log t и неравенства Крафта — Макмиллана для произвольного префиксного кодирования f имеем

−Rn(f , P) = X |w|=n P(w)log 1 P(w) − X |w|=n |f (w)|P(w) = = X |w|=n P(w)log 2 −|f (w)| P(w) ≤ X |w|=n log 2−|f (w)| ≤ log 1 = 0

Для любого слова w ∈ A n определим lw = dlog 1 P(w) e. Имеем

X |w|=n 2 −lw ≤ X |w|=n P(w) = 1.

Из неравенства Крафта — Макмиллана следует, что найдётся префиксное кодирование fn : A n → {0, 1} ∗ с длинами кодовых слов |fn(w)| = lw . Определим кодирование f равенством f (w) = 2Bin(|w|)f|w|(w). Cлово f (u) не может быть префиксом f (v) при |u| 6= |v|, из-за того, что 2Bin — префиксное кодирование натурального ряда, а при |u| = |v| = n и u 6= v, из-за того, что fn — префиксное кодирование A n .

|f (w)| = log 1 P(w) + |2Bin(w)| ≤ log 1 P(w) + 2 log |w| + 2, Rn(f , P) ≤ X |w|=n P(w) log 1 P(w) + 2 log |w| + 2 − X |w|=n P(w)log 1 P(w) = X |w|=n P(w)(2 log n + 2)

2Bin(n) = 0 . . . 0 Bin(n)

Следующее кодирование множества N ∪ {0} было предложено В. И. Левенштейном. Введем обозначение λ(n) = |Bin0 (n)| и λ k (n) = λ(λ k−1 (n)), где λ 1 (n) = λ(n). Если λ k (n) = 0 и λ k−1 (n) > 0, то определим

Lev(n) = 1 . . . 1 0Bin0 (λ k−2 (n)). . . Bin0 (λ(n))Bin0 (n)

Кодирование Шеннона

Пронумеруем буквы алфавита так, чтобы P(a1) ≥ P(a2)· · · ≥ P(ak ) > 0. Определим числа σi рекуррентно: σ1 = 0, σi+1 = σi + P(ai) при 1 ≤ i ≤ k. Ясно, что 0 ≤ σi < 1 для любого i = 1, . . . , k. В качестве кодового слова fSh(ai) возьмем dlog 1 P(ai ) e первых после запятой символов в позиционной двоичной записи числа σi .

1) Кодирование Шеннона fSh — префиксное.

2) R1(fSh, P) ≤ 1 для любого источника сообщений hA, Pi.

Доказательство.

Из определения позиционной двоичной записи числа следует, что n первых после запятой двоичных знаков чисел a и b (1 > a > b > 0) совпадают, если и только если a − b < 2 −n . Пусть j > i, тогда

σj − σi ≥ P(ai) = 2 − log(1/P(ai )) ≥ 2 −dlog(1/P(ai ))e = 2 −|fSh(ai )|

Таким образом, первые после запятой |fSh(ai)| символов в двоичной записи числа σj не совпадают с кодовым словом fSh(ai). Поскольку P(aj) ≤ P(ai), имеем |fSh(aj)| ≥ |fSh(ai)|, и префиксность множества fSh(A) доказана.

52 Вопрос

Рассмотрим системы, в которых передача непрерывных сообщений сводится к передаче чисел (кодовых групп), отображающих дискретные (квантованные) уровни сообщения в моменты отсчета на шкале времени. К таким системам, в частности, относятся импульоно-кодовая модуляция и дельта-модуляция.

В системе ИКМ сигнал представляет собой последовательность кодовых комбинаций, отображающих квантованные по уровню значения передаваемого сообщения u(t).

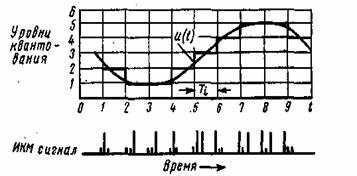
Преобразование непрерывного сообщения в трехзначный ИКМ сигнал

Если взять трехзначный код, то можно составить комбинации, приведенные в таблице

Кодовые комбинации представляют собой числа, записанные в двоичной системе. В этой системе разряды соответствуют числам 1, 2, 4, 8 и т. д.

Период следования комбинаций выбирается равным периоду отсчетов мгновенных значений   колебания u(t). Каждая кодовая комбинация содержит k элементарных посылок одинаковой длительности. В общем случае эти посылки могут принимать т значений. Это позволяет кодировать и передавать L=m^k уровней колебания u(t). Скорость передачи при этом будет равна:

                                                                                                                 

где   частота отсчетов.

При p = 2Fm                                                                                                     

Для двоичного кодирования, которое мы и будем рассматривать в дальнейшем, m=2 и

R=2kFm                                                                                                            

Для передачи посылок кодовых комбинаций может быть использован любой из способов передачи дискретных сигналов, рассмотренных в предыдущей главе (AM, ЧМ, ФМ).

В приемнике кодовые группы декодируются и образуют последовательность импульсов, пропорциональных переданным отсчетам. В простейшем случае это достигается тем, что кодовые комбинации передаются в обратном порядке, т.е. сначала низшие, а затем высшие разряды. Импульсы подаются на RС-цепочку с такой постоянной времени, чтобы разряд убывал в m раз за время между импульсами.

После последнего импульса накопленный заряд (напряжение) снимается. Так получается импульс, соответствующий одному отсчету. Аналогично будут получены другие импульсы. Затем эти импульсы пропускаются через фильтр нижних частот с граничной частотой Fm для восстановления переданного сообщения u(t).

Особенностью ИКМ, так же как и других систем с квантованием, является то, что даже при полном отсутствии помех в канале принятое сообщение v(t) отличается от передаваемого u(t), поскольку квантованное сообщение лишь приблизительно совпадает с исходным. Поэтому при отсутствии помех

v(t)=u(t)+ε(t)

где ε (t) представляет собой так называемый «шум квантования». Легко видеть, что значение случайной функции ε находится в пределах

поскольку сообщение при квантовании аппроксимируется с точностью до половины ступени квантования, равной 2/L. Мощность шума квантования равна дисперсии ε

При большом числе уровней квантования можно считать все значения е в пределах от  равновероятными. Тогда плотность вероятности p(ε) равна  , а дисперсия 

Учитывая, что мощность нормированного сигнала на выходе приемника равна  , найдем отношение мощности сигнала к мощности шума квантования

                                                                                           

Отсюда видно, что, выбрав достаточно большое число уровней квантования L (или большое число импульсов в комбинации k), можно получить сколь угодно высокое отношение сигнала к шуму квантования. Но большое число импульсов k можно обеспечить только при достаточно широком спектре сигнала. Действительно, частота следования кодовых комбинаций должна быть не менее чем 2Fm для одного канала или 2nFm в n-канальной системе. Следовательно, максимальная частота следования импульсов не может быть меньше 2knFm или длительность импульса   не может быть больше 1/2knFm.

Положим,  ,     где   — коэффициент, определяющий скважность импульсов. Для передачи радиоимпульса длительностью  , как известно, необходима полоса частот

где  - — коэффициент,  зависящий  от допустимого искажения формы импульса. Тогда

                                                                                                                      Определив отсюда k и подставив его значение, найдем

                                                                                                                      

Сравнивая эту формулу с, видим, что в системе ИКМ величина  , так же как и   в идеальной системе, экспоненциально растет с увеличением v. Система ИКМ приближалась бы к идеальной, если бы, помимо шумов квантования, никаких других помех на ее выходе не было. В действительности в системе ИКМ возникают и другие шумы, вызванные тем, что помехи в канале могут создавать ложные импульсы или подавлять импульсы сигнала.

В отличие от систем АИМ, ФИМ и ШИМ, где при приеме необходимо определять амплитуду, положение или длительность импульса, в системе ИКМ достаточно установить факт наличия или отсутствия импульса. Поэтому до тех пор, пока помехи на входе приемника лишь искажают амплитуду или смещают положение фронта импульса, они на выходной сигнал ИКМ не действуют. Только в тех случаях, когда интенсивность помехи на входе столь велика, что она вызывает ошибки в определении наличия или отсутствия импульса, к шумам квантования прибавляются дополнительные шумы.

Можно показать, что отношение сигнала к помехе в этом случае определяется следующим выражением:

                                                                                           

Приведенная формула справедлива для любого вида модуляции несущей. От вида модуляции зависит величина α², которая равна .

При больших значениях а можно применить асимптотическое разложение функции Ф(α) и преобразовать ф-лу к более простому виду. Действительно, так как

то при α>> 1

откуда при L>>l, p=2Fm и kП=

                                                                                                                                      

Порог помехоустойчивости в системе ИКМ-АМ, так же как и в импульсных системах модуляции, определяется порогом срабатывания приемника.

Наряду с системой ИКМ на практике находит применение другая цифровая система, которая называется системой дельта-модуляции (ДМ). В этой системе непрерывное сообщение также преобразуется в двоичный сигнал. При этом используется чрезвычайно простой способ декодирования. В системе ДМ передаваемый сигнал содержит импульсы положительной или отрицательной полярности (+1 или -1), а декодирующее устройство представляет собой простой интегрирующий контур, который суммирует все импульсы последовательности. На рисунке иллюстрируется преобразование непрерывного сообщения u(t) в ДМ сигнал. Полярность передаваемого импульса соответствует знаку производной сообщения u(t). Помехоустойчивость системы с ДМ определяется аналогичным с ИКМ методом.

Замечательным свойством систем с квантованием сигнала, в том числе систем ИКМ и ДМ, является возможность регенерации импульсов после того, как эти импульсы претерпели искажение при передаче по линии связи. Вследствие этого уменьшается влияние помех и значительно снижается накопление шумов при ретрансляции.