9. Привести общее выражение для разложения сигнала по ортонормированному базису и конкретизировать это выражение для случая непрерывных сигналов.

10. Привести общее выражение для разложения сигнала по ортонормированному базису и конкретизировать это выражение для случая дискретных сигналов.

Ответ:

Выражение для разложения сигнала по ортонормированному базису:

(1)

Или так (одно и то же):

- данное выражение является обобщенным рядом Фурье. (2)

Разложим произвольный сигнал s(t) в ряд:

1. Возьмем базисную функцию Uk с произвольным номером k, умножим на нее обе части равенства (2) и проинтегрируем во времени:

Этот базис можно использовать для НЕПРЕРЫВНЫХ сигналов с помощью системы гармонических функций:

Этот базис можно использовать для ДИСКРЕТНЫХ сигналов с помощью системы функций Уолша:

На отрезке своего существования [-T/2, T/2] принимают значения 1 и -1.

Введем безразмерное время и будем обозначать k-ю функцию Уолша как принято: wal(k, .

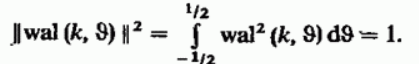
11. Привести равенство Парсеваля для случая непрерывных сигналов.

Ответ: Будем понимать под непрерывным сигналом любую, в общем случае комплекснозначную, функцию времени , на некотором вещественном интервале времени

Сигналы s, u называются ортогональными, если их скалярное произведение равно 0, т.е. : , 0. Система непрерывных сигналов, состоящая из конечного или бесконечного числа сигналов, называется ортогональной, если входящие в нее сигналы попарно ортогональны, т.е. , 0, , и ортонормированной, если кроме этого сигналы ei(t) имеют единичную энергию . Ортонормированная система н образует ортогональный базис, если любой сигнал н s может быть однозначно представлен в виде линейной комбинации базисных сигналов ek  Eн:

(7)

При этом справедливо классическое равенство Парсеваля

12. Привести равенство Парсеваля для случая дискретных сигналов.

Ответ: Под дискретным сигналом будем понимать любую, в общем случае комплекснозначную, последовательность на некотором целочисленном интервале времени Напоминание: символ означает «по определению равно»; – поле комплексных чисел; запись A B  означает, что A является подмножеством B или совпадает с B ; запись A B  – то же самое, но совпадение исключается. Часто дискретные сигналы получаются из непрерывных путем их равномерной дискретизации интервалом  R. В дальнейшем предполагается, что  ,  , а все рассматриваемые сигналы имеют конечную энергию, т.е.

( – модуль комплексного числа).

Совершенно аналогично определяются ортонормированный сигнальный базис, разложение по базису, размерность и др. в случае дискретного сигнального пространства д . В частности, формулы (7) и (8) принимают вид

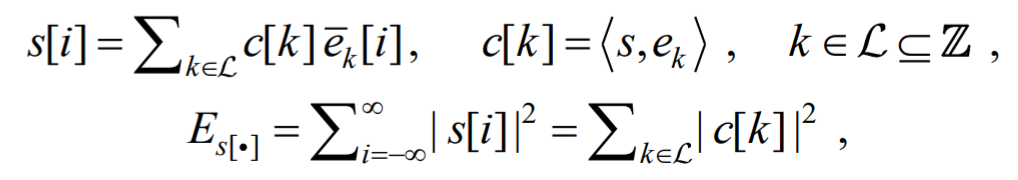(10)

где дискретный ортонормированный базис.

13. Дать определение пространства непрерывных частотно-ограниченных сигналов. Пространство непрерывных частотно-ограниченных сигналов: Ограниченность по частоте означает, что спектр сигнала отличен от нуля на некотором конечном интервале и равен нулю вне этого интервала. 14. Что называется базисом Котельникова и какие у него свойства? Определение базиса Котельникова:

Свойства базиса Котельникова: 1) Возможность восстановить функцию в любой точке, если была соблюдена теорема Котельникова, для этого нужно вычислить коэффициенты от известных значений функции (отсчетов) и найти их для последующих расчетов. 2) Работа в исключительном финитном спектре функции. Базис неприменим к функциям с бесконечным спектром.