23. Дать определение комплексной огибающей двухмерного qam сигнала и привести выражение для qam сигнала через его комплексную огибающую.

24. Привести классификацию ортогональных базисных сигналов, используемых в цифровых системах связи.

25. Понятия квадратурной, частотной и временной размерностей и как они связаны с общей размерностью сигнала.

n_Q 1, 2 (квадратурная размерность) – число квадратур, используемых при описании базисных функций Ф (t) l B ; n_t (временная размерность) – число различных базисных сигналов, ортогонально разнесенных по времени; f n (частотная размерность) – число различных базисных сигналов, ортогонально разнесенных по частоте. При этом n = n_Qn_tn_f. В частности, для PSK/QAM сигналов с временным разнесением n = n_Qn_t.

26. Записать базис для многомерного otdm сигнала. Понятие символьного интервала.

где i {1,…,M} . Такое объединение сигнальных компонент в англоязычной литературе называется мультиплексированием с ортогональным временным разделением (OTDM – Orthogonal Time Division Multiplexing), а получаемый в результате уплотненный сигнал (27) обозначается PSK-OTDM или QAM-OTDM, соответственно. В частном случае, n_t = 1 ансамбль (27) совпадает (18) или (22). Теоретически доказано [1,2], что при n_t  1 ортогональность сдвинутых по времени базисных сигналов Ф_q,p (t), p = 1,…,n_t возможна только когда формирующий импульс g(t) удовлетворяет критерию Найквиста (19). По этой причине OTDM технология иногда называется найквистовой передачей. Учитывая (16), (17), можно всегда однозначно восстановить 15 модулирующие символы и построить соответствующее многомерное PSK/QAM созвездие по формулам

где i_p {1,…,M}, i {1,…,M}. Точки такого созвездия имеют размерность n = n_Qn_t, их количество M совпадает с размером ансамбля (27). Локализация сигнала (27) на интервале [0, n_t, T ) означает, что значительная часть его энергии сосредоточена внутри данного интервала, но он не обязан быть финитным (равным нуля вне интервала). Отметим, что параметр T в сигналах OTDM (27) называется символьным интервалом и определяет минимальный временной сдвиг, при котором две соседние по времени базисные функции будут ортогональными.

Формулы:

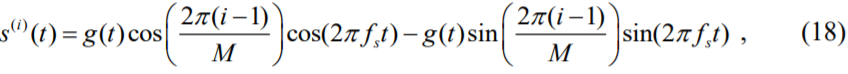
где i 1,…,M и g(t), t  R – четный формирующий импульс.

T – интервал корреляции импульса, M  2 – размер ансамбля, называемый индексом PSK модуляции; f_s  k / T , где k – натуральное число.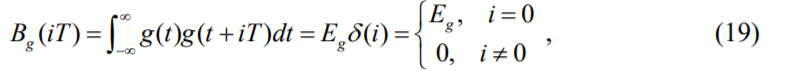

где i = (k-1) + l – номер сигнала.

27. Дать определение многомерного QAM-OTDM сигнала.

28. Записать выражение для сигнального созвездия OTDM сигнала.

29. Какому критерию должен удовлетворять формирующий импульс, входящий в описание OTDM сигнала и сформулировать этот критерий.

30. Привести графики корреляционных функций и спектральных плотностей семейства приподнятого косинуса для трех различных значений коэффициента ската.

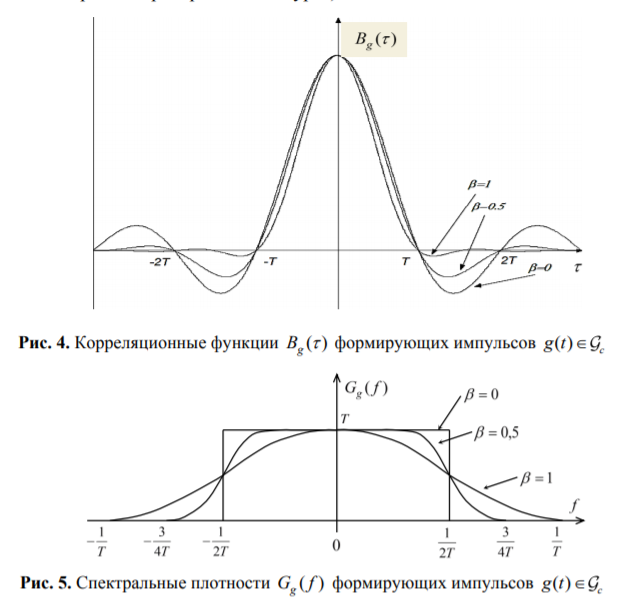
31. Нарисовать спектральные плотности OTDM сигнала и его низкочастотного формирующего импульса.

32. Записать модель аддитивного гауссовского канала и пояснить все входящие в нее элементы. Понятие непрерывной реализации.

Аддитивный гауссовский канал связи. Модулированный цифровым сообщением m(i) сигнал передается в канал связи, который случайным

33. Сформулировать задачу оптимального приема (постановка задачи, критерий максимума апостериорной вероятности).

34. Определить понятия статистики, выборки, достаточной статистики и минимальной достаточной статистики.

35. Привести общую структурную схему цифрового приемника и пояснить ее работу.

В случае цифровой реализации всех элементов приемника, сигнал r(t) дискретизируется и оцифровывается с помощью АЦП (изображена на схеме пунктиром), причем частота дискретизации должна обеспечивать качественное выполнение процедуры демодуляции. Демодуляцию сигнала можно выполнить и в аналоговой форме с использованием специализированных аналоговых микросхем. В этом случае оцифровка дискретной статистики выполняется на выходе демодулятора. Последующая процедура детектирования обычно всегда реализуется в цифровом виде.