Добавил:

Ivanoff228 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

Высшая математика

Файл:

Е. А. Ровба - Высшая математика

.pdf

Скачиваний:

180

Добавлен:

21.01.2022

Размер:

1.93 Mб

Скачать

☆

<<< < Предыдущая 17 18 19 20 21 22 23 24 25 26 27 28 2930 / 4130 31 32 33 34 35 36 37 38 39 40 41 > Следующая >>>

290 Глава 5. Теория интегрирования

наращиваемой суммы через 3 года ежегодные капиталовложения от 10 до 13 тыс. ден. ед. равносильны одновременным первоначальным вложениям 30,5 тыс. ден. ед. при той же начисляемой непрерывно процентной ставке.

5.5. Несобственные интегралы

5.5.1.Обобщение понятия определенного интеграла

Определенный интеграл f(x) dx рассматривался при двух

условиях:

1)промежуток [a, b] конечен,

2)функция f ограничена на отрезке [a, b].

Если хотя бы одно из этих условий не выполняется, то данное в

§ 5.3 определение интеграла f(x) dx не имеет смысла. Если, напри-

мер, промежуток интегрирования бесконечный, то его нельзя разбить на n частей конечной длины. Если же функция f не ограничена на отрезке [a, b], то не существует конечного предела интегральных сумм. Обобщим понятие интеграла и на эти случаи.

5.5.2.Несобственный интеграл с бесконечными пределами интегрирования

Предположим, что функция задана на промежутке [a, +∞) и является интегрируемой на любом конечном отрезке [a, A], a < A, т.е. существует интеграл

f(x) dx.

5.5. Несобственные интегралы	291

Определение 5.8. Несобственным интегралом первого рода или несобственным интегралом с бесконечным пределом интегрирования

	+∞
	*a	f(x) dx
называется предел
			A
	lim		f(x) dx,		(5.43)
	A→∞	*a
т.е.
+∞				A
*a			lim	f(x) dx.
*a	f(x) dx =		A→∞	*a

Определение 5.9. Если предел (5.43) существует и конечен, то говорят, что несобственный интеграл сходится; если же этот предел не существует или бесконечен, то интеграл

*+∞

f(x) dx

называется расходящимся.

Рассмотрим геометрическую интерпретацию несобственного интеграла первого рода. Пусть, например, функция f является неотрицательной и невозрастающей на промежутке [a, +∞) (рис. 5.13).

y
	y = f(x)
O a	A	x
	Рис. 5.13

Интеграл f(x) dx численно равен площади заштрихованной

криволинейной трапеции. При возрастании A эта площадь будет

292	Глава 5. Теория интегрирования

увеличиваться. При этом она может неограниченно возрастать либо оставаться ограниченной и стремиться к какому-то пределу. Этот

предел и есть

*+∞

f(x) dx.

Подчеркнем, что площадь фигуры, заключенной между графиком функции y = f(x) и осью Ox вправо от точки x = a, может быть конечной, несмотря на то что эта фигура является неограниченной.

Геометрический смысл несобственного интеграла первого рода

состоит в том, что он численно равен площади полубесконечной фигуры, ограниченной графиком неотрицательной функции, прямой x = a и отрезком [a, +∞] оси Ox.

	+∞
Пример 5.33. Вычислить несобственный интеграл	*0	e−x dx

(или установить его расходимость).

Р е ш е н и е. По определению (см. выражение (5.43)) имеем:

+∞

−e

−A

e−x dx =

lim

e−x dx =

lim

−x

A→+∞

lim (1

−

) = 1.

A→+∞

+∞

Пример 5.34. Вычислить несобственный интеграл

(или

установить его расходимость).

Р е ш е н и е. Находим:

+∞	dx =	A	dx = lim		A
					A
1		1					lim	ln A = + .
		lim					lim	ln A = + .
*	x	A→+∞ *	x A→+∞	ln x 1		=	A→+∞	∞

Следовательно, этот интеграл расходится.

5.5. Несобственные интегралы

293

Замечание 5.5. Несобственный интеграл

+∞

= 1,

xα

сходится при α > 1 и расходится при α 1.

Д о к а з а т е л ь с т в о. По определению

+∞

dx lim x−α dx =

lim

x1−α

A→+∞

xα

= A→+∞ *

−

1−α

− 1), α = 1.

= 1

lim

−

A→+∞(A

Предположим, что 1 − α < 0, т.е. α > 1. Тогда имеем:

+∞

lim (A1−α

−

1) =

−

−1

A→+∞

xα

1 − α

+∞

т.е. несобственный интеграл

сходится при α > 1 и его значение

xα

равно (α − 1)−1.

Пусть теперь 1 − α > 0, т.е. α < 1. Тогда

lim

(A1−α

−

1) = +

∞

A→+∞

и интеграл расходится. Учитывая пример 5.34, заключаем, что инте-

	+∞
грал	*1	dx	расходится при α 1.
		xα

Замечание 5.5 свидетельствует о том, что функция f(x) = 1/xα в случае α > 1 достаточно быстро стремится к нулю при x → +∞, и

+∞

	*	dx
это обеспечивает существование несобственного интеграла			.
		xα

294	Глава 5. Теория интегрирования

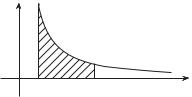
Если же α 1, то f(x) = 1/xα стремится к нулю медленно при x → +∞ или совсем не стремится к нулю, и поэтому рассматриваемый интеграл расходится.

Аналогично вводится понятие несобственного интеграла по промежутку (−∞, b]:

*	B*
b	b
f(x) dx = lim	f(x) dx.
b→−∞
−∞

Предположим, что функция f определена на всей числовой прямой (−∞, +∞). Теперь рассмотрим интеграл

+∞
* f(x) dx.	(5.44)

−∞

Фиксируем произвольное число c R. Разобьем интеграл (5.44) на два интеграла:

*	*	*c
+∞	c	+∞
f(x) dx =	f(x) dx +	f(x) dx,	(5.45)
−∞	−∞

где c — произвольное число.

Интеграл (5.44) называют сходящимся, если оба интеграла в правой части равенства (5.45) сходятся, и расходящимся — в противном случае.

5.5.3. Интегралы от неограниченных функций

Предположим, что функция f не ограничена на отрезке [a, b]. Обобщим понятие интеграла на этот случай.

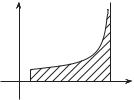
Пусть функция f определена на промежутке [a, b). В любой окрестности точки x = b функция f может быть неограниченной. Предположим, что функция f интегрируема на любом отрезке [a, b1] [a, b), т.е. существует интеграл

*b1

f(x) dx, b1 [a, b).

5.5. Несобственные интегралы						295

Определение 5.10. Несобственным интегралом второго рода
от функции f(x) на отрезке [a, b] называется предел
			b1	f(x) dx,		(5.46)
b1	→b−0		*a	f(x) dx,		(5.46)
	lim
т.е.					b1
b					b1
f(x) dx			lim		f(x) dx.
*a		= b1→b−0			*a

Если предел (5.46) существует и конечен, то рассматриваемый интеграл называется сходящимся, в противном случае — расходящимся.

Геометрический смысл несобственного интеграла второго рода

состоит в том, что данный интеграл численно равен площади полубесконечной фигуры, ограниченной графиком неотрицательной функции, прямыми x = a, x = b и частью оси Ox (рис. 5.14).

y
		y = f(x)
O	a	b	x
		Рис. 5.14

Если функция f определена на промежутке (a, b] и не ограничена в окрестности точки x = a, то полагают, что

b	b
*a	lim	f(x) dx.
*a	f(x) dx = a1→a+0a*1
Наконец, пусть	функция f определена на интервале (a, b) и

не ограничена и в окрестности точки a, и в окрестности точки b. Произвольным образом выберем число c (a, b). Получим:

*b f(x) dx = *c f(x) dx + *b f(x) dx.

(5.47)

296	Глава 5. Теория интегрирования

Несобственный интеграл

f(x) dx

называют сходящимся, если оба интеграла в правой части равенства (5.47) сходятся, и расходящимся — в противном случае.

Пример 5.35. Вычислить несобственный интеграл

√ dx

1 − x2

(или установить его расходимость).

Р е ш е н и е. Данный интеграл является несобственным интегра-

√

лом второго рода. Функция f(x) = 1/ 1 − x2 не ограничена в любой окрестности точки x = 1, поэтому по формуле (5.46) имеем:

1		−
0		−
*		dx						π
				lim	arcsin x b1	= lim			.
	√1		x2 = b1→1−0		0	b1→1−0 arcsin b1	= arcsin 1 =	2

Пример 5.36. Вычислить несобственный интеграл

*1 dx

(или установить его расходимость).

Р е ш е н и е. По определению несобственного интеграла второго рода имеем:

1	1		dx =	lim	1	lim (ln 1	ln a ) = .
	dx = lim
*		a1→+0 *
	x		x	a1→+0 ln \|x\| a1		= a1→+0	− 1 ∞

0a1

Значит, указанный интеграл расходится.

5.5. Несобственные интегралы	297

Замечание 5.6. Несобственный интеграл

xα , α R,

сходится при α < 1 и расходится при α 1.

Д о к а з а т е л ь с т в о. В этом интеграле функция f(x) = 1/xα может быть неограниченной в окрестности точки x = 0.

По определению имеем:

1			1
*	dx	lim	*	dx	.
	xα
		= a1→+0		xα

0a1

Случай α = 1 рассмотрен в примере

5.36. Этот

интеграл

расходится.

Если α = 1, то

1−α

x−α dx =

a 1−α).

lim (1

lim

−

xα = a1→+0

a1→+0

−

α a1→+0

Рассмотрим два случая: α < 1 и α

> 1. Если α < 1, то

lim

−

a 1−α) = 1,

a1→+0

xα

1 − α

Если же α > 1, то

lim

1−α) =

lim

a1→+0(1 − a1

a1→+0 1 − a1α−1 = −∞.

Следовательно, интеграл

*1 dx

xα

сходится, если α < 1, и расходится, если α 1.

Мы рассмотрели понятие несобственных интегралов. В расширенном курсе высшей математики подробно рассматриваются условия их сходимости и устанавливаются соответствующие признаки.

Глава 6

Дифференцирование функций двух переменных

6.1.Функция двух переменных. Дифференциал

6.1.1. Определения

Понятие функции двух переменных вводится во многом аналогично понятию функции одной переменной. В этой главе мы рассматриваем функции двух переменных, однако все сказанное здесь нетрудно переносится и на функции n переменных.

Определение 6.1. Обозначим через D некоторое множество точек M(x, y) плоскости R2. Правило f, ставящее в соответствие каждой упорядоченной паре действительных чисел (x, y) D единственное число z из множества действительных чисел R, называется функцией двух переменных и обозначается z = f(x, y), z = f(M) либо f : D → R. Множество D при этом называется областью определения функции.

Множество

	f(x, y) (x, y) D

называется множеством значений функции f.

Множество значений является подмножеством множества действительных чисел R, а область определения — подмножеством точек плоскости Oxy.

6.1. Функция двух переменных. Дифференциал	299

Функцию двух переменных можно изобразить графически. Для этого в каждой точке (x, y) D вычисляется значение функции

z = f(x, y). Тогда тройка чисел (x, y, z)			= (x, y, f(x, y)) определяет
в системе декартовых координат в пространстве некоторую точку P
(рис. 6.1).
	z
	z
	f(x, y)
			z = f(x, y)
		P
	O		y
	O
			y
x		M
		M
x
		Рис. 6.1
Определение 6.2. Совокупность			всех точек P (x, y, f(x, y)),

(x, y) D (рис. 6.1), представляет собой поверхность в трехмерном пространстве, которая называется графиком функции z = f(x, y).

Пример 6.1. Графиком линейной функции z = Ax + By + C является плоскость.

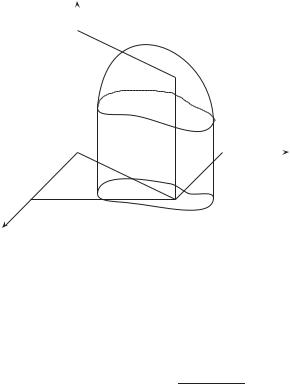
Пример 6.2. Для функции z = 1 − x2 − y2 область определения D(f) есть единичный круг x2 + y2 1, а множество значений — отрезок [0, 1]. График этой функции представляет собой поверхность, похожую на верхнюю полусферу единичного радиуса с центром в начале координат (рис. 6.2).

Наглядное представление о функции двух или трех переменных может дать картина ее линий уровня.

<<< < Предыдущая 17 18 19 20 21 22 23 24 25 26 27 28 2930 / 4130 31 32 33 34 35 36 37 38 39 40 41 > Следующая >>>