9. Феррорезонанс в цепи с последовательным соединением нелинейной индуктивности и емкости

Рассмотрим электрическую цепь, состоящую из последовательно соединенных элементов: резистора, катушки с ферромагнитным сердечником и конденсатора.

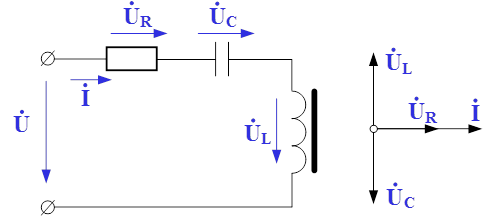
Рис.1. Схема замещения электрической цепи для исследования феррорезонанса напряжений

По второму закону Кирхгофа для представленного колебательного контура можно записать следующее выражение:

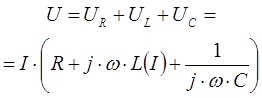
Следует обратить внимание на то, что индуктивность в ферромагнитном элементе меняется в зависимости от величины тока в сети, поэтому она показа функцией от тока -  .

В связи с наличием в расчетной схеме нелинейного элемента, анализ работы данной схемы будем выполнить графоаналитическим способом, с помощью которого получим зависимость изменения напряжения от тока в расчетной схеме сети. Так же следует заметить, чтобы возникло явление феррорезонанса в расчетной схеме (для основной гармоники) необходимо, чтобы вольт-амперные характеристики катушки с ферромагнитным сердечником и конденсатора пересекались.

Вначале рассмотрим характеристику изменения напряжения от тока в расчётной схеме в идеализированном случае: для этого сделаем допущение об отсутствии активных потерь в колебательном контуре. Напряжение на емкости   изменяется  пропорционально изменению тока, тогда как напряжение на катушке индуктивности   изменяется по нелинейной характеристике. Напряжение на емкости и катушке индуктивности сдвинуты по фазе на угол 180 градусов, но для удобства на графике изображены по одну сторону оси. Точка пересечения графиков    и   соответствует феррорезонансу напряжений.

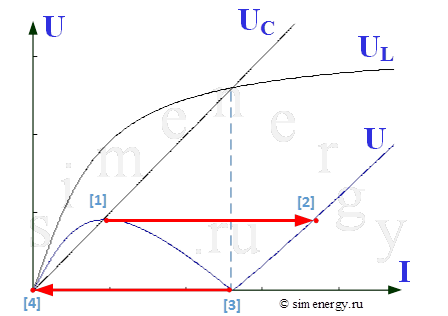
Рис.2. Зависимость напряжения от тока при отсутствии активного сопротивления (вольт-амперная характеристика)

Из полученной характеристики видно, что при постепенном увеличении питающего напряжения (U) до точки [1] величина тока плавно растет (ток по фазе отстает от напряжения, в том числе UL>UC).  В точке [1] при незначительном увеличении напряжения происходит скачок тока, при котором ток резко возрастает до значения, соответствующего точке [2].

При снижении напряжения U до точки [3] величина тока плавно уменьшается, а затем скачком снижается от точки [3] до точки [4].

Явление резкого изменения тока в цепи при незначительном изменении напряжения на входе называется триггерным эффектом в последовательной феррорезонансной цепи.

В случае наличия активного сопротивления в расчетной схеме (например, при учете активных потерь в стали и в сопротивлении обмотки), зависимость  U(I) приобретает вид, приведенный на рис 3. Данная кривая также имеет несколько участков.

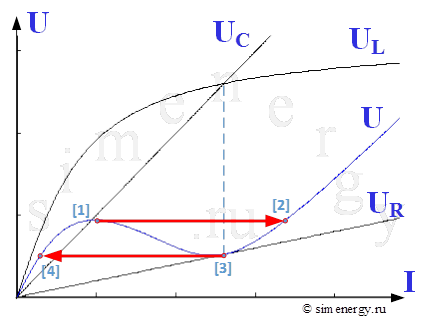
Рис.3. Зависимость напряжения от тока при наличии активного сопротивления (вольт-амперная характеристика)

В заключении следует отметить, что феррорезонанс напряжений в расчетной схеме можно достичь путем изменения напряжения или частоты источника питания схемы, а также путем изменения емкости и параметров катушки со стальным сердечником. 

9. Феррорезонанс в цепи с параллельным соединением нелинейной индуктивности и емкости

Рассмотрим электрическую цепь, состоящую из параллельно соединенных элементов: резистора, катушки с ферромагнитным сердечником и конденсатора.

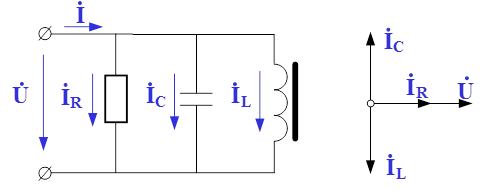
Рис.4. Схема замещения электрической цепи для исследования феррорезонанса токов

По первому закону Кирхгофа для представленного колебательного контура можно записать следующее выражение:

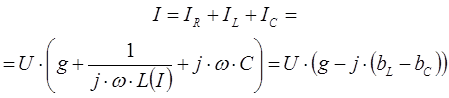
Следует обратить внимание на то, что индуктивность в ферромагнитном элементе меняется в зависимости от величины тока в сети, поэтому она показа функцией от тока -  .

В связи с наличием в расчетной схеме нелинейного элемента, анализ работы данной схемы будем выполнить графоаналитическим способом, с помощью которого получим зависимость изменения напряжения от тока в расчетной схеме сети. Так же следует заметить, чтобы можно было достичь феррорезонанса для основной гармоники тока катушки и конденсатора, необходимо, чтобы вольт-амперные характеристики катушки с ферромагнитным сердечником и конденсатора пересекались.

Вначале рассмотрим характеристику изменения напряжения от тока в расчётной схеме в идеализированном случае: для этого сделаем допущение об отсутствии активных потерь в колебательном контуре. Ток, протекающий через емкость,   изменяется  пропорционально изменению напряжения, тогда как ток, протекающий через катушку индуктивности  , изменяется по нелинейной характеристике. Ток, протекающий через емкость, и ток, протекающий через катушку индуктивности, сдвинуты по фазе на угол 180 градусов, но для удобства на графике изображены по одну сторону оси. Точка пересечения графиков    и   соответствует феррорезонансу токов.

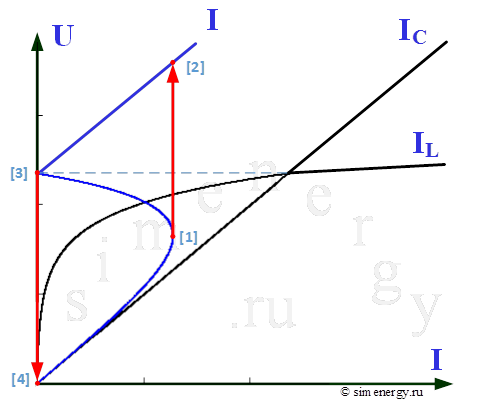
Рис.5. Зависимость напряжения от тока при отсутствии активного сопротивления (вольт-амперная характеристика)

Из полученной характеристики видно, что при постепенном увеличении тока I величина напряжения  сначала плавно растет (ток по фазе отстает от напряжения, в том числе UL>UC).  В точке [1] при незначительном увеличении тока происходит скачок напряжения, при котором напряжение резко возрастает до значения, соответствующего точке [2]. Дальнейшее возрастание тока сопровождается плавным увеличением значения напряжения.

При снижении тока I  до точки [3] величина напряжения плавно уменьшается, а затем скачком снижается от точки [3] до точки [4].

Явление резкого изменения напряжения в цепи при незначительном изменении тока источника питания, сопровождающиеся изменением знака угла сдвига фаз между основными гармониками тока и напряжения в цепи,  называется триггерным эффектом в последовательной феррорезонансной цепи.

В случае наличия активного сопротивления в расчетной схеме (например, при учете активных потерь в стали и в сопротивлении обмотки), зависимость  U(I) приобретает вид, приведенный на рис 6. Данная кривая также имеет несколько участков.

Рис.6. Зависимость напряжения от тока при наличии активного сопротивления (вольт-амперная характеристика)

В заключении следует отметить, что феррорезонанс токов в расчетной схеме можно достичь путем изменения тока или частоты источника питания схемы, а также путем изменения емкости и параметров катушки со стальным сердечником. Аналогичные феррорезонансные явления могут наблюдаться в случае линейной индуктивности и нелинейной емкости или нелинейных индуктивности и емкости.