
- •Основные свойства нелинейных элементов в электрических цепях постоянного тока
- •Графические методы расчета нелинейных цепей постоянного тока
- •Расчет нелинейных магнитных цепей постоянного тока: прямая задача
- •Регулярные методы расчета
- •1. Прямая” задача для неразветвленной магнитной цепи
- •2. “Прямая” задача для разветвленной магнитной цепи
- •Графические методы расчета
- •Расчет нелинейных магнитных цепей постоянного тока: обратная задача
- •1. “Обратная” задача для неразветвленной магнитной цепи
- •2. “Обратная” задача для разветвленной магнитной цепи
- •8. Особенности поведения безинерционных элементов в электрических цепях при периодических процессах
- •Особенности поведения инерционных элементов в электрических цепях при периодических процессах
- •Метод эквивалентных синусоид
- •Метод кусочно-линейной аппроксимации
- •Потери в ферромагнитных сердечниках при периодическом изменении магнитного потока
- •Уравнение, векторная диаграмма и схема замещения катушки с ферромагнитным сердечником
- •Феррорезонанс в цепи с последовательным соединением нелинейной индуктивности и емкости
- •Феррорезонанс в цепи с параллельным соединением нелинейной индуктивности и емкости
- •Устойчивость режимов работы нелинейной электрической цепи
- •Расчет цепей с полупроводниковыми приборами
- •Основные положения теории электромагнитного поля
- •Система уравнений электромагнитного поля в интегральной форме
- •Система уравнений электромагнитного поля в дифференциальной форме
- •Граничные условия на поверхности раздела двух сред
- •Электростатическое поле и его свойства
- •Потенциал - энергетическая характеристика электрического поля.
- •Граничные условия в электростатическом поле
- •Метод зеркальных изображений
- •Потенциал, градиент потенциала. Уравнение Пуассона и Лапласа
- •Электрическое поле постоянного тока
- •Электростатическая аналогия
- •Магнитное поле постоянного тока. Векторный и скалярный магнитный потенциал
- •Переменное электромагнитное поле в диэлектрике
- •Плоская электромагнитная волна в диэлектрической однородной и изотропной среде
- •Вектор Пойнтинга. Энергия электромагнитного поля
- •Теорема Умова-Пойнтинга
- •Переменное электромагнитное поле в проводящей среде
- •Электрический и магнитный поверхностный эффект
- •Эффект близости
- •Электромагнитное экранирование
Потери в ферромагнитных сердечниках при периодическом изменении магнитного потока
|
Эти
потери складываются из потерь на вихревые
токи и на гистерезис. Сердечники набирают
из тонких листов железа, покрытых лаком
(рис. 11.3). Лак служит изоляцией, поэтому
потери на вихревые токи уменьшаются.
Ток ie,
протекающий по катушке, намотанной на
сердечник, создает магнитное поле ![]() ,
которое проходит по сердечнику вдоль
листов.
,
которое проходит по сердечнику вдоль
листов.
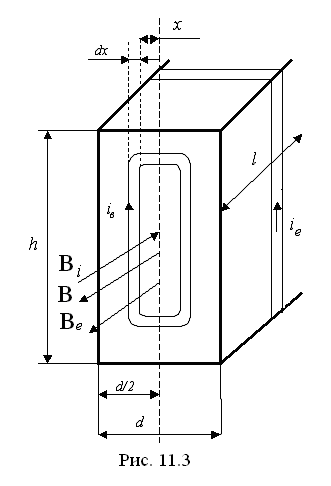
Это
поле индуцирует в сердечнике вихревой
ток. Поперечное сечение этой трубки
вихревого тока равно ldx,
длина трубки ~ 2h.
Поле вихревого тока ![]() направленно
против поля катушки
.
Т.о., в сердечнике действует результирующее
поле с индукцией
направленно
против поля катушки
.
Т.о., в сердечнике действует результирующее
поле с индукцией ![]() .
Это результирующее поле распределено
неравномерно по полю сердечника, т.к.
вихревое поле имеет наибольшее значение
вдоль оси сердечника. Здесь мы будем
пренебрегать этой неравномерностью и
полагать, что
всюду
по сечению одно и то же.
.
Это результирующее поле распределено
неравномерно по полю сердечника, т.к.
вихревое поле имеет наибольшее значение
вдоль оси сердечника. Здесь мы будем
пренебрегать этой неравномерностью и
полагать, что
всюду
по сечению одно и то же.
Рассчитаем ЭДС, индуцируемой вдоль трубки:
![]() ,
,
обозначим ![]() ,
тогда
,
тогда 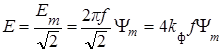 ,
где
,
где ![]() -
коэффициент формы кривой ЭДС.
-
коэффициент формы кривой ЭДС.
Действующее значение ЭДС, индуцируемой вдоль трубки, равно:
![]() ,
,
Коэффициент формы поля:
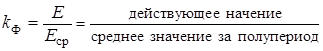 .
.
В
случае синусоиды ![]() ;
; ![]() ,
, ![]() ,
тогда действующее значение равно
,
тогда действующее значение равно
![]() .
.
Потери
внутри трубки тока равны: ![]() ,
где
,
где ![]() -
проводимость трубки.
-
проводимость трубки.
![]() .
.
Проинтегрируем полученное выражение.
![]() ,
(11.1)
,
(11.1)
где V=hld – объем сердечника.
Таким образом, потери на вихревые токи при условии =const пропорциональны квадрату частоты, квадрату амплитуды магнитной индукции, квадрату толщины сердечника и первой степени удельной проводимости. Если сердечник набран из проволок круглого сечения с диаметром d, оси которых направлены вдоль магнитного поля, то в формуле (11.1), вместо 4/3, имеем коэффициент 1/2. Поэтому в общем виде можно записать:
![]() .
.
 Было
показано, что ферромагнитный сердечник,
находящийся в периодическом изменяющемся
во времени внешнем магнитном поле,
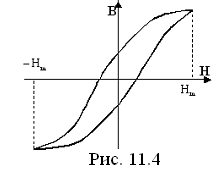
перемагничивается. Это перемагничивание
происходит по гистерезисной петле (рис.
11.4), причем, каждой петле соответствует
один период изменения внешнего магнитного
поля. Поскольку перемагничивание связано
с поворотом элементарных токов (магнитов)
тела под действием внешнего магнитного
поля, то источнику внешнего магнитного
поля приходится совершать работу. Эта
работа выделяется в теле в виде потерь,
называемых потерями на гистерезис. Эти
потери в единице
объема тела за один
цикл перемагничивания
оказываются равными площади гистерезисной
петли.
Было
показано, что ферромагнитный сердечник,
находящийся в периодическом изменяющемся
во времени внешнем магнитном поле,
перемагничивается. Это перемагничивание
происходит по гистерезисной петле (рис.
11.4), причем, каждой петле соответствует
один период изменения внешнего магнитного
поля. Поскольку перемагничивание связано
с поворотом элементарных токов (магнитов)
тела под действием внешнего магнитного
поля, то источнику внешнего магнитного
поля приходится совершать работу. Эта
работа выделяется в теле в виде потерь,
называемых потерями на гистерезис. Эти
потери в единице
объема тела за один
цикл перемагничивания
оказываются равными площади гистерезисной
петли.
![]() .
.
Штейнмец предложил экспериментальную формулу вида:
![]() ,
,
где ![]() -
амплитуда магнитной индукции,
-
амплитуда магнитной индукции, ![]() -
коэффициент, зависящий от рода материала.
-
коэффициент, зависящий от рода материала.
Формула
Штейнмеца дает удовлетворительное
согласие с экспериментом при ![]() .
При
.
При ![]() ,
а также при
,
а также при ![]() лучшее
приближение дает формула:
лучшее
приближение дает формула:
![]() .
.
Обе формулы можем объединить в одну:
![]() .
(11.2)
.
(11.2)
При
большой частоте изменения напряженности
магнитного поля вид петли B=f(H)
отличается от статической петли
гистерезиса, получаемой при медленных
изменениях напряженности магнитного
поля, т.к. при этом магнитная индукция
является функцией не только Н,
но и ![]() .
Причиной этого являются вихревые токи
и магнитная вязкость. Площадь динамической
петли, выражающей B=f(H),
определяет полные потери в единице
объема вещества на перемагничивание и
на вихревые токи за один
период изменения
напряженности магнитного поля.
.
Причиной этого являются вихревые токи
и магнитная вязкость. Площадь динамической
петли, выражающей B=f(H),
определяет полные потери в единице
объема вещества на перемагничивание и
на вихревые токи за один
период изменения
напряженности магнитного поля.
При промышленной частоте (50 Гц) потери на гистерезисе можно вычислить независимо от потерь на вихревые токи на основе формулы (11.2)
![]() .
.
Таким образом, суммарная мощность потерь в сердечнике определяется по формуле:
![]() .
.
Определив
(например, экспериментально) ![]() при
двух различных частотах (f1, f2)
и одном значении магнитной индукции
,
можно разделить
при
двух различных частотах (f1, f2)
и одном значении магнитной индукции
,
можно разделить ![]() и
и ![]() .
.
![]() ,
(11.3)
,
(11.3)
![]() .
(11.4)
.
(11.4)
Умножим
уравнение (11.3) на ![]() ,
а уравнение (11.4) на -
,
а уравнение (11.4) на - ![]() ,
и найдем их разность (
,
и найдем их разность ( ![]() ):
):
![]() ,
,
Получили формулу для потерь на вихревые токи:
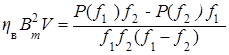 .
.
Затем
умножим уравнение (11.3) на ![]() ,
а уравнение (11.4) на -
,
а уравнение (11.4) на - ![]() ,
и найдем их разность (
,
и найдем их разность ( ![]() ):
):
![]() ,
,
Получили формулу для потерь на гистерезис:
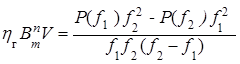 .
.
