
- •Основные свойства нелинейных элементов в электрических цепях постоянного тока
- •Графические методы расчета нелинейных цепей постоянного тока
- •Расчет нелинейных магнитных цепей постоянного тока: прямая задача
- •Регулярные методы расчета
- •1. Прямая” задача для неразветвленной магнитной цепи
- •2. “Прямая” задача для разветвленной магнитной цепи
- •Графические методы расчета
- •Расчет нелинейных магнитных цепей постоянного тока: обратная задача
- •1. “Обратная” задача для неразветвленной магнитной цепи
- •2. “Обратная” задача для разветвленной магнитной цепи
- •8. Особенности поведения безинерционных элементов в электрических цепях при периодических процессах
- •Особенности поведения инерционных элементов в электрических цепях при периодических процессах
- •Метод эквивалентных синусоид
- •Метод кусочно-линейной аппроксимации
- •Потери в ферромагнитных сердечниках при периодическом изменении магнитного потока
- •Уравнение, векторная диаграмма и схема замещения катушки с ферромагнитным сердечником
- •Феррорезонанс в цепи с последовательным соединением нелинейной индуктивности и емкости
- •Феррорезонанс в цепи с параллельным соединением нелинейной индуктивности и емкости
- •Устойчивость режимов работы нелинейной электрической цепи
- •Расчет цепей с полупроводниковыми приборами
- •Основные положения теории электромагнитного поля
- •Система уравнений электромагнитного поля в интегральной форме
- •Система уравнений электромагнитного поля в дифференциальной форме
- •Граничные условия на поверхности раздела двух сред
- •Электростатическое поле и его свойства
- •Потенциал - энергетическая характеристика электрического поля.
- •Граничные условия в электростатическом поле
- •Метод зеркальных изображений
- •Потенциал, градиент потенциала. Уравнение Пуассона и Лапласа
- •Электрическое поле постоянного тока
- •Электростатическая аналогия
- •Магнитное поле постоянного тока. Векторный и скалярный магнитный потенциал
- •Переменное электромагнитное поле в диэлектрике
- •Плоская электромагнитная волна в диэлектрической однородной и изотропной среде
- •Вектор Пойнтинга. Энергия электромагнитного поля
- •Теорема Умова-Пойнтинга
- •Переменное электромагнитное поле в проводящей среде
- •Электрический и магнитный поверхностный эффект
- •Эффект близости
- •Электромагнитное экранирование
Особенности поведения инерционных элементов в электрических цепях при периодических процессах
При наличии в цепи только инерционных элементов обеспечивается постоянство параметров этих элементов в течение периода изменения токов и напряжений. При синусоидальном воздействии токи и напряжения ветвей в этом случае будут синусоидальны и для расчета таких цепей возможно применение символического метода.
Однако при изменении установившегося режима, например, вследствие изменения действующего значения приложенного напряжения изменяются параметры нелинейных элементов за счет изменения действующих значений токов. В результате происходит перераспределение токов ветвей в другой пропорции, чем изменение приложенного напряжения, изменяются комплексные сопротивления ветвей цепи:
![]() .
(43)
.
(43)
Так
как модули ![]() и
аргументы
и
аргументы ![]() этих
сопротивлений являются функциями
действующих значений протекающих по
ним токов.
этих
сопротивлений являются функциями
действующих значений протекающих по
ним токов.
Для цепей с инерционными нелинейными элементами применяются графические методы расчета, рассмотренные ранее. Покажем их применение на конкретном примере.
 Пример
7. Требуется
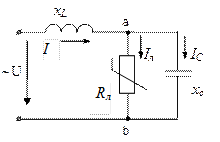
определить токи в ветвях схемы на рис.30.
Конденсатор и индуктивность линейны и
имеют сопротивления
Пример
7. Требуется
определить токи в ветвях схемы на рис.30.
Конденсатор и индуктивность линейны и
имеют сопротивления ![]() =50
Ом;
=50
Ом; ![]() =20
Ом. ВАХ инерционного нелинейного
сопротивления (лампа накаливания) задана
уравнением:
=20
Ом. ВАХ инерционного нелинейного
сопротивления (лампа накаливания) задана
уравнением:
![]()
Действующее
значение входного напряжения задано ![]() =300
В.
=300
В.
Рис.30. Схема цепи
Решение. Расчет и построение ВАХ всей цепи целесообразно вести в следующей последовательности:
 1.
Задаемся током лампы:
1.
Задаемся током лампы: ![]() .
(
.
( ![]() принимаем
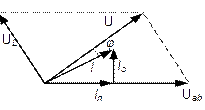
равной нулю). Векторная диаграмма токов
и напряжений цепи представлена на
рис.31. Находим комплекс напряжения на
участке ab:
принимаем
равной нулю). Векторная диаграмма токов
и напряжений цепи представлена на
рис.31. Находим комплекс напряжения на
участке ab:
![]() .
.
2. Определяем комплекс тока конденсатора
![]() .
.
Рис.31. Векторная диаграмма
3. Находим комплекс общего тока:
![]() .
.
4. Определяем входное напряжение
![]() ,
,
![]() .
.
5. Находим входное сопротивление:
![]()
Задаваясь
значениями тока ![]() ,
по описанному выше алгоритму рассчитаем
токи ветвей, напряжения и сопротивление
всей цепи.
,
по описанному выше алгоритму рассчитаем
токи ветвей, напряжения и сопротивление
всей цепи.
Для =1 А, получим:
=10·1+4·12=14 В;
![]() А;
А;
![]() А;
А;
![]() В;
В;
![]() В;
В;
![]() Ом.
Ом.
Результаты расчетов сводим в таблицу 9.
Результаты расчетов: действующие значения Таблица 9
|
|
|
|
|
|
|
|
|
0,28 |
1,038 |
20,77 |
21,7 |
20,88 |
|
|
0,72 |
2,12 |
42,5 |
45,45 |
21,38 |
|
|
1,32 |
3,27 |
65,55 |
71,9 |
21,9 |
|
|
2,08 |
4,5 |
90,1 |
101,45 |
22,5 |
|
|
4,08 |
7,25 |
145,1 |
171,4 |
23,6 |
|
|
6,72 |
10,44 |
208,9 |
257,3 |
24,6 |
8,85 |
401,8 |
8,03 |
11,95 |
|
299,07 |
25,01 |
8,87 |
403,4 |
8,068 |
12,1 |
239,8 |
300,1 |
25,02 |
8,875 |
403,8 |
8,07 |
|
|
300,3 |
25,03 |
8,95 |
405,8 |
8,11 |
12,04 |
240,9 |
301,62 |
25,04 |
|
|
8,28 |
12,22 |
244,8 |
306,76 |
25,08 |
|
|
|
14,1 |
282,5 |
360,5 |
25,49 |
|
|
13,92 |
18,4 |
367,5 |
481,6 |
26,2 |
|
|
18,48 |
23,1 |
463,6 |
621,1 |
26,78 |
По
результатам расчета построим
зависимости ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
(рис. 32).
,
(рис. 32).
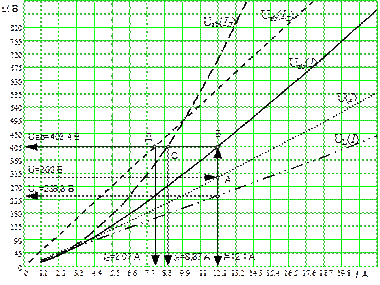
Рис.32. Графическое определение токов ветвей
Графически
определяем токи и напряжения:
=12,1
А;
=8,87
А; ![]() =8,07
А;
=8,07
А; ![]() =403,4
В;
=239,8
В.
=403,4
В;
=239,8
В.
