9. Электрический и магнитный поверхностный эффект

Переменный электрический ток (в том числе и синусоидальный) в отличие от постоянного неравномерно распределяется по сечению токопровода. При этом всегда существует тенденция вытеснения тока из внутренней части проводника в периферийную. Это явление называютэлектрическим поверхностным эффектом.

Если частота тока и параметры таковы, что глубина проникновения волны много меньше поперечного сечения проводника ( ), то ток в проводнике будет сосредоточен лишь в тонком поверхностном слое, толщина которого практически определяется глубиной проникновения волны. Такой поверхностный эффект называютярко выраженным. Вытеснение тока приводит к увеличению активного сопротивления токопровода по сравнению с его значением при постоянном токе. Если глубина проникновения волны соизмерима с габаритными размерами, то проводник называютпрозрачным и считают, что по сечению этого проводника ток распределяется практически равномерно.

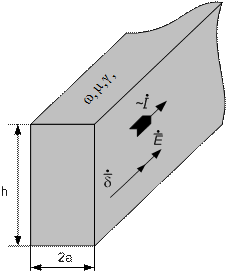
На рис. 30 изображена шина прямоугольного сечения, обтекаемая током I. Поле в шине удовлетворяет уравнению Гельмгольца

 

 

 

Электрический поверхностный эффект на примере шины прямоугольного сечения. Внутри шины существуют электромагнитное поле и ток проводимости. За пределами шины (удельная проводимость γ=0) ток проводимости (δ=0) отсутствует, но электрическое и магнитное поля существуют.

Рассчитаем распределение поля  и  в объеме прямоугольной шины (рис. 31) и вычислим ее комплексное сопротивление синусоидальному току, если шина  обтекается током I с частотой  .

 

 

Параметры среды:  ,  . Принятое допущение

приводит к уравнению Гельмгольца (индекс х в дальнейшем опустим) относительно вектора электрической напряженности

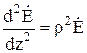
где

.

Решением уравнения Гельмгольца является совокупность экспоненциальных функций

Запишем общее решение для  , используя второе уравнение Максвелла

.

Поскольку в рассматриваемом случае  , то

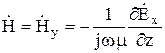
С учетом

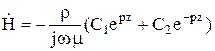
Далее отыщем постоянные интегрирования  и  . Поскольку исследуемое поле обладает симметрией 

,

следовательно, из имеем

.

Очевидно, что последнее равенство справедливо, если

.

Тогда с учетом условия симметрии

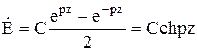
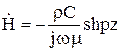
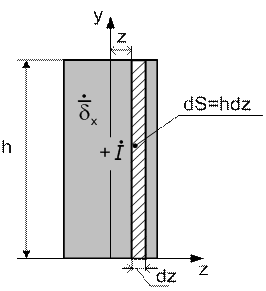
Постоянная интегрирования C пропорциональна заданному в шине току I.Выделим некоторый участок dS=hdz(рис.32). Тогда

.

 

 

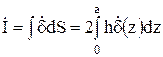Учтем далее, что  и получим

.

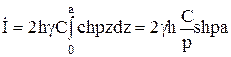Отсюда находим

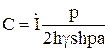
В итоге окончательные выражения для электрической напряженности  имеет вид:

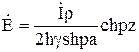
Для магнитной напряженности  :

.

 

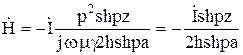Рассмотрим два варианта:

1)При  ,  , и тогда

.

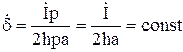Таким образом при этих условиях ток равномерно распределяет по шине и поверхностный эффект не проявляется. По мере роста частоты картина изменяется, поскольку с ростом параметра (ра) увеличивается неравномерность распределения тока по сечению шины.

Кроме того, на поверхности шины

,

что соответствует закону полного тока.

2) При 

,

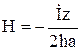т.е. при слабо выраженном поверхностном эффекте  изменяется практически по линейному закону. С ростом (ра)начинает проявляться поверхностный эффект.

Магнитный поверхностный эффект.Физическую сущность магнитного поверхностного эффекта можно пояснить на примере катушки с сердечником из литой стали.

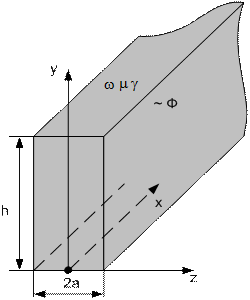
На рис. 33 представлен фрагмент шихтованного сердечника в виде стального листа толщиной 2а и высотой h, обтекаемого магнитным потоком  .

 

Найдем количественные соотношения, характеризующие поверхностный эффект в стальном листе высотой h, толщиной 2а и теоретически бесконечной протяженности.

Рассчитаем распределение магнитного и электрического полей в листе (или шине) при условии  . Данное условие позволяет существенно упростить задачу, так как в этом случае практически по всему сечению листа вектор магнитной напряженности  направлен по оси х

,

а электрической напряженности — по оси у

.

Легко показать, что при оговоренных условиях

,

.

Будем решать задачу относительно вектора  . В синусоидальном поле вектор  удовлетворяет уравнению Гельмгольца  , где  .

Уравнение Гельмгольца для  в декартовых координатах имеет вид

,

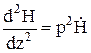а его решение, как и ранее, определяется линейной комбинацией экспоненциальных функций

Вследствие четной симметрии  имеем

.

Отсюда следует, что

Принимая, что

для магнитной напряженности, получим

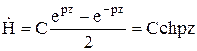
Используя первое уравнение Максвелла, запишем общее решение для вектора  . В рассматриваемом одномерном варианте

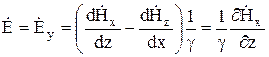
Итак, решение для электрической напряженности имеет вид

.

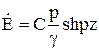Пусть, например, задано значение магнитного потока в листе. Выберем в листе полосу и запишем выражение для магнитного потока в листе

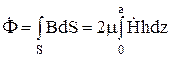
Сделаем подстановку и получим

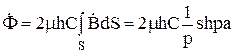
Из этого выражения определим

.

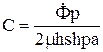При исследовании поверхностного эффекта в стальных листах удобно задаваться не потоком в листе, а средней индукцией в нем, т.е.

.

В этом случае постоянная С будет

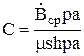
Далее получаем:

,

.

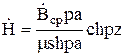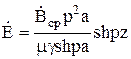С учетом того, что

,

запишем другое выражение для 

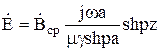
Рассмотрим два варианта:

1)  , при этом значения  ,  . Это случай неявно выраженного поверхностного эффекта, когда стальные пластины считаются «прозрачными»:

,

.

Как видно, электрическая напряженность и плотность вихревого тока в такой пластине распределяются по линейному закону. Магнитная напряженность

.

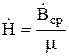В прозрачной, пластине поток равномерно распределяется по ее сечению.

2)  , это случай ярко выраженного поверхностного эффекта, когда глубина проникновения волны становится значительно меньше толщины листа, магнитный поток и вихревой ток вытесняются на его боковые поверхности.

 

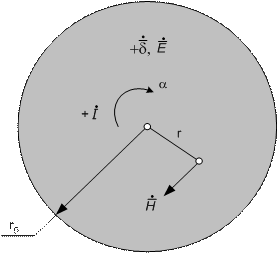
Электрический поверхностный эффект в проводнике круглого сечения.На рис. 34 изображено сечение проводника радиусом  с током  . Частота тока —  , удельная проводимость проводника —  . Зададимся целью рассчитать распределение плотности тока и вектора магнитной напряженности в проводнике и получить выражения для его внутреннего комплексного сопротивления. В силу осевой симметрии поле векторов  , ,  в проводнике и окружающем пространстве в цилиндрических координатах (r, a, z) является одномерным, при этом  ,  ,  . В дальнейшем индексы z,  а будут опущены.

 

 

 

 

 

В проводящей среде вектор электрической напряженности удовлетворяет уравнению Гельмгольца, которое в цилиндрических координатах для одномерного поля имеет вид

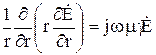
или в развернутой форме записи

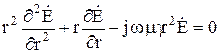
Введем новую переменную х, связанную с r линейным соотношением

.

 

где

.

.

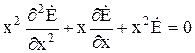Полученное уравнение является частным случаем общего уравнения Бесселя при k= 0 (k = 0, 1, 2, 3):

.

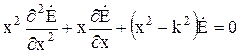Решением дифференциальных уравнений, являются специальные цилиндрические функции. В частности, к таковым относятся функции Бесселя порядка k=0, 1,2, первого и второго рода

.

Функцию  называют функцией Бесселя или цилиндрической функцией первого рода, а функцию  — функцией Неймана (Вебера) или цилиндрической функцией второго рода.

В результате при k = 0 решение уравнения представляется в виде линейной комбинации функций Бесселя и Неймана нулевого порядка

,

где  и  — постоянные интегрирования, подлежащие определению.

Из теории цилиндрических функций известно, что при х = 0

,  .

Но так как на оси провода напряженность поля не может обратиться в бесконечность, то постоянную  , следует положить равной нулю  и получить для электрической напряженности более простое решение

или, опуская в дальнейшем индекс ⁽¹⁾,

.

Запишем решение для вектора магнитной напряженности. Из второго уравнения Максвелла

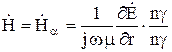
или

.

Из теории цилиндрических функций известно, что

.

Здесь  — функция Бесселя первого порядка первого рода. Таким образом, имеем:

.

Очевидно, что постоянная  , должна быть пропорциональна току в проводе I, величина которого, в соответствии с законом полного тока, связана с магнитной напряженностью поля  простым соотношением

Тогда из этих уравнений имеем

и, следовательно,

,

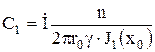где

.

Запишем окончательные решения для электрической и магнитной напряженностей. Находим:

,

.

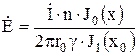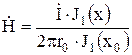Для плотности тока  имеем

.

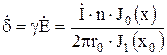Проанализируем полученные результат. Для этого рассмотрим выражения для плотности тока и магнитной напряженности при весьма малых частотах, когда поверхностный эффект практически не проявляется, и при достаточно больших частотах, при которых поверхностный эффект становится ярко выраженным.

Обратимся вначале к выражению для плотности тока:

.

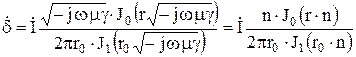Из теории цилиндрической функции известно, что при малых значениях аргумента 

, 

и, следовательно, при 

.

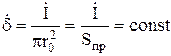Раскрываем выражение для  при  , находим

.

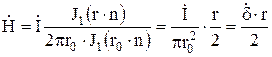Таким образом, при малых частотах, как и в стационарных режимах, ток равномерно распределен по сечению провода, а магнитная напряженность изменяется по линейному закону в функции расстояния от оси.

Рассмотрим теперь отношение значений плотности тока на поверхности провода и на его оси при больших частотах:

.

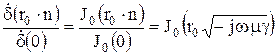Так как  , а при неограниченном возрастании аргумента  , то с ростом частоты ток вытесняется из центральных областей на периферию и при достаточно больших частотах сосредоточивается в тонком поверхностном слое.

 

Комплексное сопротивление провода.

Для расчета сопротивления провода  воспользуемся его энергетическим представлением с использованием теоремы Пойтинга

.

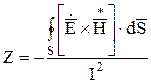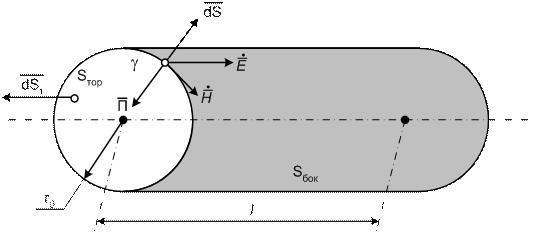
В качестве замкнутой поверхности выберем поверхность провода на длине l (рис.35), состоящую из двух торцевых

и боковой цилиндрической

поверхностей.

 

 

 

 

Как видно из рисунка, вектор Пойнтинга в проводнике направлен вдоль радиальных прямых и лежит в плоскости поперечного сечения провода, следовательно, его поток через торцевые поверхности отсутствует. На боковой поверхности вектора  и  направлены в противоположные стороны и поэтому

.

 

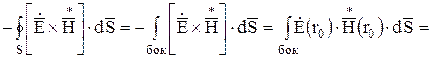
Таким образом, для расчета комплексного сопротивления провода справедливо выражение

.

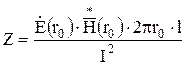Подготовим данные для подстановки в это выражение. При  имеем

,

.

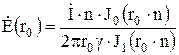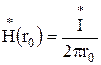После подстановки получаем окончательное выражение для комплексного сопротивления круглого провода

,

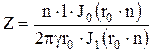где

.

Представляет интерес рассмотреть вновь частные случаи, когда частоты малы или достаточно велики, и получить соответствующие выражения для сопротивления провода. Так, учитывая, что при  ( )

, ,

находим

,

что соответствует сопротивлению постоянному току провода длиной l и сечением S.

Из теории цилиндрической функции также известно, что при  ( )

.

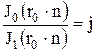Учитывая это, из (5.103) получаем

.

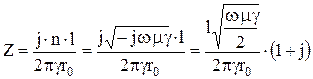При анализе плоских Е—Н волн в проводящей среде было введено понятие о глубине проникновения волны 

.

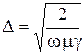С учетом этого понятия сопротивление провода становится равным

.
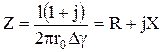