Устойчивость режимов работы нелинейной электрической цепи
Режим работы электрической цепи, содержащей нелинейные элементы, может быть устойчивым или неустойчивым. Как правило, режим работы большинства электрических цепей является устойчивым и в значительно меньшем числе случаев — неустойчивым.
Различают устойчивость «в малом» и устойчивость «в большом».
Под устойчивым режимом работы «в малом» понимают такой, при котором достаточно малое отклонение режима работы от исходного (установившегося) — независимо от того, какими причинами оно вызвано, — с течением времени уменьшается и система возвращается в исходное состояние.
При неустойчивом режиме работы «в малом» достаточно малое отклонение с течением времени увеличивается и система не возвращается в исходное состояние.
Устойчивым режимом работы «в большом» называют такой режим работы, при котором система, получив достаточно большое начальное отклонение, возвращается в исходное состояние после прекращения действия возмущения.
Если при достаточно большом отклонении от исходного состояния после прекращения действия возмущения система не возвращается в исходное состояние, то ее называют системой, неустойчивой «в большом».
Различие между устойчивостью «в малом» и устойчивостью «в большом» можно проиллюстрировать с помощью рис. 17.1, а. На этом рисунке изображены желоб с помещенным в нем шариком. Если шарик толкнуть так, что он переместится из положения 1 в положение 2, а затем предоставить его себе самому, то под действием силы тяжести шарик возвращается в исходное положение (положение равновесия). Если шарик толкнуть с большей силой, то он пройдет через положение 3 и выскочит из желоба. Таким образом, система (рис. 17.1, а) устойчива «в малом» и неустойчива «в большом».
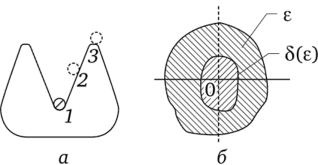
Рис. 17.1
В литературе можно встретить также термин «устойчивость по Ляпунову». Системой, устойчивой по Ляпунову, называют систему, для которой можно указать область допустимых отклонений (область 8(e) на рис. 17.1, б) от состояния равновесия (точки 0), для которой ни одно из движений, начинающихся внутри области 8, никогда не достигнет границ некоторой заданной области е.
Размер и форма области 8 зависят от размера и формы области е.
В нелинейных электрических цепях в общем случае возможны следующие режимы (типы движения):
1) состояние равновесия;
2) периодическое движение при отсутствии в системе источников периодической ЭДС (тока) — автоколебания;
3) периодическое движение с частотой источника периодической ЭДС (тока) — вынужденные колебания;
4) резонансные явления на высших, низших и дробных гармониках;
5) квазипериодические (как бы периодические) процессы по типу автомодуляции, а также ряд других, более сложных типов движений.
Каждый из этих режимов (типов движений) может быть исследован на устойчивость.
В большинстве практических задач производят исследование устойчивости «в малом». Исследование устойчивости «в большом» производят путем анализа хода интегральных кривых на фазовой плоскости или путем использования второго метода Ляпунова. Основы теории устойчивости были разработаны крупнейшим русским математиком А. М. Ляпуновым в 1892 г. и изложены в его книге «Общая задача об устойчивости движения».