
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
ис. 33. Перехiд вiд однi¹¨ тра¹кторi¨ до iншо¨ вiдповiдно до розбиття |
||||||||||||||||||||||||
часового iнтервалу. |
àêèì |
|
чином |
|
|
уду ймовiрностi через без |
||||||||||||||||||
|
Ми означили |
|
|
|
||||||||||||||||||||
межн кратний iнте |
|
|
|
. Ò |
|
|
|
|
|
÷å èé iíòå ðàë íàçè àþòü êîí- |
||||||||||||||
iíòå |
рал записують щетра¹кторiак: é |
|
|
|
|
|
|
|
|
|
||||||||||||||
що значення цього iíòå |
|
ðàëà ознае залежить вiд способiв розбиття |
||||||||||||||||||||||
тинуальним, або у кцiон ль |
|
èì,ïëiíте ралом. Ми |
äiâà¹ìîñü, |
|||||||||||||||||||||
часового промiжку трал |
|
|
|
|
|
Z |
|
|
на елементарнi iнтервали. Цей |
|||||||||||||||
çà |
|
|
K(b, a) = |
|
e êòîðiÿD[x(t)]. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ S[x(t)] |
|
|
|
|
|
|
|
||
|
звукийшляхУнаслiдокметодуорсиамиуливолiчний. .iнтеадитивностiЗiскрзаписзаноголiв¹ птункцi¨стðà¹остозрозудi¨скороченимiло,и,абочометозаписомуцейдупiдхiдiнтепопередралiвма¹- |
|||||||||||||||||||||||
íÒüî¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = S[b, a] = Zab L dt = Zac L dt + Zc b L dt, |
|
|||||||||||||||||||||
можемо записати амплiтудуS[b, a] = S[b, c] + S[c, a] |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
K(b, a) таким чином: |
|
|||||||||||
|
|
K(b, a) = |
lim |
|
1 |
|
|
|
dx1 |
... |
dxc−1 |
|
|
|
|
|
||||||||
|
|
|
A Z |
|
A |
|
|
|
|
|
||||||||||||||
|
|
|
N |
→ |
0 |
|
|
|
Z |
|
A |
|
|
|
|
|
||||||||
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
→∞ |
|
|
|
|
|
... Z |
|
|
|
|
|
|
|
|||||||
272 |
|
|
|
dx |
|
dxc+1 |
|
dxN |
1 |
|
i |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
× |
Z |
|
|
c |
Z |
|
|
|
|
|
|
A− |
|
e ~ S[x(t)] |
|
|||||||
|
|
|
|
A |
|
|
|
A |
|
|
|
|||||||||||||


ðiâíяння:iсть для хвильово¨ óíêöi¨, можнаb. Викнаписатиористовуючиакеiнтепопереднюральне |
||||||||||
хвильовоюЗа сво¨м змiстомункцi¹юамплiту. Фiкс ючида Kпочаткову(x , t ; x , tточку) ¹ íi÷èì iíøèì, ÿê |
||||||||||
|
|
|
|
|
b |
b |
|
a |
|
a |
мемо цей вираз як хвильов ункцiю |
|
|
|
|
a, розглядати- |
|||||
яка залежить вiд змiннихψ(x t |
) =òî÷öiK(x |
, t |
; x |
a |
, t |
a |
), |
|||
|
|
b |
b |
b |
b |
|
|
|
||
|
перехiдЯкперейтивiдψ(xb, tb) = Z |
dxc K(xb, tb; |
xc |
, tc)ψ(xc, tc). |
||||||
ìî |
|
хвильово¨дорiвнянняункцi¨Шрединв моментера? З цi¹ючасу метою розгляне- |
||||||||
iншийДомови |
åíò ÷àñó |
|
|
|
|
|
|
|
t до ¨¨ значення |
|
|
ìось щодоtпозначень+ ε при ε.→Нехай0. |
|
|
|
|
|||||
|
|
|
|
|
|
tc = t, tb = t + ε, xb = x, |
||||
вигляду:Тепер iнте ральне рiвняння для хвильово¨ ункцi¨ набира¹ |
|||||||||||||||||||||||||||||
xc = y. |
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нялиде ядро, вiдповiдноψ(x, t +äîε) = |
dy K(x, t + ε; y, t)ψ(y, t), |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
розбиття часового iнтервалу, яке ми прий- |
|||||||||||||||||||||||||
|
|
|
|
|
A |
|
|
|
|
|
|
÷àñòèíêè, |
2 |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
~ |
|
|
|
|
ε |
|
|
|
|
||||||||||||||
i îòæå,K(x, t + ε; y, t) = |
1 |
exp |
i |
εL |
|
|
x − y |
, |
x + y |
, t + |
ε |
|
, |
||||||||||||||||
|
|
ε→0 Z A |
~ |
|
|
|
|
ε |
|
|
2 |
|
|
2 |
|
|
|||||||||||||
|
|
|
∞ |
|
|
|
|
|
|
|
− |
y |
|
|
|
ùî, tðóõ+ à¹òüñÿψ(y,â tïîëi). |
|||||||||||||
ψНехай(x, t + далiε) = ункöiÿexpËà ðàíæàεL |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
dy |
|
i |
|
|
|
x |
|
|
x + y |
|
ε |
|
|
|
|||||||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
U (x, t), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mx˙ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
òîäi |
|
|
|
|
L = |
|
|
|
− U (x, t), |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||
|
ε |
2 |
|
|
|
2 |
|
|
|
|
2ε2 |
|
|
|
− |
|
2 |
|
|
|
|||||||||
274 L |
x − y |
, |
x + y |
, t + |
ε |
= |
m(x − y)2 |
|
|
|
U |
x + y |
, t + |
ε |
. |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||

Для того щоб просунутись äалi, використа¹мо iнтå ðàëè:
∞ |
|
|
|
|
|
∞ |
|
|
1 |
|
|
|
Z |
2 |
dz = r |
π |
|
Z |
2 |
|
|
π |
|
||
e−αz |
α |
, |
z2e−αz |
dz = |
2α r |
α |
, |
|||||
−∞ |
|
|
|
|
|
−∞ |
|
|
|
|
|
|
очевидно, iнтеα =ðàëè−içíàõ+ δ,непарнимиδ > 0, степенями |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Çâiäñè ïðè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z дорiвнюють нулевi. |
||||||||||
|
δ → 0 |
|
|
|
одимо потрiбнi нам iнте рали ма¹мо: |
|
|
|
|
||||||||||||||||||||
|
∂ψ(x, t) |
|
|
|
1 |
|
|
|
2~ε |
|
|
|
|
|
|
|
|
1 ∂2ψ(x, t) 2~ε i |
|||||||||||
ψ(x, t) + ε |
= |
|
|
|
|
|
|
√iπ |
|
|
ψ(x, t) + 0 + |
||||||||||||||||||
∂t |
|
|
|
A r m |
|
|
|
|
2 ∂x2 |
|
m 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
iîчастинажники прирiвнянняоднаковихдорiвнюваластепеняхправiй, |
|
|
|
|
||||||||||||||||||
обхiдноДля прирiвнятитогощоблiва−ìí~ |
εU (x, t)ψ(x, t) . |
|
|
|
|
|
íå- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
r |
|
2~εiπ |
= 1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
A |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂ψ(x, t) |
|
|
|
~ |
|
|
∂2ψ(x, t) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Перше рiвнÿííÿ âèзнача¹ íàì ñòàëу величину |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
∂t |
|
|
|
= |
|
2m ∂x2 |
|
|
− ~ U (x, t)ψ(x, t). |
|
|
|
|
|
|
|||||||||||||
муостаточнотут спос бiiксу¹морозбиттявизначечасовогоняа |
плiтуди. ймовiрностейОтже,A притимприйнятосамимми |
||||||||||||||||||||||||||||
|
|
|
|
|
|
iíòå |
|
|
|
|
|
|
|
|
iíòåðâàëó |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
систем, |
|
|
|
K(b, a) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
∂ψ(x, t) |
|
|
|
|
|
|
~2 ∂ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
квантичнийнеовоюкартинкаметодущомеханiкоюапаратФейнманаперевагквантово¨якрiвнянняакимШрепiдхiдiнтепоняттяммехинШанiки,ераФейнманаедин.заÿêòðàiнтзбагачу.¹кторiяминеОтже,рали. минеПростозазлишевстановилихвильовоюшляхамице¨¨маще-, |
|||||||||||||||||||||||||||||
276темоднаЦе'язокСпецiальних¹з ~ |
∂t |
|
|
|
= −2m ∂x2 |
+ U (x, t) ψ(x, t). |
|
|
|
|
|
|
|||||||||||||||||
|
iíøå, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i отриму¹мо |
|
|
|
|
|
|
|||
чводититерахезДругебагдля¨¨атокрозррiвнянняратнийкретнихахункипомножичисельмодельнихðàëìîèìè.ðÖå,íààëiìåâсво¹юдамизадаючичергою,на сучаснихда¹ларанжiанзмогукомïðî'þ.-
але й наше класичне мислення в намаганнi |
|
|
|
|
|
квантовi за |
|||||||||||||||||||||||||||||||||||
|
|
|
|
Тут цiкаво пригадати концепцiю ене Декартзбагнутищодо побудови |
|||||||||||||||||||||||||||||||||||||
êîíè. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Декартом, нам невiдо |
|||||||||||||||
теорi¨ сп стережуваних явищ. |
|
Áîã |
|
|
|
||||||||||||||||||||||||||||||||||||
ìî, ÿêèì iç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
запров д |
¹ |
|
есь iзичне |
|||||||||||||||||||||||
айзенбер |
|
Шредин ер тсуперечатьФейнмОскiльки,àí ¹ iлюстрацiями цi¹¨ декарт |
- |
||||||||||||||||||||||||||||||||||||||
ñò |
|
|
потрiбноНьютон,для пояснення |
|
|
|
|
|
|
|
íèõ |
ÿâèù, |
âií |
áóâ |
|
äíùî |
|||||||||||||||||||||||||
явище, |
|
|
|
йнезчисленнихтеорi¨,що |
|
|
|
|
|
äîñâiäó, ìîæóòü áóòè |
åîäí |
|
|||||||||||||||||||||||||||||
значними. Мабуть, кар инкиспособiв |
тово¨ механiки, ÿê |
винайшли |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
÷íiñòü |
òåîði¨ áåç áóäü-ÿêèõ ãiï |
òåç, |
|
рунтуючись |
ëèøå |
çà äîñëi |
|||||||||||||||||||||||||||||||
во¨ концепцi¨. |
|
|
|
|
|
|
|
був протилеж |
|
|
погляд |
. оворячи, |
|
||||||||||||||||||||||||||||
íå |
|
|
|
|
|
|
|
|
|
|
|
|
ÿê |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
бративiдомо,розгляду |
ðè÷è |
|
áiëüøå, |
æ |
|
|
ÿêèõ |
|
|||||||||||||||||||||
дi. Викликом цим поглядамспостережува¹ дв як природа |
|
латих, й узагалi |
|||||||||||||||||||||||||||||||||||||||
çíàîê |
|
|
|
|
|
|
|
|
|
|
механiки крiм рiвнянь Ньюто а, ма¹мо рiвня ня |
||||||||||||||||||||||||||||||
|
рпускулярно-хвильовий дуалiзм, зрештою, яксвiтдекiльк |
|
карти- |
||||||||||||||||||||||||||||||||||||||
ßê . . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ла ранжа,класично¨анонiчнi рiвняння амiльтона, рiв яння амiльтоíà |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
обiВ дступ. |
|
|
адки квазiкласичного |
|
|
|
|
|
|
|
. |
|
äîì |
Áîðà |
||||||||||||||||||||||||
|
|
|
|
Ìè çíà¹ìî, ùî êâàзiкласичне квантува |
|
|
|
||||||||||||||||||||||||||||||||||
U0/ cos (x/a) |
U = U0/ch (x/a) |
|
|
|
Ÿ23 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Зоммерармонiчногоельда да¹ точнi вирази для рiвнiвантуванняðåçó åð i¨ìåòî |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
квазiкласичнихюгкйгпоказати, |
дляосциляторапотенцiлу.ТочнийМорзе |
|
|
ëü àò |
En |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
держу¹мо,атома водяк- |
|||||
|
|
|
|
|
|
|
|
− |
|
p |
|
|x|- |
|
|
|
|
− |
|
|
|
|
|
|
U = U1e−2x/a |
|
U2e−x/a |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и осцилятора x4 |
|
|
|
|
|
|
|||||||||||||||||||
|
приклад для |
|
|
|
|
|
|
|
|
(2n + 1)]2~ /8ma2. Äëÿ |
iнших задач, |
||||||||||||||||||||||||||||||
En |
|
= |
|
|
|
|
[U2 |
2ma2/~2U1 |
|
|
|
− |
|
|
|
||||||||||||||||||||||||||
å ó™ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òî÷íi, для яких iз квазiкласичних,тенцiалiвакогозбiгуви- |
|||||||||||||||||||||
ðàçiâ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
щедляттiвдинужецiкавийнема¹.клас зада |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
En можнавиразах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
витдляягти |
|
резульотрима¹моати.Зкрема, |
îëè |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
En, обчислених для п |
|
|
|
|
U = |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
2 |
|
2 |
|
|
|
i Приклад 1 до нього), |
|||||||||||||||
|
|
|
|
|
. Òàêå æ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
âåë ÷èíó |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
(äèâ. |
|
|
||||||||||||||||||||||||
òàò |
|
|
|
|
|
|
|
|
|
|
перенормування параметрiв, то |
|
|
|
|
|
|
точнi резуль- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
U0 çàìiíèòè íà U0 |
+~ /8ma |
|
|
|
U1, Uточний2 ï òåíöiàëó U = |
|||||||||||||||||||||||||
U1/ sin2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
(x/a) + U2/ cos2(x/a), 0 ≤ x/a ≤ π/2 ä๠|
|
|
|
резульматимат |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
p |
|
1 |
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
≤ |
|
|
|
≤ |
|
|
2 |
2 |
|
|
|||||||
En |
|
= [ |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 + 8ma |
U1/~ + |
|
|
1 + 8ma U2/~ + 2(2n + 1)] |
~ |
/8ma |
à |
||||||||||||||||||||||||||||||
ïîëi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(сталуx/a) + U ctg(x/a), 0 |
|
x/a |
|
π ïîòðiáíî ïåðå |
||||||||||||||||||||
|
рмовуватиU = U ëèøå/ sin |
|
|
||||||||||||||||||||||||||||||||||||||
ìî |
|
|
|
|
чний результат: |
|
U1, але не змiнювати сталу U2 |
|
|
- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
En = ( |
1 + 8ma2U1/~2 |
+ 2n + 1)2~2/8ma − |
|||||||||||||||||||||||
äî2 |
|
розкриття цi¹¨2 |
загадки2 |
|
|
|
|
суттю2 2 öèõ2.перенормуваньНеважкрозгледiти¹додаванключ277- |
|||||||||||||||||||||||||||||||||
U |
|
/( |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
+1) ~ |
/2ma |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
1 + 8ma U1/ +2n |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
доданкахкласнавп тåñòíöiàëîìèчнiйпотенцiалуiншiмежi.Длÿкiпiдтверджспричинюютьякiвиявл2 åííÿ2ютьдонашогомалiсталихсуперсиметоливань,кмножсновкуванизацi¨iюяикiв,системиможнасупертих-
я енер i¨ нульовихприклади,оливань ~ /8ma
|
|
|
|
|
|
|
åð |
не брати(див. |
||
Ÿ23)уваги.Якщопохiдно¨уWквазiкласичномуточнорозв'язуютьсрозрахункуметодомрiвнiвакто |
|
|
|
|||||||
Áîðà |
|
|
W ′ |
|
W |
|
|
|
U |
|
|
|
|
|
|
|
|
|
якiвониалом¹порочася, |
||
|
|
|
|
|
ченостейхвильтина¹i,алiякийпранульовихщеiйзв'язу¹айзенбердначастинiкзагадкаумова,звеликихпотенцоча.квантуван |
|
||||
|
|
|
|
|
à |
|
|
|
|
|
|
|
|
|
невизумовопртим,вхузульвирдятьщое |
|
|
|
|
|
|
îовоеннямКвазiкласичнийдержу¹моЗоммервжпринципуквазiкласичнеахточнiельдаованi |
|
|
|
|
|
|
||||
äæ |
|
|
|
|
|
|
|
|
|
|
òê |
|
|
|
|
|
|
|
|
|
|
|
âiä |
|
|
|
|
ву, числовеункцiюзнач обтонняякихактичнозале |
||||
ñòàëiæèòü |
|
граничних |
|
ν |
|
|
|
|
||
|
|
наведенiпринес |
|
|
|
|
|
ðå |
||
|
|
вищззовнi,å перенормуванняíàзближточно¨ теорi¨да¹,.парамякДляiдомо,трiв пт чнийтенцiалукванто |
||||||||
зультат,вихеважливiчиселν ïðè |
|
|
|
|
|
|
|
|
||
близьких |
|
n 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
- |
íапрошуiхормуува¹моiвнiв.¹тьсяДлясталiдоособливоточнихмiркуванняцьоговипедля. Такенормовуазiвосновногощоäлясп¹морiвнiвсобстанупараметриванняз. ераходженняЗíàâi¨ ажливезденихквазiклпотеточнихцiдлязагсичлуадокнижàáî |
||||||||||
ñновного стану на т |
величини, якi принесуть точджуютьсенер iю |
|||||||||
квазiточно |
ν |
|
|
|
|
|
|
|
||
ðî¨íèìè |
|
|
E0 |
|
|
|
|
званихякийстя - |
||
|
|
|
|
|
|
|
óçãîЗапропонованаiключаприкладах,врiацiйночисель |
|||
|
|
|
|
|
|
|
йденими |
|
|
|
|
|
|
|
|
|
ðàлрезультатiв,åнямтних.д, |
|
|||
|
|
|
|
|
|
здимо |
|
|
|
|
|
|
|
|
|
|
åí |
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
точнищопроцедурагорунту¹тьсяметоквантово¨держанiи результатами.дамиЧитперенормуваньрозв'язуванихнаакиммехпринципiчрозв'язкулегк,спiкидлясобомперекона¹тьсдовiдповiдностiсврiвняння¹всiхвгадуваннядеякимделей¹ювиразирiвнiвчергоючи,ШрузагальндужееíБнапритåîзнахдинрачнихкондобi¨,. |
|
|
|
|
||||||
|
|
|
|
|
|
|
À Â À VI |
|
|
|
|
||
Ÿ 32. |
|
МОМЕНТ КIЛЬКОСТI УХУ |
|
|
|||||||||
|
|
дставляючиповороту |
i момент |
îñòi ðóõó |
iì- |
||||||||
сичного |
иразу, |
нього, |
|
кiлькоординат |
|||||||||
момент кiлькостiОператорху або момент iмпульсу, виника¹ як iнте |
ðàë |
||||||||||||
Ìè |
|
|
èëè |
|
ератор моменту кiлькостi руху виходячи з кла |
||||||||
|
ââîiäïîâiä |
оператори. У класичнiй механiцi, |
ÿê âiäîìî, |
||||||||||
р льсiв,ху пов'язаний з iзотропi¹ю простору. Цезамiстьакож ¹ справедливим |
|||||||||||||
пуквантовiй еханiцi. |
|
|
|
|
|
|
|
|
|||||
Iнту¨тивно зр зумiло, що властивостi будь-яко¨ замкнено¨ i |
|||||||||||||
зично¨ |
системи |
не залежать вiд того, |
|
якого боку ми дивимось |
|||||||||
на не¨. Це наслiдок того, що всi напрямки |
просторi |
еквiвален |
|||||||||||
|
к ж т , що простiр ¹ |
|
|
|
. Îòæå, |
|
|
||||||
iльтона |
|
î¨ |
|
|
не повинен змiню |
тись при ¨¨ по оротах |
|||||||
ÿê öiëîãî |
акбудь-який кут навколо довi |
ьно¨ осi. Нехай при |
àêî |
||||||||||
|
|
|
|
|
|
|
|
|
|
ëоваежить хвильоператорнабува¹ункцiя |
|||
тнимиуповоротiзмiню¹тьсрадiусистеми-вектор r, вiд якiзотропнимгоза |
|
|
|||||||||||
ψчення(r), |
|
|
|
я на величину δr, а хвиль |
óíêöiÿ |
|
çíà- |
||||||
äiþ íàψíå¨(r +оператораδr). Цю змiнузмiщення:хвильово¨ ункцi¨ можна з |
бразити як |
||||||||||||
|
|
|
|
|
|
|
|
(δr ) |
ψ(r). |
|
|
||
Нехай поворот здiйсню¹тьсψ(r + δríà) =êóòe |
|
|
|||||||||||
iксу¹ться диничним вектор м |
δϕ |
вколо осi, напрям як ¨ |
|||||||||||
ðîì |
|
|
|
|
|
|
|
n, що утворю¹ з радiусект - |
|||||
що величинаr кут величиноюзмiщенняθ, ÿê öå |
îбражен |
|
на рис. 35. З нього виднî, |
||||||||||
|
|
|
|
|
|
|δr| = ρ δϕ, |
|
|
|
|
|
||
Отже, вираз |
|
|
ρ = r sin θ. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|δr| = r sin θ δϕ |
|
|
279 |
||||
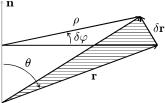
можна тра як модуль що ¹ результатом вектор-
ного добутêтувативектора δϕ = nδϕвектора,радiус-вектора r:
δr = [δϕ r].
Далiис.35ма¹мо.Операцiяяд простихповоротуперетвореньна кут δϕ навколо осi з нарямком n.
êiëüê |
i |
ˆ |
де оператор(δr ) = ([δϕ r] ) = (δϕ[r ]) = ~ (δϕ[rpˆ]) = |
~ |
(δϕ L), |
ˆ ˆ
¹величинимîментператоромТепер.ма¹морбiтальногоментiмпульсу,моменL÷àñ= ò[rîópùå] говорятьостiрухупросто.Iнша назвакутовийцi¹¨
де оператор |
|
|
|
|
ˆ |
|
|
ψ(r + δr) = Rδϕψ(r), |
|
||||||
будемо називати опе |
ˆ |
|
|
i |
ˆ |
|
|
|
~ |
|
|
|
|||
îðîì ïîâîð(îòóδϕ Líà) êóò |
|
||||||
|
Rδϕ = e |
|
|
|
|
|
|
прямком |
|
|
|
|
|
δϕ навколо осi з на- |
|
ðàòненнийповтореннякут повороту |
елементарний |
||||||
кут да¹ поворотn. Багатокнаскiнч |
|
|
|
|
|
|
|
|
|
|
|
|
ϕ: |
|
|
|
ˆ |
i |
|
ˆ |
|
|
|
280 |
~ |
ϕ(nL) |
. |
|
|||
Rϕ = e |
|
|
|
|
|
||

|
Твердження про те, що вл стивостi |
|
системи не зале |
||||||||||||||
жать вiд поворотiв, оз |
|
ча¹, що з хвильового рiвняння Шредин- |
|||||||||||||||
оператордля |
|
|
|
|
|
|
|
|
ього оператором |
|
|
||||||
ψ(r) |
äi¹þ íàсамимí |
|
|
замкнено¨ˆ |
|||||||||||||
äëÿ |
|
|
|
|
|
|
|
|
|
|
|
|
Rδϕ отриму¹мо рiвняння |
||||
|
ψ(r + δr) |
ç òèì |
|
|
|
|
гамiльтонiан |
ˆ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
H. А це означа¹, що |
||||
|
|
|
ˆ комуту¹ з оператором повороту ˆ |
||||||||||||||
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
Rδϕ. Справдi, ма¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
∂ψ(r) |
ˆ |
|
|
|
|
а пiсля дi¨ оператора повоi~ ðîòó |
= Hψ(r), |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
i~ |
∂Rδϕψ(r) |
ˆ |
ˆ |
|
|
|||||
àáî |
|
|
|
|
|
|
|
∂t |
|
= RδϕHψ(r), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂Rδϕψ(r) |
|
|
|
|
|
|
|
|
|
|
|
|||
Çâiäñè |
зновуi~ |
отриму¹мо,ˆùîˆ |
ˆ ˆ |
|
|
ˆ ˆ |
|||||||||||
|
|
|
∂t |
|
|
= |
|
RδϕH − HRδϕ |
ψ(r) + HRδϕψ(r). |
||||||||
|
|
|
|
|
|
öié L íà îñi x, y, z: |
|
|
|
||||||||
за умови, що комутатор~ |
∂ψ(r + δr) |
ˆ |
|
|
|
||||||||||||
|
|
|
∂t |
|
= Hψ(r + δr) |
||||||||||||
|
|
чином, |
|
|
значить,ˆ ˆ |
ùîˆоператорˆ |
|
||||||||||
À |
цевiсь свою чергу |
|
|||||||||||||||
|
|
|
|
|
RδϕH |
− HRδϕ |
= 0. |
|
|||||||||
ðîì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проекцi¹юH уту¹ з операто |
||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
ˆ |
íó L. Точнiше,знапрямкаоìiльтонiан H комуту¹ з |
L íà äîâiëü- |
||||||||||||||||
з акиможною з прое |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|||||
|
|
n. Ми держу¹мо тим самим, що H комуту¹ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
|
|
|
|
|
|
ˆ |
еннiвиплива¹раторiвкiлькостiˆ 1. проекцi¨законрухуˆ¹збермоментуiнтеˆ женняраламикiлькостiмоменруху-. |
|||||
|
кiлькВипишiмовзоорiзотростiдинатномурухуявнийï îекцi¨с(теоремавиглядпмоментузображосторуНетер)оп |
|
|
[Lz , H] = 0. |
|||||||||||||
рухутуОтже,Т |
[Lx |
H] = 0, |
|
|
|
|
[Ly, H] = 0, |
|
|||||||||
Lx ñ=. 166−i.~ |
y ∂z |
− z ∂y |
, |
|
|||
1Див. Ÿ17 та виноски ˆíà |
|
|
∂ |
|
∂ |
|
281 |
|
|
|
|
|
|||
