
33_Rezhimy_post_i_sin_toka_v_LETs_2014
.pdf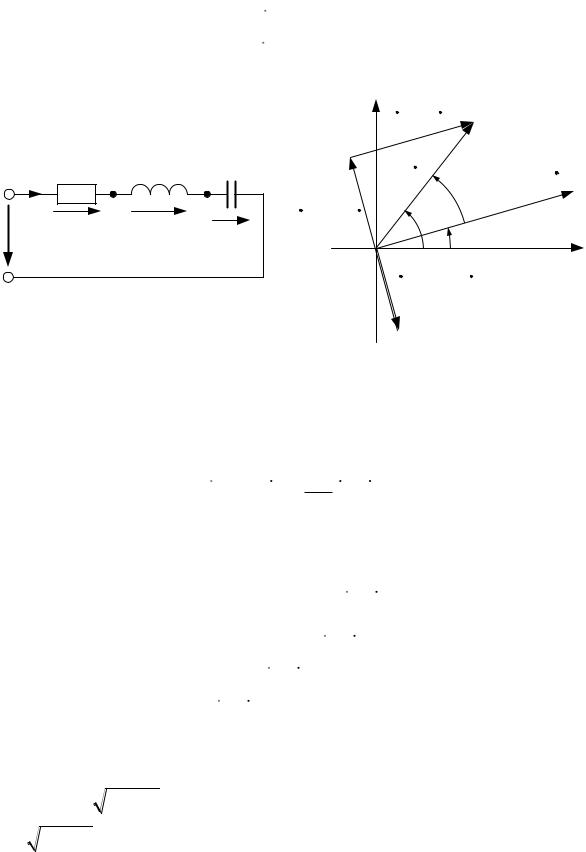
U Ue j ; |
|
|
(3.68) |
|
|
I Ie j . |
|
|
|
|
|
|
|
|
|
|
+j |
Ur = rI |
|
a |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
c |
|
|
|
a |
i |
r |
c |
L |
d |
C |
|
U |
φ |
I |
|
|
|
|
|
|
|
|
|
||
u |
|
ur |
|
uL |
|
uC |
UL = jxLI |
β |
α |
|
|
|
|
|
|
|
|
|
|||
b |
|
|
|
|
|
|
b |
|
|
+1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
UC = –jxCI |
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
а |
|
|
|
|
б |
|
Рис. 3.11. Электрическая цепь с последовательным соединением r, L, C
Уравнению (3.66) в комплексной форме соответствует уравнение
rI j LI j 1C I U ,
которое преобразуется в следующей последовательности:
|
|
|
|
1 |
|
r j L j |
|
|
I U ; |
||
|
|
||||
|
|
|
C |
||
|
|
|
|||
|
|
|
|
I U ; |
|
r jx |
L |
jx |
|
||
|
C |
|
|
||
r jx |
I U ; |
|
|
||
|
|
|
|
|
|
ZI U ,
где x xL xC – реактивное сопротивление;
(3.69)
(3.70)
|
|
|
|
e j arctg |
x |
|
Z r jx |
r2 x2 |
|
ze j – комплексное сопротивление цепи; |
|||
r |
||||||
|
|
|
|
|||
z |
r2 x2 |
– полное сопротивление, или модуль комплексного сопро- |
||||
тивления;
90

arctg rx – аргумент комплексного сопротивления, представляющий со-
бой угол сдвига фаз между входным напряжением и током.
Установленные здесь закономерности имеют общий характер и сводятся к следующему:
индуктивное и емкостное сопротивления в состав общего реактивного сопротивления входят с разными знаками (индуктивное – с плюсом, емкостное – с минусом);
модуль комплексного сопротивления есть полное сопротивление; аргументом комплексного сопротивления всегда является угол сдви-
га фаз между соответствующими напряжением и током.
Результатом решения задачи является комплексное действующее значение тока (комплекс тока)
I |
U |
, |
(3.71) |
|
Z |
||||
|
|
|
по которому записывается мгновенное значение тока.
Векторная диаграмма, представленная на рис. 3.11, б, построена в масштабах действующих значений тока и напряжения (модулей комплексов). Общей величиной для всех элементов является ток i, поэтому вектор тока I на данной диаграмме является исходным, или базовым.
Векторы падений напряжения ориентированы относительно вектора тока с учетом фазовых соотношений для элементов r, L и С: в сопротивлении r напряжение и ток совпадают по фазе; в индуктивности напряжение опережает ток на 90 º; в емкости напряжение отстает от тока на 90 º.
Построение топографической диаграммы обычно проводят, совершая обход схемы против направления тока, т. е. от точки b к точке a (см. рис. 3.11, б). Векторы падений напряжения на векторной диаграмме соответствуют расположению элементов на схеме. Потенциал точки b принимается равным нулю. При таком обходе потенциал исследуемой точки выше потенциала предыдущей и стрелка вектора, соединяющего точки на диаграмме, указывает направление возрастания потенциала. На рис. 3.11, б из точки b последовательно отложены векторы UC , U L и Ur . Геометрическая сумма этих векторов равна приложен-
ному напряжению U.
91

Векторные диаграммы такого типа называются топографическими векторными диаграммами. Главная их особенность – соответствие расположения векторов падений напряжений расположению элементов на схеме.
Векторная диаграмма (см. рис. 3.11, б) соответствует случаю, когда ин-
дуктивное сопротивление x L превышает емкостное |
x |
|
1 |
, поэтому па- |
|
|
|||||
L |
|
C |
|
C |
|
|
|
|
|
||
дение напряжения на индуктивности UL xLI |
больше падения напряжения |
||||
UC xC I , угол φ положителен, напряжение по фазе опережает ток и относительно входных зажимов схема воспринимается как активно-индуктивная. При выполнении условия xL xC вектор U L будет меньше вектора UC и схема относительно входных зажимов будет восприниматься как активно-емкостная, поскольку вектор напряжения U окажется отстающим по отношению к току I.
Возможен и частный случай, |
когда xL xC |
и UL UC . Угол сдвига фаз в этом |
||||||
случае равен нулю и схема попадает в режим резонанса напряжений. |
|
|||||||
Схема с параллельным соединением элементов (рис. 3.12, а) требует при- |
||||||||
влечения понятий комплексных проводимостей. |
|
|
|
|
||||
i |
|
|
|
+j |
|
|
U |
|
|
|
|
|
|
|
|
||
r |
L |
C |
|
|
|
|
|
|
u |
|
|
|
|
I |
|
IC |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
i r |
|
iL |
iC |
|
|
I r |
IL |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
б |
+1 |
|
|
|
|
|
|
|
||
Рис. 3.12. Электрическая цепь с параллельным соединением r, L и С
Уравнение для мгновенных значений записывается по первому закону
Кирхгофа: |
|
|
|
|
|
|
|
ir iL iC i |
|
(3.72) |
|||
или |
|
|
|
|
|
|
ug |
1 |
udt C |
du |
i , |
(3.73) |
|
|
L |
dt |
||||
|
|
|
|
|
||
где g 1 r.
92

Уравнение в комплексной форме имеет вид:
Ug |
1 |
U j CU I. |
(3.74) |
|
j L |
||||
|
|
|
Векторная диаграмма токов показана на рис. 3.12, б. Этапы преобразования уравнения (3.74):
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
j C U I ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
j L |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
j |
|
|
j C U I ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
g |
|
j b |
b |
U I ; |
(3.75) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
g jb U I ; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
YU I. |
|
|
|
||||
Здесь появились новые величины: |
|
|
|||||||||||||||
b |
1 |
– индуктивная проводимость; |
|
||||||||||||||
|
|
|
|||||||||||||||
L |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
bC C – емкостная проводимость; |
|
|
|||||||||||||||
jb |
|
j |
1 |
|
|
|
1 |
|
– индуктивная проводимость в комплексной форме; |
||||||||
|
|
|
|
||||||||||||||
L |
|
|
L |
|
|
j L |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
jbC j C – емкостная проводимость в комплексной форме; |
|
||||||||||||||||
b bL bC – реактивная проводимость; |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
j arctg b |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Y g jb |
|
g 2 b2 |
e |
g ye j |
– комплексная проводимость; |
|
|||||||||||
y |
|
g2 b2 |
|
|
– полная проводимость как модуль комплексной проводи- |
||||||||||||
мости.
Любая комплексная проводимость выступает как величина, обратная комплексному сопротивлению. Для отдельных элементов
jb |
|
|
1 |
|
; |
||
|
|
|
|||||
|
C |
|
|
jxC |
|
||
|
|
|
|
(3.76) |
|||
|
|
|
|
|
1 |
|
|
jb |
|
|
. |
||||
|
|
||||||
|
L |
|
|
jxL |
|
||
|
|
|
|
|
|
||
93

В общем случае
Y |
1 |
; |
|
||
|
Z |
(3.77) |
|
1 |
|
|
|
|
Z |
|
. |
|
Y |
|
Формулы (3.77) бывают полезны в тех случаях, когда требуется преобразовать последовательные схемы в параллельные и наоборот. Предположим, что требуется схему на рис. 3.13, а преобразовать в схему, представленную на рис. 3.13, б.
|
r |
|
|
g |
b |
|
|
|
|
L |
|
а |
б |
|
Рис. 3.13. Преобразование схем с последовательным (а) и параллельным (б) соединением элементов
Комплексное сопротивление первой схемы записывается в такой форме:
Z r j L. |
(3.78) |
Комплексная проводимость записывается как величина, обратная Z:
Y |
1 |
|
1 |
. |
(3.79) |
|
Z |
r j L |
|||||
|
|
|
|
Умножая числитель и знаменатель дроби в формуле (3.79) на комплекс, сопряженный знаменателю, получаем:
Y |
r j L |
|
r |
j |
L |
. |
(3.80) |
|
r2 2L2 |
r2 2L2 |
r2 2L2 |
||||||
|
|
|
|
|
В итоге значения проводимостей схемы на рис. 3.13, б таковы:
94
|
|
|
|
|
r |
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
; |
|
||
|
r |
2 |
|
2 |
2 |
|
||||||
|
|
|
|
|
L |
|
|
(3.81) |
||||
|
|
|
|
|
L |
|
|
|
|
|
||
b |
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
2 |
|
2 |
|
|||||
|
r |
|
|
|
|
|
||||||
|
|
|
|
|
L |
|
|
|
||||
Реализацию обратного перехода можно осуществить путем преобразования общей комплексной проводимости схемы на рис. 3.13, б в комплексное сопротивление согласно формулам:
Y g jb; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
1 |
|
|
g jb |
|
|
|
|
|
g |
|
|
|
|
b |
|
|
(3.82) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
, |
|
|
Y |
g jb |
|
g |
2 |
b |
2 |
g |
2 |
b |
2 |
g |
2 |
b |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
r |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
g |
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
(3.83) |
||||
|
|
|
|
|
g 2 |
b2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
L |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.6. Особенности применения комплексного метода для исследования разветвленных электрических цепей
Положительным свойством комплексного метода является то, что операции с комплексными напряжениями, токами, сопротивлениями и проводимостями осуществляются по тем же основным правилам, что и в случае цепей постоянного тока.
Законы Кирхгофа для цепей постоянного тока формируются алгебраическим суммированием составляющих – токов при формировании уравнений по первому закону Кирхгофа, а также ЭДС и падений напряжения при составлении уравнений по второму закону Кирхгофа.
В случае цепей переменного тока алгебраическое суммирование в действительной области применимо только для мгновенных значений, как это сделано при составлении уравнений (3.23), (3.65), (3.72). Действующие и амплитуд-
95

ные значения напряжения или тока суммируются только геометрически, на что указывают все приведенные ранее векторные диаграммы.
В комплексной форме алгебраические операции можно производить практически со всеми встречающимися при расчете электрических цепей величинами: комплексными амплитудами, комплексными действующими значениями, комплексными сопротивлениями и проводимостями. Нужно лишь правильно применять правила действий с комплексными числами.
Рассмотрим схему, изображенную на рис. 3.14, а.
I1 r1 |
L1 |
1 |
|
|
I1 |
Z 1 |
|
1 |
|
|
|
|
C |
|
|
|
|
|
|
Z 1 |
|
r2 |
|
|
|
|
|
|
|
|
Z 2 |
|
|
Z 3 |
|
|
Z 2 |
|
Z 3 |
U |
|
|
r 3 |
|
U |
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
I 3 |
|
|
|
|
I2 |
I 3 |
|
а |
2 |
|
|
|
|
б |
2 |
|
|
|
|
|
|
|
|
|
Рис. 3.14. Заданная (а) и упрощенная (б) расчетные схемы
Пусть заданы параметры элементов схемы, а также входное напряжение u Um sin t .
Ставится задача определить токи ветвей. Расчет проводится по комплексным действующим значениям.
Сначала необходимо определить входное комплексное сопротивление Zэ . Это можно сделать по исходной схеме рис. 3.14, а, но если это сложно, то можно перейти к упрощенной схеме, изображенной на рис. 3.14, б, введя следующие обозначения:
Z1 r1 j L1 r1 jxL1; |
|
||||||
Z2 |
r2 j L2 |
r2 |
jxL2; |
(3.84) |
|||
Z |
|
r j |
1 |
|
r jx . |
|
|
3 |
|
|
|||||
|
3 |
C |
3 |
C |
|
||
|
|
|
|
|
|
||
Получили в итоге последовательно-параллельное соединение трех комплексных сопротивлений, для которого
96

Zэ Z1
где zэ 
 rэ2 xэ2
rэ2 xэ2
э arctg xэ rэ
током i1.
Z2Z3 |
|
Z1 Z23 r1 jxL1 |
r2 jxL2 r3 jxC |
... |
||||||
Z |
2 |
Z |
3 |
r |
r |
j x |
x |
|
||
|
|
|
2 |
3 |
L2 |
C |
|
(3.85) |
||
rэ jxэ zэe j э ,
–полное (входное) сопротивление схемы;
–угол сдвига фаз между входным напряжением u и входным
Реактивное сопротивление xэ может быть как положительным (индуктивным), так и отрицательным (емкостным). Это зависит от соотношения параметров рассматриваемой схемы.
Комплексное действующее значение входного тока
I |
U |
|
Ue j |
I e j э I e j 1 . |
(3.86) |
|
|
|
|||||
1 |
Zэ |
|
zэe j э |
1 |
1 |
|
|
|
|
|
|
||
По комплексу тока I1 в случае необходимости записывается мгновенное значение тока:
i1 I1 |
|
sin t 1 . |
|
2 |
(3.87) |
Множитель 
 2 обозначает переход от действующего значения тока I1 к амплитудному значению I1m, поскольку в окончательном виде должно быть записано выражение:
2 обозначает переход от действующего значения тока I1 к амплитудному значению I1m, поскольку в окончательном виде должно быть записано выражение:
i1 I1m sin t 1 . |
(3.88) |
К значениям токов ветвей можно прийти различными путями, но наиболее общий путь характеризуется следующими этапами.
Выражаем напряжение U12 :
U |
IZ |
23 |
... U |
e j 12 . |
(3.89) |
12 |
|
12 |
|
|
Это напряжение приложено к обеим параллельным ветвям, поэтому
97

|
|
|
U12 |
... I2e j 2 ; |
|||
I |
2 |
||||||
Z2 |
|||||||
|
|
|
|
(3.90) |
|||
|
|
|
U12 |
|
|||
I |
|
|
|
... I e j 3 . |
|||
|
|
||||||
|
3 |
|
|
Z3 |
3 |
||
|
|
|
|
|
|||
По полученным значениям комплексов токов записываются мгновенные значения токов:
i |
I |
|
|
|
|
sin t |
|
; |
||
2 |
|
2 |
2 |
|||||||
|
2 |
|
|
|
|
|
|
(3.91) |
||
|
|
|
|
|
|
|
|
|
|
|
i |
I |
3 |
2 |
sin t |
3 |
. |
||||
|
3 |
|
|
|
|
|
|
|||
Впроцессе вычислений приходится применять преобразование комплексных чисел, так как для операции сложения и вычитания необходима алгебраическая форма комплексных чисел, а умножение и деление более удобно осуществлять, используя показательную (экспоненциальную) форму.
3.7.Виды мощности в электротехнике
Вобласти электрических цепей синусоидального тока используется несколько видов мощности: мгновенная, активная, реактивная, полная и мощность в комплексной форме, или комплексная мощность.
3.7.1. Мгновенная мощность
представляет собой произведение мгновенных значений напряжения и тока:
p u i. |
(3.92) |
Пусть u Um sin t , i Im sin t , т. е. ток отстает от напряжения на угол сдвига фаз φ. Подстановка этих значений в соотношение (3.92) дает следующее:
p u i Um sin t Im sin t UmIm sin t sin t . |
(3.93) |
|||
Произведение синусов преобразуется в соответствии с выражением |
|
|||
sin x sin y |
1 |
cos x y cos x y . |
(3.94) |
|
|
||||
2 |
|
|
|
|
98

Полагая x t , а y t
p |
1 |
U |
I |
cos |
|
||||
2 |
|
m |
m |
|
|
|
|
||
, приходим к результату:
cos 2 t |
UI cos cos 2 t . |
(3.95) |
|
|
|
|
|
Как видно из формулы (3.95), мгновенная мощность является периодической функцией, изменяющейся с двойной частотой по отношению к частоте напряжения и тока.
Рассмотрим сначала функцию мгновенной мощности для сопротивления r
(рис. 3.15, а).
Периодическая функция мгновенной мощности в этом случае не имеет отрицательных значений, ее среднее значение согласно выражению (3.95) равно произведению действующих значений напряжения и тока UI, поскольку 0 .
Мгновенная мощность пульсирует с двойной частотой, но нигде не меняет знака, что указывает на однонаправленность потока электрической энергии от источника к сопротивлению. Возврат энергии источнику отсутствует, поэтому в качестве главного свойства отмечается необратимость процесса преобра-
зования энергии в сопротивлении r. |
||
p |
p = u i |
|
u |
|
|
i |
|
|
UI |
|
|
|
i |
t |
|
|
|
|
u |
|
|
а |
|
p |
|
|
|
|
u |
u |
|
|
|
i |
|
i |
|
|
|
|
p = u i |
|
|
|
|
|
|
|
|
+ |
|
+ |
|
|
– |
– |
– |
t |
|
|
|
б |
|
Рис. 3.15. Мгновенная мощность:
а– сопротивление r; б – индуктивность L
Виндуктивности L угол сдвига фаз  2 , поэтому в уравнении (3.95) cos 0 и кривая мгновенной мощности симметрична относительно оси вре-
2 , поэтому в уравнении (3.95) cos 0 и кривая мгновенной мощности симметрична относительно оси вре-
мени (рис. 3.15, б). Это значит, что в части периода энергия поступает от источника в индуктивность, в другой – возвращается источнику. На участках графика, отмеченных знаком «плюс», энергия магнитного поля индуктивности
99
