
- •1. Матрицы и действия над ними.
- •2. Определители второго и третьего порядков.
- •3. Миноры и алгебраические дополнения.
- •4. Обратная матрица.
- •5. Решение систем линейных алгебр. Уравнений. Теорема Крамера.
- •6. Линейная балансовая модель Леонтьева.
- •7. Метод Гаусса-Жордана.
- •8. Ранг матрицы. Теорема Кронекера-Капелли.
- •9. Прямоугольная система координат в пространстве. Понятие вектор. Проекция вектора на ось. Направляющие косинусы вектора.
- •10. Линейные операции над векторами. Теоремы о проекциях векторов. Линейная зависимость векторов.
- •11. Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
- •12. Векторное произведение. Выражение векторного произведения через координаты векторов.
- •13. Смешанное произведение трех векторов. Выражение смешанного произведения через координаты векторов.
- •14. Векторное параметрическое уравнение прямой. Задача о делении отрезка в зад. Отношении.
- •1 5. Координатные уравнения прямой в пространстве.
- •16. Координатные уравнения прямой на плоскости.
- •17. Угол между двумя прямыми. Взаимное расположение прямых на плоскости.
- •18. Координатные уравнения плоскости.
- •19. Общие уравнения прямой в пространстве.
- •2 0. Взаимное расположение прямых и плоскостей в пространстве
- •22. Поверхность второго порядка
- •1. Множества. Грани числовых множеств. Абсолютная величина числа. Понятие функции. Классификация функций.
- •2.Предел последовательности. Понятие сходящейся последовательности. Теоремы о сходящихся последовательностях (единственный предел, необходимое условие сходимости)
- •4.Первый замечательный предел.
- •5.Второй замечательный предел.
- •6.Бесконечно-большие и бесконечно‑ малые функции. Сравнение бесконечно‑малых функций. Асимптотические формулы.
- •7.Непрерывность функции в точке. Классификация точек разрыва.
- •8.Основные теоремы о непрерывных функциях.
- •9.Понятия сложной и обратной функций.
- •10. Понятие производной. Геометрический и физический смыслы производной.
- •11. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности.
- •12. Правила дифференцирования суммы, разности, произведения и частного.
- •13. Понятие дифференциала. Дифференциал суммы, разности, произведения и частного.
- •14. Производные постоянной, тригонометрических и логарифмической функций.
- •15. Производные обратной и сложной функций
- •16. Производные показательной и обратных тригонометрических функций.
- •17. Логарифмическая производная. Производная степенной функции.
- •18. Таблица производных простейших элементарных функций.
- •19. Дифференцирование функции, заданной параметрически.
- •20. Теоремы Ферма и Ролля.
- •21. Теорема Лагранжа и Коши.
- •22. Теорема Лопиталя.
- •23. Теорема Тейлора.
- •24. Признак монотонности.
- •25. Направление выпуклости.
- •26. Необходимые условия точки перегиба.
- •27. Асимптоты графика функции.
- •28. Комплексные числа.
- •29. Тригонометрическая форма комплексного числа.
- •30. Возведение комплексного числа в степень и извлечение корня.
2.Предел последовательности. Понятие сходящейся последовательности. Теоремы о сходящихся последовательностях (единственный предел, необходимое условие сходимости)
Если
по некоторому закону каждому натуральному
числу n поставлено в соответствие вполне
определенное число
 ,
то говорят, что задана числовая
последовательность
,
то говорят, что задана числовая
последовательность

Для
любого
 существует номер, зависящий от эпсилонта,
такой, что для всех членов последовательности
с номерами больше, чем этот номер
выполняется неравенство
существует номер, зависящий от эпсилонта,
такой, что для всех членов последовательности
с номерами больше, чем этот номер
выполняется неравенство
 ,
,
 .
.

Последовательность, имеющая предел называется сходящейся, при этом все арифметические действия производятся только со сходящимися последовательностями.
Теорема1: сходящиеся последовательности имеют единственный предел)
Док-во:
Пусть
 имеет предел b≠a,
имеет предел b≠a,

окрестности
не имеют общих точек, тогда по определению
предела в эпсилон окрестности точки А
содержится бесконечно много членов
последовательности
 ,
а вне этой окрестности конечное число
членов, тогда точка В не может быть
пределом последовательности.
,
а вне этой окрестности конечное число
членов, тогда точка В не может быть
пределом последовательности.
Теорема 2: сходящаяся последовательность ограничена.
Док-во:
Из определения последовательности,
можно записать
 ,
,
 .
Так как модуль суммы не превосходит
суммы модулей, то
.
Так как модуль суммы не превосходит
суммы модулей, то
 ,
тогда
,
тогда

Положим
 ,
,
 ,
т.е. последов-ность
ограничена.
,
т.е. последов-ность
ограничена.
3.Бесконечно-большие и бесконечно-малые последовательности. Теоремы о сумме (разности), произведении и частном двух сходящихся последовательностях. Предельный переход в неравенствах. Монотонные последовательности. Число ℮. Предел функции. Теоремы о пределах функции.
Последовательность
справедливо
|
Последовательность называется бесконечно малой, если справедливо
|
Теорема
1:
Если
бесконечно большая, то
 является
бесконечно малой и наоборот, если
бесконечно малая, то
бесконечно
большая.
является
бесконечно малой и наоборот, если
бесконечно малая, то
бесконечно
большая.
Док-во:
Пусть
бесконечно большая,
т.е.
и
.
 ,
тогда
,
,
тогда
,
 ,
,
,
,
 .
.

 -
бесконечно большая;
-
бесконечно большая;
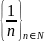
 - бесконечно малая.
- бесконечно малая.
Теорема
2:
Если последовательность
 и
и
 бесконечно малые, то
бесконечно малые, то
 ,
бесконечно малая (
,
бесконечно малая ( ).
).
Док-во:

 ;
;
 ,
,
 ;
;

 -
бесконечно
малая.
-
бесконечно
малая.
Теорема
3:
Произведение двух бесконечно малых
последовательностей есть последовательность
бесконечно малая. ( )
Док-во:
)
Док-во:
 ;
;

 ,
,
 ,
,
 – бесконечно
малая последовательность.
– бесконечно
малая последовательность.
Теорема
4:
Произведение ограниченной последовательности
на бесконечно малую есть последовательность
бесконечно малая. (
Док-во:
– ограниченная;
,

– бесконечно
малая;
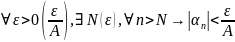
;
 ,
,
 – бесконечно
малая послед-ость.
– бесконечно
малая послед-ость.
Следствие:
Если
имеет предел равный А, то это означает,
что
 -бесконечно малая последовательность.
-бесконечно малая последовательность.
Справедливо и обратное: Если -бесконечно малая последовательность, то имеет предел равный А.
Теорема
о сумме (разности):
Сумма (разность) двух сходящихся
последовательностей есть последовательность
сходящаяся, предел которой равен сумме
(разносте) пределов этих последовательностей.
( )
)
Док-во:
 - бесконечно малая ;
- бесконечно малая ;
 - бесконечно малая
- бесконечно малая
 ;
;
 ,
тогда
,
тогда
 и
и

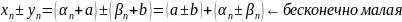

.
Теорема
о произведении:
Произведение двух сходящихся
последовательностей есть последовательность
сходящаяся, предел которой равен
произведению пределов этих
последовательностей. 0
Док-во:
и
0
Док-во:
и


 – бесконечно
малая, тогда
– бесконечно
малая, тогда
 .
.
Теорема
о частном:
частное двух сходящихся последовательностей
есть последовательность сходящаяся,
предел которой равен частному пределов
этих последовательностей.
 Док-во:
аналогично двум предыдущим!
Док-во:
аналогично двум предыдущим!
Предельный переход к неравенствам:
Теорема
1: Если все члены последовательности
удолетворяют неравенству
 ,
то предел последовательности a ≥b.
,
то предел последовательности a ≥b.
Теорема
2 (теорема о двух полицейских – о сжатой
переменной): Если последовательности
,
и
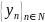 ,
и
,
и
 удовлетворяют
удовлетворяют
 .
.
Монотонные последовательности:
1. 2. |
3. 4. |
!Монотонная ограниченная последовательность сходится.
Число
e:
 (неперовое
число)
(неперовое
число)
 ,
,
 ;
;
 ;
…;
;
…; ;….
;….
 .
.
Предел f(x) определена в некоторой окрестности точки, за исключением только если самой точки.
1.По
Гейне:
Число А называется пределом функции
f(x)
при
 ,
если для любой последовательности
сходящийся к
,
если для любой последовательности
сходящийся к
 ,
последовательность значений функции
,
последовательность значений функции
 сходится к А. (
сходится к А. (
2.По
Каши:
Число А называется пределом функции
 .
.
Односторонним
предел: Число А называется пределом
функции f(x) справа при
 ,
если
,
если
 ,
такое что
,
такое что
 ,
то
,
то
 .(
.( :
Число А называется пределом функции
f(x) слева при
:
Число А называется пределом функции
f(x) слева при
 ,
если
,
такое что
,
если
,
такое что
 ,
то
.
(
,
то
.
( )
)
Предел
функции при
 :
:
Число
А называется пределом функции (x) при
,
если
 .
.
Теоремы о пределах функции:
Теорема
1: Если f(x), g(x) при
имеют предел А и В, то
 соответственно имеют пределы А±В,
соответственно имеют пределы А±В,
 .
.
Теорема
2 (о сжатой переменной): Если функции
f(x)
и
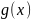 ,
и
,
и
 удовлетворяют
удовлетворяют
 .
.

 наз. бесконечно большой, если
наз. бесконечно большой, если

 .
.

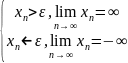
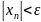 .
.
 послед-ость
возврстающая
послед-ость
возврстающая послед-ость
неубывающая
послед-ость
неубывающая послед-ость
убывающая
послед-ость
убывающая послед-ость
невозврста-ая
послед-ость
невозврста-ая