Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный институт электроники и математики (технический университет)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ОТВЕТНИК ВСЕ В ОДНОМ. ФОРМАТ А5

.pdf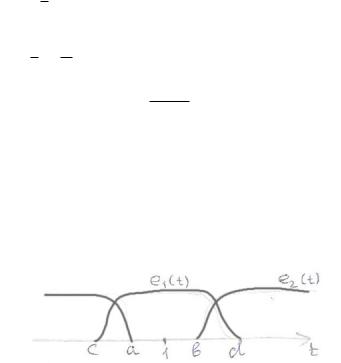

Скачиваний:

Добавлен:

08.02.2015

Размер:

981.9 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Задача 3.2.

Найти главный член асимптотического разложения интеграла

exp i

dx;

! +1:

Решение.

Сделаем замену: s = p3

, x = 31 t = s 1t

dx = s 1dt

1 t2

= 3 t 1 +

3 t2 = 3 t 1 +

3 t2

= s

таким образом исходный интеграл перепишется в виде:

1 Z +1

s 0

f(t) = 1 + t2 t 2


1			t2		1
exp is		+		dt =			F1	(s)
	t		2			s
f0(t) = t 2 + t = 0;					f00(t) = 2t 3 + 1

f0(t) = 0	)		t3 1	= 0	)	t = 1
f0(t) = 0			t2	= 0		t = 1
			t2
	f00(1) = 2 + 1 = 3
		f(1) =		3
		f(1) =		2
				2

t = 1 - стационарная точка функции f(t)

Вариант решения 1.

Ðèñ. 1:

e1(t) + e2(t) = 1

e1(t)eisf(t)dt + Z0

eisf(t)dt = Z 1

e2(t)eisf(t)dt + Zb

1 e2(t)eisf(t)dt

{zI3

} |

{zI1

} |

{zI2

}

I1 è I2 - интегралы по интервалам, не содержащим стационарную точку функции f(t), следовательно интегрированием по частям можно показать, что:

1 1

I1 = O SN ; I2 = O SN ; 8N > 0

+1	e1eisf(t)dt = Zc	d
I3 = Z 1	e1eisf(t)dt = Zc	eisf(t)dt

ê I3 åñëè

применим формулу метода стационарной фазы:

F ( ) = Rab ei f(x) (x)dx, òî

F ( ) =

1 ei f(x0)+i 4 signf00

(x0)

f00

(x0)

(x0) + O

j j

ãäå x0 - стационарная точка функции f(x). Таким образом:

1s eis 2

+i 4

+ O

s !

j j

F1(s) = s jsjei 2 s+i

+ O

Вариант решения

exp is

dt =

'(t) exp is

dt = F~(s);

ãäå

(

'(t) = 1; t > 0; 0; t < 0:

Применим формулу метода стационарной фазы: если F ( ) = Rab ei f(x) (x)dx, òî

F ( ) =

1 ei f(x0)+i 4 signf00(x0)

f00(x0)

(x0) + O

1S e2 is+ 4 i

F~(s) =

'(1)

+ O

j j

3 !

3 3

2 i

4 i

F ( ) =

1 F (

) =

Ответ:

	2		+i	r	3		3
	1 i 3 3		+i		2		1
1
F ( ) =	1	e 2	4			+ O	1

Задача 4.1.

Найти решение задачи:

u = uxx; t > 0; 0 < x < l
8utt=0 = u0 = Const
> j
>
>
<
u	x=0 = u1 = Const
>>ujxxj=l = 0
>
:

Решение.

решение задачи будем искать в виде

u = U(x; t) + v(x; t)

где U такое что

8Ux x=0			= u1
>	U(x; t) = a(t)x + b(t)
	j
<U x=l = 0
>	j		a(t) = u	1
:
		u1l + b = 0
			b = u1l
	U(x; t) = u1x u1l
u = u1x u1l + v(x; t)
ut = vt		ux = u1 + vx uxx = vxx

исходная задача перепишется в виде:

>vt = vxx

<vxjx=0 = 0

>>vjx=l = 0

:vjt=0 = u0 u1x + u1l

рассмотрим задачу

(

vt = vxx

vxjx=0 = vjx=l = 0

решение этой задачи будем искать в виде

v(x; t) = X(x)T (t)

XT 0		= X00T
X00			T	0	=
	=
X			T

X00 + X = 0

T 0 + T = 0

X0(0) = X(l) = 0

(

X00 + X = 0

X0(0) = X(l) = 0

ищем нетривиальное решение задачи

1) < 0

2 + = 0

X = C1e x + C2e x

X0 = p

C1e x p

C2e x

) C1 = C2

(0) =

C1 C2 = 0

X(l) = C1(e l + e l) = 0 ) C1 = 0

X(x) 0 (не подходит)

2) = 0

X = C1 + C2x

X0(0) = C2 = 0

X(l) = C1 = 0

X(x) 0 (не подходит)

3) > 0

= i

X = C1 cos p

x + C2 sin p

X0 = C1 sin x +

C2 cos x

) C2 = 0

C2 = 0

C1 cos p

l = 0

l =

+ n ;

n = 0; 1; :::

(

+ n)

( n

= l22

(21

+ n)2;

n = 0; 1; :::

= cos (1 + n)x

разложим функции из начальных и граничных условий по

kXnk2 =	0	l	cos2			(	1	+ n)x dx =	0	l 1 + cos	2 (1		+ n)x
kXnk2 =	0		cos2		l	(	2	+ n)x dx =	0		l2	2
	Z								Z
1				(	1	+ n)x ;
x = n=0 n cos l				(	2	+ n)x ;
X

dx = 2l

n 6= k

+ n)x cos

+ k)x dx = 0

cos

+ n)x dx = n Z0

+ n)x dx

= x cos

cos2

n = l Z0

l (2

+ n)x dx =

x cos

+ n)x dx;

= fu = x; du = dx; dv = cos l

)x g =

v =

sin

(n +

(n + 21 )

= l (n + 21 ) sin

(

2 + n)x j0l (n +

(

2 + n)x dx =

21 ) Z0

sin l

sin h

+ n i +

cos

(

+ n)x j0l =

(n + 21 )

2(n + 21 )2

( 1)nl2

(

1)n

2(n + 21 )

(n + 21 )

таким образом

21 ) ( 1)n

+ n)x

x = n=0

(n +

(n + 21 ) cos l (2

C =

n cos

(

+ n)x;

C = Const

n=0

cos

(2 + n)x dx = n cos2 l (

2 + n)x dx

C Z0

l 2

l (2

+ n)

l 2

n =

cos

(

+ n)x dx =

sin

(

+ n)x

l =

(

1)n =

( 1)n2C

(21 + n)

C =

( 1)n2C

cos

(

+ n)x

n=0

(21 + n)

l 2

таким образом

u0 + u1l u1x =

( 1)n2(u0 + u1l)

2u1l( 1)n

2u1l

cos

(

+ n)x =

n=0

(21 + n)

( (21 + n))2 l 2

( 1)n2u0

2u1l

cos

(

+ n)x

n=0

( (21 + n))2

(21 + n)

l 2

v(x; t) =

gn(t)Xn(x)

n=0

(

1 g 0X =

1 g X 00 =

1 g X

n=0 gn(0)Xn =

n=0

(

+n)

(n+ 2 )

n=0 n n

n=0

n n n

1 ( 1)

2u0

2u1l

gn0 =

(21 + n) 2 gn

(gn(0) =

( 1

+n)

2(n+ 1 )2

2u0

2u1l

( 1)

gnn

= l (

2 + n)

ln gn = l (2 + n)

t + C1

gn(t) = C2e ( l ( 21 +n))2t

gn(0) = C2

( 1)n2u0

2u1l

2(n +

1 )2

(

+ n)

gn(t) =

( 1)n2u0

2u1l

e ( l ( 21 +n))2t

(21 + n)

2(n + 21 )2

(21

( 1)nu0 +

u1l

t cos

v(x; t) = n=0

+ n)

(n + 21 ) e ( l

( 2 +n))

l (12 + n)x

Ответ:

(

( 1)nu0 +

u1l

u(x; t) = n=0

(21 + n)

(n + 21 )

e ( l (

+n))

2 + n)x ) + u1x u1l

cos l (

Задача 4.2.

Доказать что в R3 любая !2 может быть представлена в виде

!2 = P x2 ^ x3 + Qx3 ^ x1 + Rx1 ^ x2

Решение: e1 = (1; 0; 0) e2 = (0; 1; 0)

e3 = (0; 0; 1)

1 2 R3, 2 2 R3

x1, x2, x3 - линейная система координат в R3

1 = x1( 1)e1 + x2( 1)e2 + x3( 1)e3

2 = x1( 2)e1 + x2( 2)e2 + x3( 2)e3

!2( 1; 2) = { используется свойство линейности 2-форм по обоим аргументам } =

=x1( 1)!2(e1; 2) + x2( 1)!2(e2; 2) + x3( 1)!2(e3; 2) =

=x1( 1)x1( 2) !2(e1; e1) +x1( 1)x2( 2)!2(e1; e2)+x1( 1)x3( 2)!2(e1; e3)+

|{z }

x2( 1)x1( 2)!2(e2; e1) + x2( 1)x2( 2) !(e2; e2) +x2( 1)x3( 2)!2(e2; e3)+

| {z }

x3( 1)x1( 2)!2(e3; e1) + x3( 1)x2( 2)!2(e3; e2) + x3( 1)x3( 2) !2(e3; e3) =

{ используем !2( ; ) = 0 è !2( ; ) =

2 !2( ; )} =

}

! (e1; e2)(x1( 1)x2(2 2) x1( 2)x2( 1)) + ! (e2; e3)(x2( 1)x3( 2)

x2( 2)x3( 1)) + ! (e3; e1)(x3( 1)x1( 2) x3( 2)x1( 1)) =

( 2) x2

( 2)

!2(e1; e2) +

( 2) x3

( 2) !2(e2; e3)+

( 1) x2

( 1)

( 1) x3

( 1)


+		x3( 1) x1( 1)									!2(e3; e1) =
=	!2(3e			;2e )(x			1		x )(				; ) + !2	(e	; e )(x	2		x	)(	;	)+
		1		2			1			2	1		2	2	3	2		3	1	2
+!		x ( )			x1			( 2)		)(
+!		2(e	; e )(x			3			^x	)(		; )					^
		3		1		3		^		1	1		2

следовательно

!2 = !2(e1; e2)(x1 ^ x2) + !2(e2; e3)(x2 ^ x3) + !2(e3; e1)(x3 ^ x1)

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.08.2019210.94 Кб4ОС_лаб_dos.doc
#
29.08.2019505.86 Кб2ОС_лаб_nc.doc
#
29.08.20191.14 Mб2ОС_лаб_wc.doc
#
08.02.20151.3 Mб122Основы Дискретной математики.pdf
#
08.02.2015875.01 Кб85ответник 10-11.doc
#
08.02.2015981.9 Кб13ОТВЕТНИК ВСЕ В ОДНОМ. ФОРМАТ А5.pdf
#
08.02.20152.62 Mб63Ответник к госэкзамену_Белов.docx
#
08.02.20151.89 Mб120Ответник на госы.docx
#
08.02.20154.3 Mб26ответник по БЖД.doc
#
28.04.20199.45 Mб11Ответник.doc
#
06.08.2019476.93 Кб4Ответы Информатика.docx