
2514
.pdfКонстанты , и b определяются из экспериментальных данных:
= 0 при кручении, = |
|
при растяжении, = |
|
при сжатии. |
|
|
|||
6 |
6 |
|
||
Энергетический вариант теории ползучести позволяет определять долговечность деталей ДВС с учетом истории нагружения, учитывающей любые изменения температурно-силового диапазона, и совпадает с теорией длительной прочности. Под длительной прочностью понимают время в часах, в течение которого материал выдерживает нагрузку при заданных температуре и напряжениях. Например, сталь 40Х10С2М при 550 С выдерживает нагрузку дл = 24кг/мм2 в тече-
ние 100 ч (табл. П.10).
Лекция 3. Численные методы исследования напряженнодеформированного состояния деталей ДВС. Метод конечных элементов
Описание физико-химических процессов, протекающих в двигателе внутреннего сгорания и его элементах, базируется на основных законах сохранения массы, энергии и количества движения, описываемых системами дифференциальных уравнений в частных производных. Моделирование может вестись по временной и по пространственной переменным. Решить поставленную задачу позволяет применение численных методов с использованием современных ЭВМ.
К наиболее распространенным способам численного решения систем дифференциальных уравнений ДВС относятся метод конечных разностей (МКР) и метод конечных элементов (МКЭ). В последнее время начинает применяться еще метод граничных элементов (МГЭ). Рассмотрим только основные идеи этих методов, и затем каждый из вас в процессе выполнения курсового проекта попробует сделать расчет напряженно-деформированного и теплового состояния цилиндропоршневой группы.
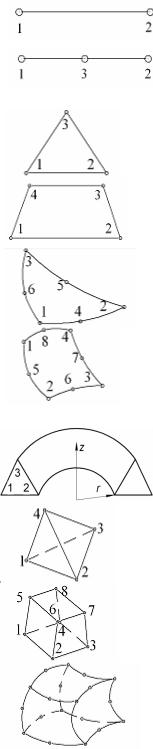
В основе МКЭ лежит дискретизация расчетной области с целью определения напряженно-деформированного состояния в любой точке области на основе решения систем уравнений механики сплошной среды. При этом основные этапы метода конечных элементов состоят
вследующем:
1.Рассматриваемая область разбивается на конечное число подобластей – конечных элементов. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют всю форму области. Векторы внешних нагрузок прикладываются к узлам на границе области.
30
|
|
|
|
|
|
Таблица 3.1 |
|
|
|
|
|
Функции формы |
|||
Название конечного элемента |
|
Число |
Функции формы Ni конечно- |
|
|||
|
узловых |
го элемента в естественных |
|
||||
|
|
|
|
|
точек |
координатах |
|
Стержневые: |
|
|
|
|
|||
симплекс- |
|
|
2 |
y(x)=a1+a2x |
|
||
элемент |
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
квадратичный |
|
|
3 |
y(x)=a1+a2x+a3x2 |
|
||
элемент |
|
|
|
|
|
||
Плоские элементы: |
|
|
|
|
|||
треугольный |
|
|
|
|
|
||
элемент |
|
|
3 |
u(x) = a0 + a1x + a2y |
|
||
|
|
|
|
|
|
|
|
четырехуголь- |
|
|
|
|
|
||
ный элемент |
|
|
4 |
u(x) = a0 + a1x + a2y + a3xy |
|
||
|
|
|
|
|
|
|
|
треугольный |
|
|
|
u(x) = a0 + a1x + a2y + a3x2 + |
|
||
изопараметри- |
|
|
6 |
|
|||
ческий элемент |
|
|
+ a4y2 + a5xy |
|
|||
|
|
|
|
|
|
|
|
четырехугольный |
|
|
|
u(x) = a0 + a1x + a2y + a3xy + |
|
||
изопараметриче- |
|
|
8 |
|
|||
ский элемент |
|
|
a4x2 + a5y2 + a6xy2 + a7x2y. |
|
|||
|
|
|
|
|
|
||
Объемные или трехмерные элементы: |
|
|
|||||
осесимметрич- |
|
|
|
|
|
||
ный элемент |
|
|
3 |
u(x)=a0+a1r+ a2z |
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
тетраэдальный |
|
|
|
|
|
||
элемент |
|
|
4 |
u(x) = a0 + a1x + a2y + a3z |
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
призматический |
|
|
|
u(x) = a0 + a1x + a2y + a3z+ |
|
||
шестигранный |
|
|
8 |
|
|||
элемент |
|
|
|
|
+a4xy+ a5yz+ a6zx+ a7xyz |
|
|
|
|
|
|
||||
|
|
|
|
|
|
||
изопараметри- |
|
|
|
|
|
||
ческий шести- |
|
|
20 |
|
|
||
гранный эле- |
|
|
|
|
|||
мент |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
2.Исследуемая непрерывная функция в каждой узловой точке считается неизвестной, подлежащей дальнейшему определению.
3.Непрерывная величина функции аппроксимируется на каждом элементе с помощью выбора определенного набора функций, вид которых зависит от типа элемента и количества узловых точек, входящих в него. Полиномы подбираются таким образом, чтобы непрерывность функции сохранялась вдоль границы элемента.
Представленные уравнения конечных элементов называются функциями формы (табл. 3.1). Они значительно упрощаются, если ввести локальную систему координат с пределами изменения пере-
менной 1 1. Тогда поле перемещений = [u, v, w] в изопараметрических конечных элементах задается через функции формы элемента, которые собираются в матрицу [N], т.е. =N{ }, где { ij} – узловые перемещения.
Понятие о матрице жесткости
Рассмотрим консольную балку, нагруженную силой F1 на конце.
Вертикальные перемещения точки приложенной силы равно y Fl3 , 3EJ
где Е – модуль упругости; J – момент инерции поперечного сечения |
|||||
балки. Если перемещение y задано, то сила F 3EJ |
y или F= Ky, где |
||||
|
|
К 3EJ |
l3 |
|
|
|
|
и у F . |
|
(3.1) |
|
|
|
l3 |
K |
|
|
Величина K называется коэффициентом жесткости. K – есть си- |
|||||
ла, которую надо приложить на конце балки, чтобы прогиб был равен |
|||||
l |
|
единице. Пусть на балку действует еще вто- |
|||
|
|
рая сила F2, тогда |
|
|
|
|
F |
y1= 11F1+ 12F2; y2= 21F1+ 23F2, |
(3.2) |
||
|
11 |
где 11 – перемещение в направлении y1 под |
|||
|
y |
действием единичной силы, направленной |
|||
|
по F1, величины ij называют коэффициен- |
||||
|
|
||||
F |
F |
тами влияния и они зависят от геометриче- |
|||
11 |
ских характеристик балки и от модуля уп- |
||||
22 |
|
||||
|
1 |
ругости. |
|
|
|
|
Поле |
перемещений |
равно в |
общем |
|
2 |
y |
||||
y |
|
случае |
Y= F. |
|
(3.3) |
|
|
|
|||
|
|
32 |
|
|
|
Тогда в матричной форме: F |
F |
; Y |
y |
, а |
|
11 |
|
|
||
1 |
y |
1 |
|
|
12 |
– |
||||
|
F |
|
2 |
|
|
21 |
22 |
|
||
|
2 |
|
|
|
|
|
||||
матрица податливости. Заметим, что матрица податливости симметрична, так как 21 = 12 по теореме Максвелла о взаимности перемещений.
Если перемещения известны, то из F = -1Y можно найти силы, но F = K Y, тогда K= -1, т.е матрица жесткости будет равна обратной матрице податливости. Переходя к объемным конечным элементам, имеем:
Вектор нагрузок Fe Fie,Fie , где Fie,Fie – матрицы сил уз-
лов i, j, ..., причем Fie,Fie – поверхностные силы и эквивалентные поверхностным напряжениям узловые силы, а также объемные силы.
Ve = ie, ej ,... – вектор приращений перемещений от нагрузок.
Силы Fie,Fie будем считать эквивалентными действующим нагрузкам т.е. KVe=Fe, где матрица жесткости имеет вид
|
|
|
|
e |
e |
1 |
|
|
|
|
|
ij |
ij .... |
|
|
|
e |
|
e |
e |
|
|
|
K |
|
|
|
. |
|||
|
ji |
ji |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В основу МКЭ положен вариационный принцип Лагранжа, в соответствии с которым равновесное состояние, в которое может перейти твердое тело под действием приложенных сил, характеризуется минимумом потенциальной энергии.
Полная потенциальная энергия всей системы равна деформации тела Э и работы массовых и поверхностных сил.
Для установившегося состояния можно записать
Э 0,5 |
|
(3.4) |
dx, |
где - матрица относительных деформаций; – матрица напряжений; x – матрица рассматриваемой области твердого тела; – вся рассматриваемая область тела.
Деформации у можно выразить через перемещения с помощью уравнений Коши
33
|
|
|
|
|
|
|
|
|
V |
|
|
Vj |
|
|
|
|
|
|
||||||
|
|
|
|
ij |
0,5 |
|
|
|
i |
|
|
|
|
|
, |
|
|
|
|
(3.5) |
||||
|
x |
|
|
x |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
||
где Vi– перемещение по оси Хi или в матричной форме |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
=0,5[D][V], |
|
|
|
|
|
(3.6) |
|||||||||||
где D – оператор дифференцирования уравнений Коши; [V] - матрица |
||||||||||||||||||||||||
перемещений точек тела. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
D |
|
|
|
z |
. |
|
|
|
|
|
(3.7) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y |
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Деформация и напряжения связаны между собой с помощью мат- |
||||||||||||||||||||||||
рицы Е, характеризующей упругие свойства среды: |
|
|||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
=[E][ ] , |
|
|
|
|
(3.8) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
0 |
0 |
0 |
|
|
|
||||||||||
E |
|
|
|
|
|
|
|
|
|
|
|
2 0 |
0 |
0 |
|
, |
(3.9) |
|||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
0 |
0 |
|
|
|
||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
||||
, – множители Ляме.
|
Ev |
; |
E |
. |
(3.10) |
(1 v)(1 2v) |
|
||||
|
|
2(1 v) |
|
||
E – модуль упругости тела; – коэффициент Пуансона, при этом модуль сдвига G=0,5 E/(1+ ).
34

dV dxdydz J d d d , J – определитель матрицы Якоби.
Если якобиан равен 0, то элемент вырожденный, необходимо повторить разбиение на элементы, чтобы не было нулевых.
Подставляя (3.8) и (3.6) в (3.4), получаем
Э 0,5 |
|
|
|
T |
|
E |
|
|
D |
|
dx |
(3.11) |
|
D V |
|
|
V |
|
|
Или можно записать
Э 0,5 T 0 dV 0,5 P T 0 dS,
V S
где - объемные силы; Р – внешние поверхностные силы; – деформации от ; р – деформации от поверхностных сил Р.
Решение задачи дает поле перемещений V(x). Это решение аппроксимируется с помощью координатных функций формы N и неопределенных коэффициентов Q.
Матрица перемещений U(x)=[N][Q]. (3.12) Заменяя в (3.6) V(x) на U(x), получим
Э 0,5 QT DN T EDNdx 0,5QT KQ, |
(3.13) |
V |
|
где K DN T EDNdx – матрица жесткости. |
|
V V V |
|
Дифференцируя (3.4) находим |
|
KQ=B, |
(3.14) |
где B – вектор нагрузок и задача анализа прочности в МКЭ све-
Q
лась к решению системы линейных алгебраических уравнений (3.5).
Задачу определения вектора Q неопределенных коэффициентов системы решают или методом коллокаций, или методом наименьших квадратов, или методом Галеркина, с помощью которых минимизируются невязки в среднем по области интегрирования. При этом после замены функции перемещения V(x) аппроксимирующим выражением N(x)Q в исходном дифференциальном уравнении Ляме
( G)graddivV(x) G V(x) R(x) 0,
где – дифференциальный оператор |
( |
2 |
|
2 |
|
2 |
), применяемый |
|
x2 |
x2 |
x2 |
||||||
|
|
|
|
|
||||
|
1 |
2 |
|
3 |
|
|||
35 |
|
|
|
|
|
|
|
|
по всем элементам вектора V(x); R(x) – вектор массовых и приложенных сил. Матрица жесткости обычно сильно разрежена, поэтому для решения (3.5) применяют методы решения разреженных матриц (метод Гаусса, метод Халецкого и др.).
Применение МКЭ сводится к следующим операциям:
1.Создание геометрической модели исследуемой среды (детали) путем геометрического моделирования или вручную на экране дисплея.
2.Выбор из библиотеки модели КЭ, задание внешних нагрузок и значений геометрических и физических параметров и граничных условий.
3.Создание в геометрической модели сетки конечных элементов
сопределением координат условных точек.
4.Приведение имеющихся объемных сил и поверхностных нагрузок к узлам сети.
4 |
|
|
13 |
|
18 |
|
|
171 |
3 |
10 |
109 |
15 |
207 |
19 |
20 |
1 |
12 |
17 |
|||||
181 |
310 |
316 |
319 |
325 |
328 |
334 |
235 |
2 |
|
|
11 |
|
16 |
|
|
299 |
|
|
291 |
|
263 |
|
|
а
> 350 C
б
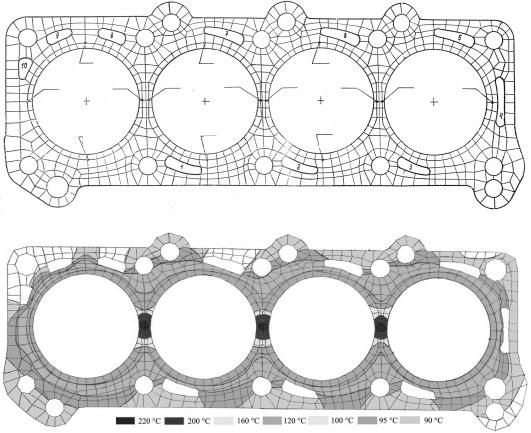
Рис. 3.1. Конечно-элементное разбиение (сетка) блока цилиндров одного из двигателей фирмы «Москвич»: а) в числителе обозначены номера термопар, фиксировавших температуру во время испытаний двигателя, в знаменателе приведены значения замеренных температур; б) температурные поля блока цилиндров
36

5.Объединение всех конечных элементов в единую конечноэлементную модель детали. При объединении элементы матрицы K образуются суммированием тех элементов матриц жесткости Ki, отдельных КЭ, которые относятся к одному и тому же узлу и направлению перемещения.
6.Решение системы уравнений (3.14).
7.Представление результатов решения либо в виде деформированной детали, либо распределения интенсивности напряжений или температур в виде гаммы цветовой окраски.
Лекция 4. Метод конечных разностей. Метод граничных элементов
Для приближенного решения задач теплопроводности и некоторых задач газовой динамики широко применяется метод конечных разностей (метод сеток). В нем область непрерывного изменения функциональной зависимости заменяется расчетной сеткой – дискретным множеством точек (узлов).
Частные производные, входящие в дифференциальные уравнения и граничные условия, заменяются разностными соотношениями. В результате такой замены решение задачи в частных производных сводится к решению системы разностных алгебраических уравнений. Несмотря на то, что число неизвестных в этой системе значительно, решение ее упрощается, а с применением ЭВМ не вызывает проблем.
Пусть температура тела изменяется от a = 100 °C до b=500 °C. При равномерном разбиении интервала имеем: xi = a+ih, где
i = 0, 1,..., N+1, а h b a .
N 1
Пусть некоторая функция f(x) = u является аналитической, разложим ее в ряд Тейлора в окрестностях точки xi.
|
|
h2 |
|
|
|
|
|
u |
, |
||
u(x h) u(xi) hu (xi) |
2! |
(xi) |
|||
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
||
|
|
|
|
||
u(x h) u(xi) hu (xi) |
2! |
u (xi). |
|||
|
|
|
|
|
|
Сложив оба выражения, получим изменение функции в узле i.
1
u (xi) h2 u(xi h) 2u(xi) u(xi h) ,
37
а если вычтем, то получим с точностью до более высокого порядка
малости: |
u (xi ) |
1 |
u(x h) u(x h) . |
|
2h |
||||
Для одномерной задачи имеем: |
xk =khkh |
|||
|
|
h |
h |
|
|
|
k |
||
xk+1/2+1/2==xkx+0k +,5h0,5h
0 |
1 |
2 |
k--11 |
k |
k+11 |
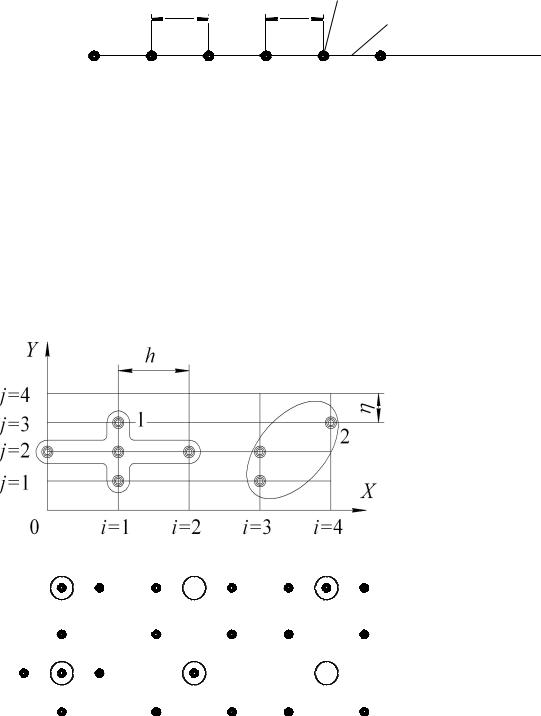
Рис.4.1. МКР для одномерной задачи
Для двумерной величины получаем сетку на плоскости: с шагом h по оси х и по оси y.
В точках задаются граничные условия: u(x=k=0)=a; u(x=k=N+1)=b
или значения u0 и uN+1 определяются из граничных условий.
При использовании метода МКР нужно выбирать правильно шаг сетки и вид шаблона. Под шаблоном понимают множество узловых точек, значения в которых используются для аппроксимации производной в одной конкретной точке.
|
|
|
-1 |
|
1 |
-1 |
|
1 |
|
1 |
-2 |
1 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
1 |
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
-1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.2. Шаблоны МКР для двумерных задач
38
Примеры шаблонов для одномерных
идвумерных задач приведены на рис. 4.1
и4.2. Кружком большего диаметра обозначены узлы, в которых аппроксимируется производная. Черными точками обозначены узлы, значения переменной в которых входят в вычисление искомой производной. Числа около узла – это коэффициент, с которым значение пере-
менной узла входит в шаблон вычисления. Для одномерных шабло- |
||||||||
нов (см. рис. 4.1) показана аппроксимация производных |
u |
|
|
|||||
|
|
|
||||||
x |
u |
(x) в |
||||||
точке К. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
На рис. 4.2 показаны шаблоны для двумерных задач: |
|
|||||||
h2 2U h2(U1 U2) Uk i, j Uk i, j Uk, j 1 Uk, j 1 4Uk, j ; |
|
|||||||
2h2 2U Uk i, j 1 Uk i, j 1 Uk 1, j 1 Uk 1, j 1 4Uk, j ; |
|
|
|
|||||
4h2Ux1x2 Uk i, j 1 Uk i, j 1 Uk 1, j 1 Uk 1, j 1. |
|
|
|
|
|
|||
U(x h) U(x h) 2hU (xi), U (x) |
U(x h) U(x h) |
– |
цен- |
|||||
|
||||||||
тральная разность. |
|
2h |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
U(x h) U(x) |
– правое разностное отношение. |
|
|
|
|||
|
|
|
|
|||||
U (x) |
h |
|
|
|
||||
|
U(x) U(x h) |
– левое разностное отношение. |
|
|
|
|||
|
|
|
|
|||||
U (x) |
|
|
|
|
||||
h
Метод граничных элементов (МГЭ) отличается от метода ко-
нечных элементов (МКЭ) тем, что он позволяет решать задачи с использованием дискретизации лишь границы области. В то время как МКЭ и МКР требуют дискретизации всей расчетной области и расчет проводится с определением значений функции на всех узлах сеток, в МГЭ предусмотрен предварительный переход от исходной краевой задачи для дифференциальных уравнений, описывающих процесс, например, теплопередачи или НДС детали к соотношениям, связывающим функции на границе области. Эти соотношения представляют собой граничные интегральные уравнения или особые функционалы. При этом число узлов уменьшается в два и более раз, возникает возможность выполнять расчеты для бесконечных областей, а также для решения задач, имеющих трещины, вычислять колебания волн в заливе и т.п. Однако данный метод пока наиболее эффективен для двумерных областей (на плоскости).
39
