
2390
.pdf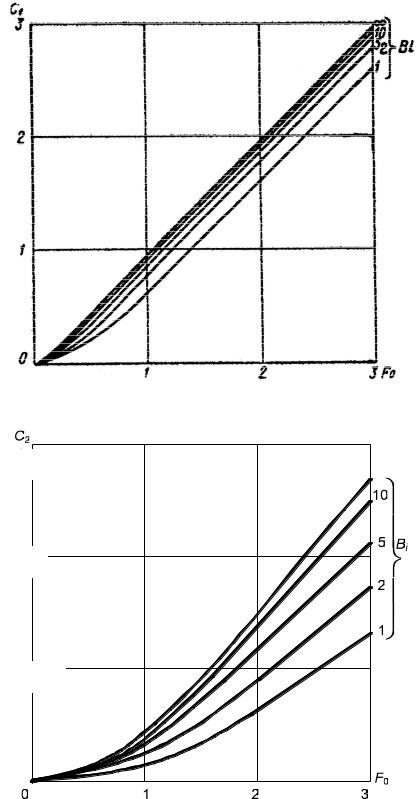
Рис. 2.5. Кривые С1 = f1(F0;Bi) для шара |
|
1,5 |
|
|
|
1 |
|
0,5 |
|
Рис. 2.6. Кривые C2 |
f2 (F0, Bi ) |
для неограниченной пластины |
|
49
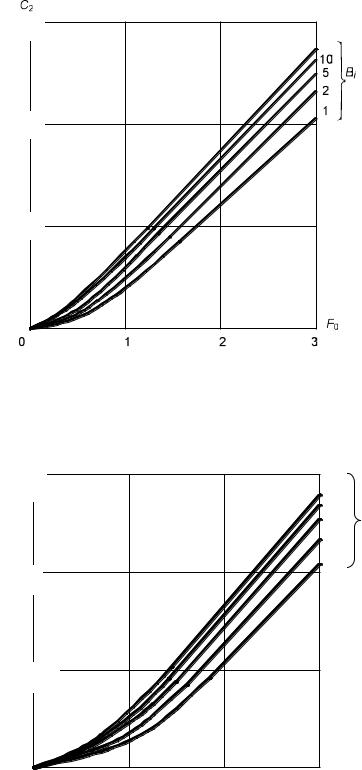
1,5 |
|
1 |
0,5 |
|
Рис. 2.7. Кривые C2 |
f2 (F0, Bi ) |
|
|
|
для неограниченного цилиндра |
|
|
|
С2 |
|
|
|
|
31,5 |
|
|
|
|
|
|
|
10 |
В |
|
|
|
5 |
i |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
21 |
|
|
|
|
1 |
|
|
|
|
0,5 |
|
|
|
|
|
|
|
F0 |
|
0 |
1 |
2 |
3 |
|
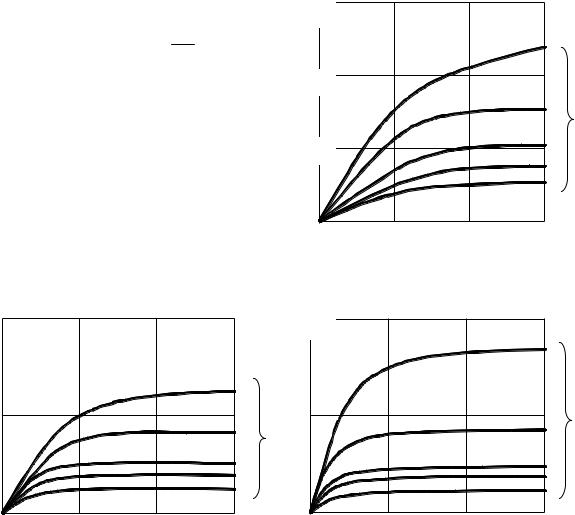
Рис. 2.8. Кривые C2 f2 (F0, Bi ) для шара
50
При изотермическом прогреве температура среды камеры постоянна и железобетонные или бетонные изделия прогреваются при постоянной температуре. В этом случае количество градусочасов, которое набирает изделие, определяем по формуле
|
|
из tиз из |
|
|
|
C3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
tиз tк R2 |
|
|
|
1,5 |
|
|
|
|
|
|
|
C3 , |
(2.14) |
|
|
|
1 |
|
|||
|
|
|
a |
|
|
|
2 |
|
|
|
|
где |
C3 f3(F0,Bi) |
вычисляем |
из |
|
|
|
|
||||
1 |
|
|
2 |
Bi |
|||||||
графиков на рис. 9…11; tиз темпе- |
|
|
|
||||||||
|
|
|
|
|
|||||||
ратура |
изотермического |
прогрева |
1 |
|
|
5 |
|
||||
изделия, °С; tк средняя температу- |
0,5 |
|
|
10 |
|
||||||
|
|
|
|
||||||||
|
|
|
∞ |
|
|||||||
ра изделия в конце периода подъёма |
|
|
|
|
|||||||
|
|
|
|
|
|||||||
температур, °С. |
|
|
|
|
0 |
1 |
2 |
F0 |
|
||
|
|
|
|
|
|
|
3 |
|
|||
|
|
|
|
|
|
Рис. 2.9. Кривые |
C3 f3(F0,Bi ) |
|
|
|
|
|
|
|
для неограниченной пластины |
||
С3 |
|
|
|
|
С3 |
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
0,5 |
|
|
|
Bi |
0,5 |
|
|
Bi |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
10 |
|
|
|
|
10 |
|
|
|
∞ |
|
|
|
|
∞ |
0 |
1 |
2 |
F0 |
|
0 |
1 |
2 |
F0 |
3 |
|
3 |
||||||
Рис. 2.10. Кривые C3 f3(F0,Bi ) |
Рис. 2.11. Кривые C3 f3(F0,Bi ) |
для неограниченного цилиндра |
для шара |
Пример 2.1. Определить удельную величину тепловыделения железобетонной панели R = 0,1 м на портландцементе марки 400, если известно:
количество цемента в 1 м3 бетона………………………….... Ц = 380 кг; водоцементное отношение…………………………………….. В/Ц = 0,5; начальная температура бетонной смеси…………………….... t0 = 15 С; скорость подъема температуры среды в камере.………….. b = 25 С/ч;
51

продолжительность подъёма температур…………………… под = 3 ч;
температура изотермической выдержки…………………..… tиз = 90 С; продолжительность изотермической выдержки…………….... из= 5 ч; средний за период нагрева коэффициент теплоотдачи…………………………………………… 1 58 Вт/(м2 С);
то же, за период изотермической выдержки……….. 1 81 Вт/(м2 С); коэффициент теплопроводности бетоннойсмеси….... 1,98 Вт/(м С);
плотность бетона свежеотформованной панели………. 2400 кг/м3;
удельная теплоёмкость бетона………………….… с = 1,05 кДж/(кг С).
Вычисляем коэффициент температуропроводности:
a |
3,6 |
|
1,98 3,6 |
0,0028 м2/ч. |
|
c |
1,05 2400 |
||||
|
|
|
Находим критерий Вi и F0 для периода подъема температур:
Bi |
R |
|
58 0,1 |
2,94, |
F0 |
a под |
|
0,0028 3 |
0,84. |
||
|
1,98 |
|
|
|
|
||||||
|
R2 |
0,12 |
|||||||||
По графикам (см. рис. 2.6) для полученных значений Вi и F0 находим величину С2 = 0,13, тогда количество градусочасов, которое наберёт панель, будет равно
|
|
|
|
|
bR2 |
|
|
|
|
|
|
|
25 0,12 0,13 |
|
|
|
|
|
|
t |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
3 80,5 |
. |
|||
|
0 |
|
2 |
|
|
|
|
С ч. |
|||||||||
|
|
|
a |
|
|
ïîä |
|
|
0,0028 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определяем критерий Вi для периода изотермического прогрева:
Bi из R 81 0,1 4,1.
1,98
Вычисляем среднюю температуру панели в конце периода подъема температур по формуле (2.10), в которой С1 определяем по кривым (см.
рис. 2.3):
tк |
t0 |
|
bR2 |
С1 |
15 |
25 0,12 |
0,38 48,9 |
С. |
a |
|
|||||||
|
|
|
|
0,0028 |
|
|
||
Вычисляем критерий F0 |
для изотермического режима: |
|
||||||
52
F0 |
a |
из |
|
0,0028 |
5 |
1,39. |
R |
2 |
2 |
|
|||
|
|
0,1 |
|
|
||
По кривым (см. рис. 2.9) находим для F0 = 1,39 и Вi = 4,1 С3 =0,482. По формуле (2.14) вычисляем количество градусочасов для изотермического режима:
|
из |
t |
|
t |
из |
t |
к |
|
R2 |
C |
3 |
90 5 90 48,9 |
0,12 0,482 |
379 |
0С ч |
. |
|
|
|||||||||||||||
|
|
из из |
|
|
|
a |
|
0,0028 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Общее количество градусочасов равно
под из 80,5 379 459,5 0С ч.
По номограмме (см. рис. 2.1) находим, что этому количеству градусочасов, марке цемента 400 и В/Ц = 0,5 соответствует тепловыделение
Qэ =238 кДж/кг.
Тепловыделение 1 м3 бетона будет равно
Qэбет QэЦ 238 380 90,44 103кДж.
2.3. Распределение температур и температурные перепады в бетонных и железобетонных изделиях в период подъёма температуры среды в тепловой установке
Цикл тепловлажностной обработки железобетонных изделий включает следующие этапы: подъём температуры паровоздушной среды (период подогрева), выдерживание изделий в камере при максимальной постоянной температуре (период изотермической выдержки), остывание изделий (период охлаждения).
Особое значение имеет расчёт температуры бетона в период подогрева, так как на этой стадии распределение температур по толщине бетона существенно влияет на его структурообразование, а также в процессе периода охлаждения, когда появляется опасность образования наружных трещин.
Температура в любой точке в любой момент времени с учётом тепловыделения определяется уравнениями:
– для неограниченной пластины
53
t x, t0 |
|
b m pi |
R2 |
2 x2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
2 |
|
|||||
|
1 |
|
|
|||||||
|
|
2a |
|
|
Bi R |
|
|
|
||
|
|
|
b m pi R2 |
|
|
An |
|
|
|
|
x |
n2F |
|
|
|
|
|
|
|
n2F |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos n |
|
|
|
|
|
e |
0 (tn |
t0 ) Ane |
0 ; |
|||||||||||||||||||
|
|
a |
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
n 1 |
|
|
n |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|||||||||||||
|
– для неограниченного цилиндра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
t r, t0 b |
b m pi R |
2 |
2 r2 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
4a |
|
|
|
|
B |
|
|
|
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||
|
|
b m p R2 |
|
|
A |
|
|
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||
|
|
|
|
a |
i |
|
|
|
|
|
|
n |
|
I0 n |
|
|
|
|
e nF0 (tn t0) Ane nF0 ; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
n 1 n2 |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
||||||||||||||||||
|
– для шара |
|
|
|
|
|
|
|
|
b m pi R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
r |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t r, t0 b |
|
|
6a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 B |
|
R2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
||
|
b m p |
R2 |
|
A |
R |
sin n |
r |
|
n2F |
|
|
|
|
|
|
|
|
|
|
|
|
|
n2F |
||||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
i |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
0 (tn |
t0 ) Ane |
0 , |
||||||||||||||||||
|
a |
|
2 |
|
|
|
|
|
|
|
|
n |
|
|
|||||||||||||||||||||||||||
|
|
|
n 1 |
n |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
||||||||||||||
(2.15)
(2.16)
(2.17)
где x, r координаты точки рассматриваемого тела; An, n постоянные,
зависящие от формы тела и критерия Вi; I0 функция Бесселя первого рода нулевого порядка; m – удельное тепловыделение бетона, ºC/ч; Pi – интенсивность испарения влаги из бетона, кг/м2 ч.
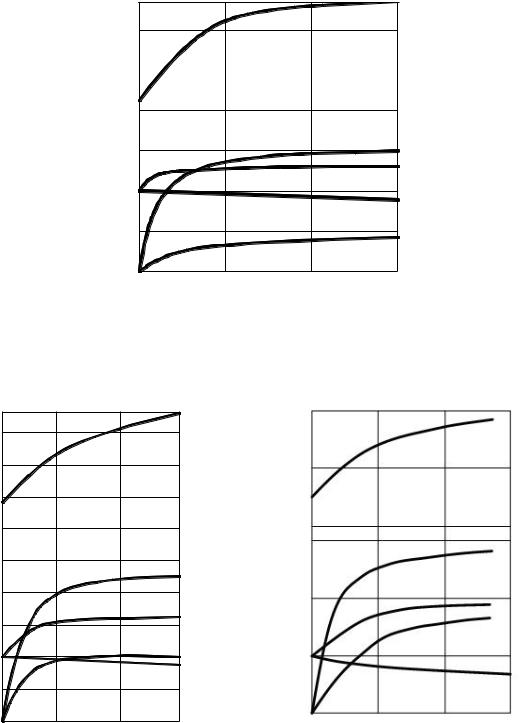
В данном решении число членов ряда может быть для практических расчётов ограниченным. При значениях критерия F0>0,2 можно ограничиться только первым членом ряда и соответственно значениями A1 и 1. При F0<0,2 достаточно взять первые два члена ряда и соответственно постоянные A1, A2 и 1, 2 . Значения этих постоянных в зависимости от Вi для неограниченной пластины, неограниченного цилиндра и шара приве-
дены на рис. 2.12…2.14.
54
μ,A |
|
|
μ2 |
|
|
|
|
|
|
4,0 |
|
|
|
|
3,0 |
|
|
|
|
1,5 |
|
|
|
μ1 |
|
|
|
|
А1 |
1,0 |
|
|
|
В1 |
|
|
|
|
|
0,5 |
|
|
|
А2 |
|
|
|
|
|
0 |
5 |
10 |
15 |
Вi |
|
||||
|
Рис. 2.12. Значения постоянных 1 , |
2 , |
||
|
A1, A2, В1 в зависимости от критерия Вi |
|||
|
для неограниченной пластины |
|
||
µ, А |
|
|
|
2 |
µ, А |
|
|
|
|
|
|
|
|
6,0 |
|
|
2 |
||
5,0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
4,5 |
|
|
|
|
5,0 |
|
|
|
|
4,0 |
|
|
|
|
|
|
|
|
|
3,5 |
|
|
|
|
4,0 |
|
|
|
|
|
|
|
|
|
3,0 |
|
|
1 |
|
2,5 |
|
|
|
1 |
|
|
|
||
2,0 |
|
|
|
|
|
|
|
||
|
|
|
|
2,0 |
|
|
А1 |
||
|
|
|
|
|
|
|
|||
1,5 |
|
|
|
А1 |
|
|
|
А2 |
|
1,0 |
|
|
|
А2 |
1,0 |
|
|
|
|
|
|
|
|
В1 |
|
|
|
||
|
|
|
|
|
|
|
|
||
0,5 |
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
Вi |
0 |
5 |
10 |
Вi |
|
0 |
5 |
|
10 |
15 |
15 |
||||
|
|
|
|
|
|||||
Рис. 2.13. Значения постоянных |
Рис. |
2.14. |
Значения |
постоян- |
|||||
ных µ1, µ2, А1, А2, B1 |
в зависи- |
||||||||
µ1, µ2, А1, А2, B1 |
в зависимости от |
||||||||
мости от критерия Вi |
для шара |
||||||||
критерия Вi |
для неограниченного |
||||||||
цилиндра |
|
|
|
|
|
|
|
|
|
55
В частном случае, если испарения влаги из бетона нет и начальная температура его равна температуре среды, т.е. ρi = 0; tн = t0, получаем:
– неограниченная пластина
t x, t0 b |
|
b m |
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
R |
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||||||||||||||
|
|
|
2a |
|
|
|
|
|
B |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||||
|
|
b m |
|
2 |
|
|
An |
|
|
|
|
|
|
|
|
|
|
|
x |
|
2F |
|
|
(2.18) |
||||||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
cos n |
|
|
e |
|
|
|
|
|
n 0 |
; |
|
|
||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
n 1 n2 |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
– неограниченный цилиндр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
t r, t0 b |
|
b m |
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
1 |
|
|
|
|
|
|
|
|
r |
|
|
|||||||||||||||||||||
|
|
|
4a |
|
|
|
|
|
|
B |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||||
|
|
|
b m |
A |
|
|
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
(2.19) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
I0 n |
|
|
e |
nF0 ; |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
a |
|
n 1 n2 |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
– шар |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t r, t0 b |
|
b m |
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
R |
1 |
|
|
|
|
|
|
|
r |
|
|
|||||||||||||||||||||||
|
|
|
4a |
|
|
|
|
|
|
|
|
B |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
||||
|
b m |
|
|
|
|
|
|
|
|
R |
|
|
|
|
sin( n |
|
r |
) |
|
|
|
|
|
(2.20) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
R2 |
|
An |
|
|
|
|
|
|
|
|
R |
e n2F0 . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
a |
|
|
n 1 n2 |
|
|
|
|
r |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В частном случае, когда испарение происходит только с верхней поверхности панели (панель находится в форме) и tн = t0, получаем
t x, t0 |
|
b m R2 |
2 x2 |
|
|||||
b |
|
1 |
|
|
|
|
|
|
|
2a |
|
|
2 |
||||||
|
|
|
B |
R |
|
|
|||
|
|
|
|
i |
|
|
|
||
|
|
|
b m R2 A |
|
|
|
|
|
|
|
x |
|
2 |
F |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
n |
cos n |
|
|
|
|
e |
n |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||
|
|
a |
|
|
|
|
|
R |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
n 1 n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
|
|
2 |
F |
|
|
|
|
|
|
|
|
|
|
B |
|
x |
|
|||||||
|
1 |
|
An cos n |
|
|
e |
n |
|
|
|
1 |
|
|
|
|
|
i |
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 n 1 |
|
|
R |
|
|
|
|
|
|
|
|
|
|
2 1 Bi R |
|
||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
F0 |
|
|
|
|
(2.21) |
|||||||
|
|
|
|
|
Ak1sin |
|
k1 |
|
|
e |
|
k1 |
|
|
|
, |
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|||||
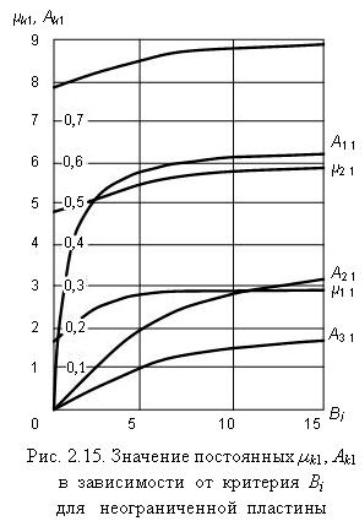
где – скрытая теплота испарения, кДж/кг; Аk1, µk1 – величины, зависящие от критерия Bi, определяемые по графикам на рис. 2.15.
56
Пример 2.2. Требуется определить температуру на поверхности и в середине (центре) железобетонной панели в конце периода подогрева в ямной камере, если известны следующие данные:
продолжительность периода подогрева……..…......................... τ1= 3 ч; начальная температура панели, равная начальной температуре среды…………..…….…......................................................... tн =t0=15 °С;
средний за 3 ч коэффициент теплообмена................. α =58 Вт/(м2 оС); коэффициент теплопроводности железобетона.........λ = 1,98 Вт/(м оС); удельная теплоёмкость железобетона ....................с =1,05 кДж/(кг оС); характерный размер панели, равный половине её
толщины .…. .…………………........................…..................…. R=0,1 м;
количество цемента марки 400 в 1 м3 бетонной смеси ….. Ц = 380 кг;
водоцементное отношение…………………………………..... В/Ц=0,5;
скорость подъёма температуры среды в камере …….….. b = 25 С /ч; плотность железобетона свежеотформованной панели...ρ =2400 кг/м3.
57
Вычисляем коэффициент температуропроводности:
a |
3,6 |
|
1,98 3,6 |
0,0028 м2/ч. |
|
c |
1,05 2400 |
||||
|
|
|
Находим критерий Bi и F0 для периода подъема температур:
B |
|
R |
|
|
58 0,1 |
2,94; |
||||
|
|
|
||||||||
i |
|
|
|
|
1,98 |
|
|
|
||
F0 |
а |
|
|
0,00278 3 |
0,834. |
|||||
R |
2 |
|
2 |
|
|
|||||
|
|
|
|
0,1 |
|
|
|
|||
По графикам (см. рис. 2.6) для полученных значений F0 и Bi находим величину С2 = 0,2. Подсчитываем величину т, характеризующую удельное тепловыделение цемента, по формуле
|
|
|
|
bR2 |
|
|
|
|
В |
0,44 |
|
bR2 |
|
|
||||
|
|
АЦ t0 |
|
|
C2 |
|
|
0,0023Qэ28 |
|
|
Ц t0 |
|
C2 |
|
|
|||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
a |
|
|
|
|
Ц |
|
|
a |
|
|
||||
m |
|
|
|
|
|
|
|
|
|
|
||||||||
|
c |
|
|
|
|
|
|
c |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
0,0023 420 0,50,44 380 15 |
25 0,1 |
|
0,2 |
|
|
|
|
|
|
||||||||
0,00278 |
|
|
|
|
(2.25) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
0,84 2400 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как F0 > 0,2, то при подсчёте температуры панели можно ограничиваться только первым членом бесконечного ряда, входящего в формулу (2.15) и коэффициентами A1 и µ1. По графикам (см. рис. 2.12) находим,
что для Bi = 2,94 µ1 = 1,19, А1=1,21.
Подставляем известные значения величин в формулу (2.15) и при условии x = R получаем температуру поверхности панели:
|
|
|
b m R2 |
1 |
|
|
|
A1 |
cos 1 |
e |
2F0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
t R, t0 b |
|
a |
|
|
|
|
|
|
2 |
|
; |
|||||||||||||||
|
|
|
|
Bi |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
25 3 0,12 |
1 |
|
|
|
1,21 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
t R,3 15 25 3 |
|
|
|
|
|
|
|
|
|
|
|
|
cos1,19 |
e |
1,19 |
0,834 |
61,2 оС. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
0,00278 |
2,94 |
1,192 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Температуру середины (центра) панели определяем по формуле |
||||||||||||||||||||||||||
(2.15) при условии х = 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t 0, t0 b |
b m R |
2 |
1 |
|
|
1 |
|
|
A |
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
e |
nF0 |
; |
|
||||||||
|
|
a |
|
2 |
|
Bi |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
58 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
