Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2187.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

3.84 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

Раздел II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

§ 1. Определение производной функции (видео 2)
Пусть функция y = f (x) определена в точке x0 и некоторой ее ок-
С
рестности, x – точка из этой окрестности. Введем обозначения: раз-
ность x – x0 обозначим через x и назовем приращением аргумента,
разность f(x) – f(x0) обозначим через y						и назовем приращением
функц	(р с. 37).
и
	бА
				Рис. 37
Итак, x= x – x0; y= f(x) – f(x0). Отсюда получаем равенство
	x = x0 + x, тогда				y= f(x0 + x) – f(x0).
Производной функции				f (x) в точке x0		И
						называется предел отно-
шения приращения функции к приращениюДаргумента, когда прира-
щение аргумента стремится к нулю.
Производная обозначается f (x0).
Итак,
f (x	0) lim	y	lim	f (x0	x) f (x0 )		lim	f (x) f (x0)	.

	x 0 x		x 0		x		x x0	x x0

Пример

Найти производную для функции f (x) = x 2 в точке x0 = 3.

f			f (3 x) f (3)					(3 x)2 32
	(3)	lim				lim
				x
		x 0				x 0		x
lim		9 6 x ( x)2 9			lim		6 x ( x)2

			x
	x 0				x 0			x
	lim (6 x) 6.
	x 0
Если
Спро зводная				f (x0) существует, то говорят, что функция f (x)

дифференц руема в точке x0. Установим связь между дифференцируемостью функц f (x) в точке x и ее непрерывностью в этой точке. Напомн м,бАчто функц я f (x) непрерывна0 в точке x0, если она определена в точке x0 некоторой ее окрестности, и выполняется равенство

lim f (x) f (x0).

x x0

Переформулируем определение, используя понятия приращения аргумента и приращения функции. Из приведенного равенства получаем

lim ( f (x) f (x0 )) 0;	lim ( f (x0 x) f (x0)) 0;
x x0	x 0

lim y 0.

Другими словами, функция f (x) непрерывна в точке x0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

x 0
Д
	И

Теорема. Если функция f(x) дифференцируема в точке x0, то она непрерывна в этой точке.

Замечание. Если в точке x0 функция f (x) непрерывна, то в этой точке функция может и не иметь производной, что подтверждается следующим примером.

Пример

Функция f (x) x непрерывна в точке x0=0, так как

lim x 0 0 .

x 0

Покажем, что эта функция не имеет производной в точке x0:

lim

, но

f (0) lim

x 0 x

ренциру

емав точке x0 = 0.

если

x 0;

поэтому lim

если x 0,

x 0 0

бА

а lim

знач

т, lim

не существует, т.е. f (x) не диффе-

x 0 0 x

x 0 x

Геометрический смысл производной

Рассмотрим геометрический смысл производной.

На рис. 38 изо ражен график непрерывной функции y = f (x).

f (x0 x)

f (x0)

x0 x

y = f(x)

Рис. 38

Точка M0 на графике имеет координаты (x0,

f (x0)), еще одна

точка графика M – координаты (x0 +

x, f(x0 +

x)). Прямая M0M

является секущей для линии y = f(x), она наклонена к оси Ox под углом .

Пусть f (x0) существует, то есть lim y – некоторое число. Из

x 0 x

M0MА получаем, что y tg (известно, что tg – угловой коэф-

фициент прямой M0M). Если x 0, то точка M движется по графику функц y = f (x), приближаясь к точке M0, при этом секущая

M0M, поворач ваясь вокруг точки M0, стремится занять предель-
коэффициент
ное положен е, то есть совпасть с касательной M0K, при этом
С( – угол между касательной M0K и осью Ox); tg = tg .
Так м образом, f (x0) lim		y	tg , но tg = k есть угловой

	бА
	x 0	x
коэфф ц	касательной M0K.	касательной к графику y = f (x) в
Итак,	угловой
точке с абсц ссой x0 равен производной функции f (x) в точке x0:
	f (x0) = k = tg .
В этом состоит геометрический смысл производной.
	Д
Очевидно, что уравнение касательной (рис. 39) имеет вид
	y – f (x0) = f (x0)(x – x0).
			И

Рис. 39

Уравнение нормали (см. рис. 39)		имеет вид
y – f (x0) =	1		(x – x0).

	f (x0 )
СM0

Переходим к рассмотрению механического смысла производ-

ной (видео 3).

Пусть матер альная точка движется прямолинейно неравномер-

но по закону S = f(t), где t – время; S – путь, проходимый точкой за
и
время t.
	M
бА
S0	S	S

Рис. 40

Пусть в момент времени t0 точка находилась в положении M0 (рис. 40). Поставим задачу: определить скорость материальной точки

в момент t0. Рассмотрим другой	момент времени	t0 + t. За время t0
пройденный точкой путь равен	S0 = f (t0), за (t0 +	t) пройдено рас-
стояние S = f(t0 + t) и точка оказалась в положении M, тогда за время
t пройден путь M0M и он равен
S – S0 = f (t0 + t) – f(t0) = S.
	И
Средняя скорость Vср за пpомежутокДвремени t равна			S	. Но
Средняя скорость Vср за пpомежутокДвремени t равна			t	. Но
			t

средняя скорость может быть различной, в зависимости от промежутка времени t. Скоростью V(t0) в момент времени t0 называется предел средней скорости Vср при t 0. Итак,

V(t0) lim S S (t0).

t 0 t

Производная от S = f(t) в момент времени t0 есть скорость в момент времени t0.

§ 2. Производные некоторых элементарных функций

Пусть функция y = f (x) определена на некотором промежутке X и f(x) дифференцируема в точке x0 X, то есть производная

f (x0) lim

существует.

x 0 x

Производная функция от функции f (x), по определению, имеет

вид

f (x x) f (x)

(x) lim

x 0

Выч сл м про зводные некоторых элементарных функций.

1. f(x) = с – постоянное число. Тогда (c)' = 0. Действительно,

f (x x) f (x)

lim

c c

lim

0 0.

f (x) lim

x 0

x 0 x

x 0

(x)' = 1. Действительно,

(x x) x

lim

lim 1 1.

(x) lim

x 0

бА

(

. Действительно,

x x

(

) lim

lim

x x x)

x 0

x 0 x(

lim

x 0

x x x 2 x

. Действительно,

			1	1
lim	f (x x) f (x)	lim	x x	x

	x		x
x 0		x 0

lim

x (x x)

lim

x 0 x(x x) x

x 0 x(x x)

(sin x)' = cos x. Действительно,

2sin

cos(x

)

(sin x)

lim

sin(x x) sin x

lim

x 0

бА

иsin

lim

lim cos(x

) 1 cos x cos x.

x 0

6. Аналогично доказывается, что (cos x)' = –sin x.

ln a. Действительно,

ax x ax

a x(a x

a x 1

) lim

lim

x 0

ax lna.

Здесь при вычислении предела использована эквивалентность

a 1~ lna (при 0).				x И
При a = e	получаем формулу e	x	e
				.

100

§ 3. Основные правила дифференцирования

Установим правила дифференцирования.

Теорема 1. Если функции u(x), v(x) дифференцируемы в точке x, то их сумма дифференцируема в этой точке, причем

(u(x) + v(x))' = u'(x)+v'(x).

Теорема 2. Если функции u(x), v(x) дифференцируемы в точке x,

то их про зведен е д фференцируемо в этой точке, причем

(u(x)v(x))' = u'(x)v(x) + u(x)v'(x).

ледств е. Постоянный множитель можно выносить за знак

, то есть

производной

(C f(x))' = C f (x).

Доказательство. Используем теорему 2:

(C f(x))' = C f x C f (x) = 0 f x C f (x) = C f (x).

Теорема 3. Если функции u(x), v(x) дифференцируемы в точке x

и v(x) 0, тобих частное дифференцируемоАв этой точке, причем

u(x)

u (x) v(x) u(x) v (x).

(x)

v(x)

С помощью теоремы 3 можно вычислить производные функций

tg x и ctg x.

Пример

Покажем, что

(tg x)

. Действительно,

cos2 x

sin x

(sin x) cos x sin x(cosx)

cos2

x sin2 x

(tg x)

cos

cos x

101

Итак, получили формулу

(tg x)

. Аналогично находит-

cos2 x

ся производная (ctg x)

sin2 x.

Пусть y = f (u(x)является сложной функцией, составленной из

функций y = f (u); u = (x), где u – промежуточный аргумент.

Теорема 4. Если функция u =

(x)имеет производную ux в

точке x, а функц я y = f (u) имеет производную yu

в точке u

= (x),

то сложная функц я y = f (u(x))

в точке x имеет производную yx ,

причемyx =

yu ux .

Иначе: про зводная сложной функции равна произведению

производной данной функции по промежуточному аргументу на про-

изводную промежуточного аргумента.

С помощью теоремы 4 найдем производную степенной функции

y x , где – постоянное число.

По свойствам

логарифмов

eln x

e ln x ,

поэтому

e ln xявляется сложной функцией от x:

y = e u ; u = ln x. По

теореме 4

бА

y (x ) yu ux

e ln x x

x 1.

Итак, получена формула

x x 1.

Теорема 5 (правило дифференцирования обратной функции). Пусть функция y = f (x) определена на промежутке X, непрерывна, монотонна (возрастает или убывает) и дифференцируема на X. Если ее производная yx в точке x не равна нулю, то обратная функция

x f 1( y) имеет производную xy в точке y , причем

102

На основании теоремы 5 можно получить следующие формулы:

(arcsinx)

1 x2

(arccosx)

1 x2

(arctgx)

бА2

1 x

(arcctgx)

1 x2 .

Введем понятия гипер олических функций, имеющих примене-

ние в математике и ее приложениях:

гиперболический синус

sh x

e x

;

гиперболический косинус

ch x

;

гиперболический тангенс

th x

;

Дe e

гиперболический котангенс

cth x

ex e x

Для гиперболических функций верны тождества

th x

sh x

;

cth x

ch x

; ch2x – sh2x =1.

ch x

sh x

103

Найдем производные гиперболических функций, при этом напомним, что (e –x)' = e –x (–1) = – e –x (как производная сложной функции):

(shx)

((e

)

chx.

) )

Итак,

(sh x)' = ch x.

Также доказывается, что ch x)' = sh x.

С2

x =1, то получаем

Так как ch

x – sh

(th x)

ch2 x.

Аналог чно можно показать, что

(cthx)

sh2x.

Совокупность полученных формул назовем таблицей производ-

ных:

бА

1. c 0.

9. arcsinx

1 x

2. xm mxm 1;

10. arccosx

1 x2

3. ax

ax lna;

11. arctgx

И1 x

4. loga x

;

12. arcctgx

xlna

1 x

104

13. (shx)' = chx.

lnx

cosx.

14. (chx)' = shx.

5. sin x

sin x.

15.

(th x)

6. cosx

7. tgx

cos2

16. (cthx)

sh x

8. ctgx

sin2 x

Основные свойства:

бА

u v

;

u v

;

yx = yu ux .

Примеры

Найти производные функций в примерах 1 – 4:

1. y

ex 2х

Решение.

Используем правило вынесения постоянного множи-

теля за знак производной и правило дифференцирования разности:

1 x

ex 2x ln2

e 2

e 2 ln 2

2. y lncosx .

105

Решение.

Используем

правило

дифференцирования

сложной

функции f g x

(g) g

(x):

cos x

(cos x)

( cos x)

cos x

cos x 2

cos x

sin x

tg x.

2cos x

представив

Замет м,

что этот результат можно было получить,

функц ю в в де y ln

cosx

lncosx.

бА

3. y e x

ln x.

Решен е.

Воспользуемся правилом дифференцирования

про-

изведен я двух функц й и производной сложной функции. Получим

-x

e x

ln x)

(lnx)

ln x

) ln x e

4. y arccos

Решение. Используем формулу производной сложной функции.

Получим

y (arctg

)

(

)

x4 1

5. Составить уравнения касательной и нормали к графику функ-

ции y sin 2x в точке x0

Решение.

уравнение

касательной

Используем

2π

;

y f (x0) f (x0)(x x0).

нашем

случае

f (x0) sin

106

f (x0) 2cos

2π

1. Подставляем в уравнение y

), от-

куда получим

y x

– уравнение касательной.

Запишем теперь уравнение нормали

f (x

)

(x x ).

f (x0)

, от-

Подстав м в это уравнение числовые данные

куда y x

– уравнение нормали.

Задачидля самостоятельного решения

Выч сл ть про зводные функций (прил. 6):

y 6cos x 7x 3ex 2x2 1.

y 2tgx 2x3

7ln x 21 6x .

y 3arcsinx 8ctgx 3x

6x10

81.

бy (2ln x x А3)(6e 3sin x cosx).

y (3arctg x 8x)(2tg x 6log5

x 4).

y 3sin x 4ln x.

3x2 6x 7

5tgx 8x 4

5ctgx 6ex

2x2 7

arctgx

y (3x2 6x 8)3.

10.

y sin(2x2 4x 5).

11.

y cos(4x ln x).

12.

y arctg(x2).

13.

y e2sin x cos x .

107

14.

y (4ex 3)7.

15.

y (sin x)3.

16.

y ln5 x.

17.

y arctg2x.

3x 8

18.

sin x

2x 3

19.

y sin

уравнения 6

20.

cos3 x

21.

Состав ть

касательной и нормали к графику

функц

y cos3x в точке x0

22.

Состав ть уравнения касательной и нормали к графику

функц

y xe3x в точке x0

23.

Составить уравнения касательной и нормали к графику

бА

функции

7 в точке

x0 2.

Ответы:

1. y

6sin x 7 3e

4x.

2(3x

6x 8)

(6x 6).

13.

2sinx cos x

(2cosx sin x).

17. y

arctg x

1 x2

21.

y 3x – уравнение касательной.

§ 4.

Дифференцирование

функций,

заданных неявно

и параметрически.

Логарифмическое

дифференцирование

Пусть переменные x, y связаны между собойИнекоторым уравнением F(x, y) = 0, причем y является функцией от x, тогда говорят, что функция y задана неявно.

Например, уравнение y3 – 5x2 – 3x = 0 задает неявно функцию y,

которую можно из этого уравнения выразить явно: y = 33x 5x2 . Неявное уравнение x2 + y2 = a2 неявно задает две явные функции:

108

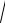y =a2 x2 и y = –a2 x2 .

Однако не всегда функции, заданные неявно, могут быть выражены явно. Так, из неявного уравнения y + x = 2siny нельзя выразить y явно.

Для нахождения производной y' неявно заданной функции надо найти производные по x от обеих частей этого уравнения, помня, что y – функц я от x, приравнять эти производные. Из полученного

уравнен я выраз ть y'.
Напр мер, найдем y' для функции x2			+ y2	= a2:
С	(x2 + y2)x = (a2)x	; 2x + 2y y' = 0,

отсюда y' = –x y.
и
бА

Пр мен м этот метод для нахождения производной для показа- тельно-степенной функции y = u(x)v(x), где u(x) > 0; u(x), v(x) – диффе-

ренцируемые функц .

Прологарифмируем равенство y = uv, получим ln y = v ln u.

Дифференцируем полученное равенство:
		1	y' = v' ln u + v	1		u',
			y' = v' ln u + v			u',
		y	Д
		y			u
откуда получаем
	y' = y(v' ln u + v			1 u').
						И

Подставим сюда y = u v, найдем производную y' = u v ln u v'+ v u v–1 u'.

Этот прием нахождения производной называется логарифмиче-

ским дифференцированием.

Пример

y xsin x (x > 0). Найти y'.

109

Решение. Прологарифмируем равенство ln y = sin x

ln x, полу-

чим (ln y)' = (sin x ln x)'. Теперь вычисляем производные и выражаем

y':

y' = cos x ln x + sin x

;

y' = xsin x

(cos x ln x + sin x

или

производную

xsin x 1.

xsin x cos x ln x + sin x

Замет м,

что

показательно-степенной функции

y = u(x)v(x), где u(x)

0; u(x),

v(x) – дифференцируемые функции,

способом

можно выч сл ть другим

. Предварительно преобразуем

функц ю:

y uv eln uv

ev ln u.

Теперь мы можем продифференцировать данную явно заданную

функцию как сложную.

v ln u

y e

ln u ln u e

ln u

u .

Покажем данный прием на примере.

Пример

y xsin x

(x > 0). Найти y'.

Решение. Преобразуем функцию:

y x

sin x

ln xsin x

sin x ln x

Дифференцируем ее теперь как сложную функцию:

y e	sin x ln x		e	sin x ln x
y e			e		sin x ln x =

110

=e	sin x ln x		1
		cosx ln x sin	x			=
		cosx ln x sin	x			=
					x
	=xsin x cosx ln x sin x		1	.
	=xsin x cosx ln x sin x			.
			x

Рассмотрим теперь параметрическое уравнение линии на плоскости, в котором переменные x, y являются функциями третьей пере-

менной t (называемой параметром):

x (t);

t X.

y g(t),

бА

Функц я x

= (t) на некотором интервале изменения t имеет об-

ратную

функц ю

t = 1(x).

Тогда

y = g( 1(x)). Пусть x = (t);

y = g(t) имеют производные, причем xt

По правилу дифференцирования сложной функции,

yx yt tx .

На основании

правила

дифференцирования обратной

функции

tx xt ,

поэтому

при x = (t).

Итак, производная параметрически заданной функции имеет вид

;

x (t).

Получена формула производной функции, заданной параметрически.

Примеры

1. Пусть функция y, зависящая от x, задана параметрически:

111

x acost;	0 t 2 .
	0 t 2 .
y bsint,

Найти yx .

bcost

Решение. yx

asint

= –

ctg t ; x acost .

Получ ли про зводную:

Найти

x acost;

ctg x.

угловой коэффициент k касательной к циклоиде в точке

M0, соответствующей значению параметра t0

Решение. Параметрическое уравнение циклоиды имеет вид

x a(t sint);

y a(1 cost).

Поэтомубy = a sin t;Аx = a (1 – cost);

asint

sint

a(1 cost) = (1 cost).

Итак, производная циклоиды –

это функция вида

x a(t sint);

sin t

1 cos t

Угловой коэффициент касательной в точке M0 равен значению

yx при t0

112

	sin				2
					2			2			2(2 2)			2	2 2
				2
k =	4	=					=			=			=			=		+1;
																	2


	1 cos		1			2		2	2			4 2			2
						2		2	2			4 2			2
						2
	4					2


С
k =	2+1.
3. Прод фференц ровать неявно заданную функцию
при
		2xy2	x2 y x2 2 0.
Решен е. Прод фференцируем обе части данного уравнения по
	бА
переменной x, уч тывая				этом, что y			является функцией аргумен-
та х. Получ м
(2xy2 x2 y x2 2)x			2y2 4xyy 2xy x2 y 2x 0.
Из этого равенства выразим производную yx :
		4xyy x2y 2xy 2y2 2x,
откуда					Д
				2xy 2y2 2x
		y			4xy x2 .			И
4. Продифференцировать функцию, заданную параметрически:
			x 2cost2;

			y sint 3t.
Решение. Используем правило дифференцирования функции,
заданной параметрически: yx					yt	. Получим
заданной параметрически: yx						. Получим
					xt

113

cost 3

3 cost

(sint 3t)

(2cost

2( sint

)

) 2t 4tsint

Итак,

3 cost

;

4tsint2

x 2cost

рифмическогоln y ln(sin x) ;

с помощью лога-

Найти про зводную функции y (sin x)sin x

Сд фференцирования.

бА

Решен

. Дана функция

y (sin x)sin x. Поэтому

sin x

(ln(sin x)

sin x

) ;

(sin xlnsin x) ;

y y(cos xlnsin x sin x

cos x

)

sin x

(sin x)sin x (cos xlnsin x sin x ctg x).

sin x

Продифференцируем функциюДy (sin x) иначе. Сначала

преобразуем функцию:

y (sin x)

sin x

ln sin x sinx

sin x ln sin x

Теперь используем формулу дифференцирования сложной

функции:

esin

x ln sin

x ln sin x (sin xlnsin x)

y (sin x)sin x

x esin

114

=esin x ln sin x (cos xlnsin x sin x cos x)

sin x

(sin x)sin x (cosxlnsin x sin x ctg x).

Получили, что

(sin x)sin x (cosxlnsin x sin x ctg x).

y (sin x)sin x

Задачи

для самостоятельного решения

1. Прод фференц ровать неявно заданную функцию:

) x2 y3 x2 y x2 1 0;

xy3

4xy

2 0;

в)

y x

y 0;

г)

y 3x y 0.

2. Продифференцировать функцию, заданную параметрически:

5t;

t 3;

x 2t

б)

x 2t

2 4t4 1;

4t3;

y 3t

y t2

6t;

;

в)

x 2t

г)

x 2t

;

y 2t 3t

y t

3. Найти производную показательно-степенной функции с по-

мощью логарифмического дифференцирования:

y (cosx)sin x ;

б) y (cosx)x ;

в)

y (sin x)

cos x

;

г)

Иln x

y (sin x) .

4. Исходя из определения производной, найти f

(0):

115

	2tgx 2sin x		, x 0;
a) f(x)=
		x2
		x 0;
0,

б) f(x)= 1 cos(xsin

x 0;

в) f(x)= 1 ln(1 3x

cos

) 1,

x 0;

бА

x 0;

г) f(x)= ln(1 sin(x

sin

)),

x 0;

lncos x

x 0;

д) f(x)=

x 0.

				3tcost;
5. Составить уравнение касательной к кривой			x	3tcost;

				3 sint
			y	3 sint

		И
в точке t =	.	Д
в точке t =	.	Д
2

6. Составить уравнение нормали к кривой в точке t = :

x 2(tsint cost);

y 2(sint tcost).

116

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20213.77 Mб62182.pdf
#
07.01.20213.79 Mб02183.pdf
#
07.01.20213.8 Mб182184.pdf
#
07.01.20213.8 Mб2952185.pdf
#
07.01.20213.82 Mб172186.pdf
#
07.01.20213.84 Mб72187.pdf
#
07.01.20213.85 Mб12188.pdf
#
07.01.20213.85 Mб162189.pdf
#
07.01.2021356.57 Кб0219.pdf
#
07.01.20213.86 Mб112190.pdf
#
07.01.20213.86 Mб152191.pdf

Раздел II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

§ 1. Определение производной функции (видео 2)