
- •Введение
- •Раздел I. ПРЕДЕЛЫ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
- •§ 1. Математическая и логическая символика
- •§ 2. Множества
- •§ 3. Функции
- •§ 4. Числовые последовательности
- •§ 5. Предел функции
- •§ 6. Основные свойства пределов функции
- •§ 7. Замечательные пределы
- •§ 8. Вычисление пределов
- •§ 9. Непрерывность функции в точке
- •Вопросы и задания для самопроверки по разделу «Пределы. Непрерывность функции одной действительной переменной»
- •Контрольная работа по разделу «Пределы. Непрерывность функции одной действительной переменной»
- •Раздел II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- •§ 1. Определение производной функции
- •Тесты по теме «Вычисление производной функции одной действительной переменной»
- •§ 5. Основные теоремы о дифференцируемых функциях
- •§ 6. Дифференциал функции
- •§ 9. Нахождения наибольшего и наименьшего значений функции на отрезке
- •§ 12. Формула Тейлора
- •Вопросы и задания для самопроверки к разделу II
- •Тесты по разделу «Дифференциальное исчисление функции одной действительной переменной»
- •Контрольные работы по разделу «Дифференциальное исчисление»
- •Приложение 3
- •Приложение 5
- •Приложение 6
§ 9. Нахождения наибольшего и наименьшего значений функции на отрезке
|
Наибольшее M и наименьшее m значения функции y f (x) на |
|||||||||||
отрезке находятся по плану: |
|
|
|
|
||||||||
С |
|
|
|
|
|
|
|
|||||
|
1. Найти критические точки первого типа. |
|
||||||||||
|
2. |
Выбрать те критические точки первого типа, что принадлежат |
||||||||||
данному отрезку. |
|
|
|
|
|
|
|
|||||
|
3. |
Выч сл ть значения функции на концах отрезка и в выбран- |
||||||||||
Найти |
|
|
|
|
||||||||
ных кр т ческ х точках. |
|
|
|
|
|
|
||||||
|
4. Из всех найденных значений выбрать самое большое – это M |
|||||||||||
и самое малое – это m. |
|
|
|
|
|
|
||||||
|
|
|
|
бА |
||||||||
|
Пр мер |
|
|
|
|
|
|
|
||||
|
|
|
|
|
на |
ольшее |
и |
наименьшее |
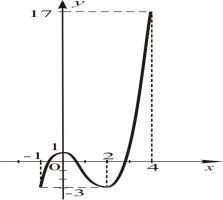
значения функции |
|||
y x |
3 |
3x |
2 |
1 на |
1;4 |
|
(рис. 50). |
|
|
|||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Д |
||
|
|
|
|
|
|
|
|
|
|
Рис. 50 |
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Вычисляем производную y 3x2 |
6x, затем решаем уравне- |
|||||||||
ние 3x |
2 6x 0; |
x |
0; x |
2 |
2 – нашли критические точки пер- |
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
вого рода. |
|
|
|
|
|
|
|
|
|
|||
|
2. |
x1 ; x2 1;4 . Обе критические точки принадлежат данному |
||||||||||
отрезку. |
|
|
|
|
|
|
|
|
|
|||
|
3. |
Находим значения функции на концах отрезка и в критиче- |
||||||||||
ских точках:y( 1) 3; |
y(4) 17; y(0) 1; y(2) 3. |
|||||||||||
|
4. |
yнаибольшее(4) 17; |
yнаименьшее( 1) |
y(2) |
3. |
|||||||
160
§ 10. Схема исследования функции и построения графика
хема исследования функции и построения графика:
1. |
Найти область определения функции. |
|||||||||
2. |
Выяснить, является ли функция чётной, нечётной или общего |
|||||||||
С |
|
|
|
|
|
|
|
|||
вида. |
|
|
|
|
|
|
|
|
|
|
3. |
Найти точки пересечения графика с осями координат. |
|||||||||
4. |
Найти ас мптоты графика функции (вертикальные, горизон- |
|||||||||
тальные, наклонные). |
|
|
|
|
|
|||||
Найти |
|
|
|
|||||||
5. |
|
первую производную функции. Определить интервалы |
||||||||
возрастан я, убыван я, точки экстремума функции. |
||||||||||
6. |
|
вторую производную функции. Определить интервалы |
||||||||
выпуклости (вогнутости) и точки перегиба графика функции. |
||||||||||
7. |
На основан |
|
|
проведённого исследования выбрать масштаб, |
||||||
постро ть граф к функции. |
|
|
|
|||||||
|
|
Четность и нечетность функции |
||||||||
Функция |
y f (x) называется четной, если y ( x) y x . Гра- |
|||||||||
фик четной функции симметричен относительно оси Oy. |
||||||||||
Пример |
|
|
|
|
1 |
|
|
|||
Функции y x2 ; |
y cos x; y |
– |
четные. |
|||||||
|
||||||||||
|
|
|
|
|
Д |
|||||
|
|
|
|
|
|
x |
2 |
|
|
|
ФункциябАy f (x) называется нечетной, если y ( x) y x . |
||||||||||
График нечетной функции симметричен относительно начала коор- |
||||||||||
динат. |
|
|
|
|
|
|
|
|
|
|
Пример |
|
|
|
1 |
|
|
||||
Функции |
y x |
3 |
; |
– нечетные. |
||||||
|
y sin x; y |
|
||||||||
|
|
|
|
|
|
x |
|
|
||
|
|
Асимптоты графика функции |
||||||||
Прямая x a |
|
называется вертикальнойИасимптотой кривой |
||||||||
y f (x), если |
lim |
|
f (x) или |
|
lim |
f (x) . |
||||
|
|
x a 0 |
|
|
x a 0 |
|||||
Прямая x a может быть вертикальной асимптотой графика функции, только если при x a функция не определена.
161
Прямая |
y = |
kx+ b |
является |
наклонной асимптотой кривой |
|||
y f (x), если |
|
|
|
|
|
|
|
k |
lim |
|
f (x) |
0; |
b |
lim ( f (x) k x) 0. |
|
|
|
||||||
|
x x |
|
|
x |
|||
Замечание. |
Функция y f (x) |
может иметь разные правую и |
|||||
левую наклонные ас мптоты. |
|
|
|||||
Частным случаем наклонной асимптоты является горизонталь- |
|||||||
Сная ас мптота. Прямая y b является горизонтальной асимптотой, |
|||||||
k 0. |
|
|
|
|
|
|
|
|
|
|
|
|
b lim |
f x 0. |
|
еслиx |
|
|
|||||
Замечан я |
|
|
|
|
|
|
|
1. Функц я y f (x) |
может иметь разные правую и левую гори- |
||||||
зонтальные асимптоты. |
|
|
|
||||
2. Функция |
y f (x) не может иметь одновременно и наклон- |
||||||
ную и горизонтальную правую (левую) асимптоты. |
|||||||
тервале (– , + ), поэтому вертикальных асимптот нет.
Пример |
|
Найти асимптоты линии y = e x – x. |
|
бА |
|
Решение. Функция f (x) = ex – x определена, непрерывна на ин- |
|
|
Дe |
Найдем наклонные асимптоты, для этого вычислим пределы:
|
|
k lim |
|
f (x) |
= lim |
( |
x |
– 1) = , |
|
|
|
|
|
|
|||||
|
|
x |
x |
||||||
|
|
x |
x |
|
|
||||
|
ex |
|
|
|
|
|
что при x правой |
||
так как lim |
|
= . Отсюда следует, |
|||||||
|
|||||||||
x |
x |
|
|
|
|
|
И |
||
наклонной асимптоты нет. |
|
|
|
|
|
||||
Так как |
lim ex x , то правой горизонтальной асимптоты |
||||||||
уфункции нет.
Ищем левые наклонные асимптоты:
162

k lim |
|
f (x) |
|
|
|
|
|
ex |
|
|
|
|
|
|
|
|
ex |
|
|
отсюда k = –1. |
|||||||||||
|
|
|
|
|
= lim |
|
|
( |
|
|
– 1) = –1, так как |
lim |
|
|
|
|
= 0, |
||||||||||||||
|
|
|
x |
|
|
|
|
x |
|||||||||||||||||||||||
x |
x |
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||
Далее, b lim |
|
|
(f(x) – k x) = |
lim |
(e x – x + x) = lim e x = 0, зна- |
||||||||||||||||||||||||||
чит, b = 0. |
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
||||||||
|
|
|
|
|
|
|
y = – x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Итак, |
прямая |
|
|
|
|
есть левая |
наклонная асимптота при |
||||||||||||||||||||||||
x для графика функции y = e x – x. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Левой гор зонтальной асимптоты нет, так как есть левая на- |
|||||||||||||||||||||||||||||||
клонная ас мптота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
меры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
С |
сследование |
функции |
и |
построить ее |
|
график: |
|||||||||||||||||||||||||
1. |
|
|
|
|
|
|
|
||||||||||||||||||||||||
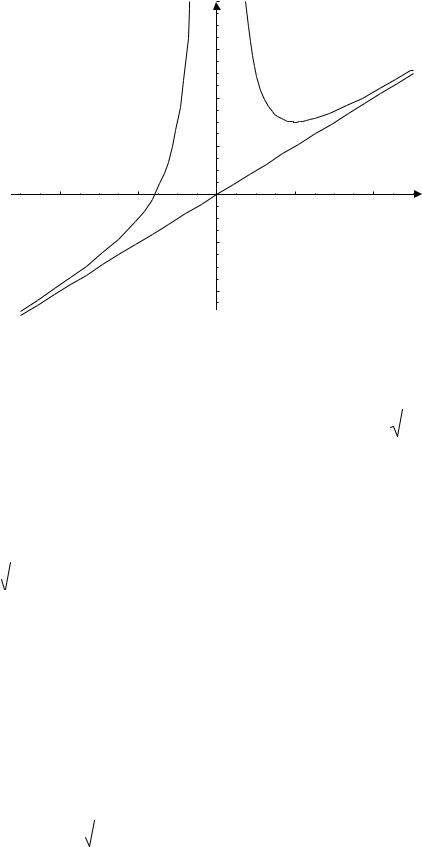
y x3 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Провести1. Наход м ласть определения: х 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2.Исследуем на |
четность. |
f ( x) |
x3 |
4 |
f (x), |
следова- |
|||||||||||||||||||||||||
x2 |
|
|
|||||||||||||||||||||||||||||
тельно, это функция о щего вида. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3. Находим точки пересечения графика функции с координат- |
|||||||||||||||||||||||||||||||
ными осями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 4 0; |
|
|
|
|
|||||||||||
|
|
|
|
c осью Ох: y = |
0, |
|
поэтому |
x 3 |
|
. Точка |
|||||||||||||||||||||
|
|
|
|
4 |
|||||||||||||||||||||||||||
(3 |
|
;0) точка пересечения графика с осью Ох; |
|
|
|
|
|||||||||||||||||||||||||
4 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
бА |
|
|
|
|
|||||||||||||||||||||||
|
|
|
с осью Оу: x = 0; |
y не существует. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4. |
Находим асимптоты графика функции. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Сначала исследуем функцию на непрерывность. Функция опре- |
|||||||||||||||||||||||||||||||
делена и непрерывна при |
всех |
|
х 0. Точка х = 0 – |
точка |
|
разры- |
|||||||||||||||||||||||||
ва 2-го |
рода, |
так как |
|
|
|
|
|
|
Д |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
lim |
y lim |
|
x3 4 |
|
; lim y |
lim |
x3 4 |
. |
|
|
|||||||||||||||||||
|
|
|
|
x2 |
|
|
x2 |
|
|
||||||||||||||||||||||
|
x 0 0 |
x 0 |
|
|
|
x 0 0 |
x 0 |
|
|
|
|
|
|
||||||||||||||||||
Так как в точке |
х=0 |
|
функция имеетИбесконечный разрыв, то |
||||||||||||||||||||||||||||
прямая х = 0 является вертикальной асимптотой. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Наклонные асимптоты ищем в виде y = kx + b. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
k lim |
|
|
f (x) |
|
|
x3 4 |
|
|
|
|
4 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
lim 1 |
|
|
|
1; |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x x |
x x3 |
x |
|
|
x3 |
|
|
|
|
||||||||||||||||
163
|
|
|
|
|
|
|
|
x3 4 |
|
|
|
|
4 |
|
|
|
|
|
||||||
|
|
|
b lim ( f (x) kx) lim |
|
|
|
|
|
x |
lim |
|
|
0. |
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
x |
|
|
|
x x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Наклонная асимптота у = х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
С |
интервалы монотонности функции и точки экстре- |
|||||||||||||||||||||||
|
5. Находим |
|||||||||||||||||||||||
|
мума с помощью первой производной. Исследование оформляем в |
|||||||||||||||||||||||
|
виде табл. 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|||||
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
||||||||||
|
Определяем кр т ческие точки 1-го рода: |
y |
1 x3 |
; y = 0 |
||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
х = 2; у = при х = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Точка х = 0 не может ыть критической точкой функции, так как |
|||||||||||||||||||||||
|
|
|
|
бА |
|
|
|
|
|
|
|
|
||||||||||||
|
в этой точке функц я не определена. Точка x |
2 |
– критическая точ- |
|||||||||||||||||||||
|
ка 1-го рода. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
х |
|
|
|
(- ,0) |
|
0 |
|
|
|
|
|
(0,2) |
|
|
|
2 |
|
|
|
(2,+ ) |
|
|
|
|
y |
|
|
|
+ |
|
|
|
|
|
|
– |
|
|
|
|
0 |
|
|
|
+ |
|
|
|
|
y |
|
|
|
Возрастает |
|
Не |
|
|
|
|
Убывает |
|
|
|
3 |
|
|
|
Возрастает |
|
||
|
|
|
|
|
|
|
|
существует |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Итак, точка (2, 3) является точкой минимума. Экстремум функ- |
|||||||||||||||||||||||
|
ции ymin 3. |
|
|
Д |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6. Находим |
интервалы |
выпуклости и точки перегиба графика |
|||||||||||||||||||||
|
функции с помощью второй производной. |
И |
||||||||||||||||||||||
|
|
|
24 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
y |
x4 > 0 при любом х 0, следовательно, |
функция |
вогнутая |
||||||||||||||||||||
на всей области определения.
7. Построим график функции, начертив сначала наклонную асимптоту , отметив точку экстремума и точку пересечения с осью Ох
(рис. 51).
164
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|||||||
и |
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
-4 |
|
|
|
-2 |
|
|
|
0 |
|
|
2 |
|
4 |
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
бА |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 51 |
|
|
|
|
|
|
|
2. Провести полное исследование функции |
y 3 |
6x2 x3 |
и по- |
||||||||||||||||||
строить её график. |
|
|
|
|
Д |
||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
||||||||||||
1. Область определения функции |
|
( ; ). |
|
|
|
||||||||||||||||
2. |
|
Исследуем |
|
функцию |
на |
четность, |
нечетность: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
f ( x) 3 |
6x2 |
x3 |
|
f (x), следовательно, это функция общего вида. |
|||||||||||||||||
3. При x 0 |
|
|
|
|
|
|
|
|
|
|
И |
||||||||||
|
находим, что y 0, то есть |
О(0,0) – точка пересе- |
|||||||||||||||||||
чения с осью Oy; |
|
при y 0 получаем, |
что x 0 и |
x 6. так, точки |
|||||||||||||||||
О(0,0) |
и M 6,0 |
) |
– точки пересечения с осью Ox |
. |
|
|
|
||||||||||||||
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Ищем асимптоты: вертикальных нет, так как у функции нет |
|||||||||||||||||||||
точек разрыва. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Наклонная асимптота – это прямая y = kx+ b, где |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k lim |
f (x) |
|
|
|
3 |
6x2 x3 |
|
1; |
|
|
|
|
|
|
|
||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
x |
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
165

b lim |
( f (x) k x) lim(3 |
6x2 x3 |
x) 2, |
|
|
|
|
|
|
|
|
|
||||||||||||||
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значит, |
y x 2 – наклонная асимптота. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Горизонтальных асимптот нет, так как есть наклонная. |
||||||||||||||||||||||||||
5. Первая производная имеет вид |
y |
|
x(4 x) |
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
(x2 (6 x)) |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Реш м уравнен е |
|
x(4 x) |
|
|
0 |
и найдём критические точки |
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||
С |
|
(x2 (6 x)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
первого рода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бА |
|
|
|
|
|||||||||||||||||||||
x1 0: |
y не существует в этой точке, но меняет знак при |
|||||||||||||||||||||||||
переходе через неё с м нуса на плюс, значит, |
( ) |
= 0– точка мини- |
||||||||||||||||||||||||
y 0 |
||||||||||||||||||||||||||
мума (особый экстремум); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x2 4: |
y 0 в этой точке и меняет знак при переходе че- |
||||||||||||||||||||||||
рез неё с плюса на минус, значит, y(4) 3,2 |
– точка максимума; |
|||||||||||||||||||||||||
|
x3 6: |
y не существует в этой точке, не меняет знак при |
||||||||||||||||||||||||
переходе через точку, значит, экстремума в этой точке нет. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
Д |
|||||||||||||||||||
6. |
Вторая производная равна y |
|
|
|
|
8 |
|
|
|
. |
|
|
|
|
||||||||||||
|
4 |
|
|
5 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
(6 x) |
3 |
|
|
|
|
|
|
|
|||
Решим уравнение |
|
|
8 |
|
|
|
|
0 |
и найдём критические точки |
|||||||||||||||||
4 |
|
|
5 |
|
||||||||||||||||||||||
|
|
|
x |
3 |
(6 x) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
второго рода: |
y не существует в этой точке, |
|
|
|
|
|
||||||||||||||||||||
|
x3 6: |
меняет знак с ми- |
||||||||||||||||||||||||
нуса на плюс при переходе через точку, значит, y |
( ) |
|
|
|
||||||||||||||||||||||
6 = 0 – точка пе- |
||||||||||||||||||||||||||
региба; |
x1 0: исследована выше. |
|
|
|
|
|
И |
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
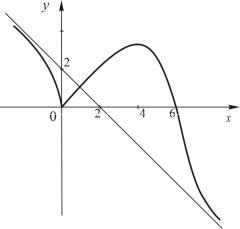
7. Построим график (рис. 52).
166
и |
Рис. 52 |
|
|
|
|
|
|
|
|||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
§ 11. Прав ло Лопиталя |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
бА |
|
|
0 |
|
|||||||||||||||||||
Теорема Лоп таля (раскрытие неопределенностей типа |
|
). |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
Пусть функц f(x), g(x) определены, непрерывны и дифферен- |
|||||||||||||||||||||||
цируемы в точке x0 |
|
некоторой ее окрестности, причем g'(x) 0 для |
|||||||||||||||||||||
любого x из этой окрестности, и пусть f(x), g(x) – бесконечно малые |
|||||||||||||||||||||||
при x x0. |
Если предел |
lim |
|
|
|
f (x) |
|
существует, |
то существует и |
||||||||||||||
|
|
|
g (x) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|||||
предел lim |
f (x) |
, причем |
|
|
|
Д |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x x0 |
g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
lim |
|
f (x) |
= |
lim |
f (x) . |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x x0 g(x) |
x x0 |
g (x) |
|
|
|
|
||||||||||||
Прием вычисления пределов, основанный на теореме Лопиталя, |
|||||||||||||||||||||||
называется правилом Лопиталя. |
|
|
|
И |
|||||||||||||||||||
Пример |
|
|
|
|
1 cos3x |
|
|
|
|
|
|
||||||||||||
Найти предел |
lim |
. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
x 0 2x |
|
|
|
|
|
|
|
|
|
g(x) = 2x удовле- |
|||||||||
Решение. Поскольку функции f (x) =1 – cos3x; |
|||||||||||||||||||||||
творяют условию теоремы Лопиталя, то |
|
|
|
|
|
|
|
||||||||||||||||
lim |
1 cos3x |
= lim |
(1 cos3x) |
= lim |
3sin3x |
= 0. |
|||||||||||||||||
|
2x |
|
|
|
|
||||||||||||||||||
x 0 |
|
|
|
x 0 |
|
|
|
(2x) |
|
x 0 2 |
|
|
|
|
|||||||||
167
Замечания
1. Теорема Лопиталя справедлива и при раскрытии неопреде-
ленности вида |
|
. Неопределенности 1 ;00 |
; 0 ; и другие |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
сначала нужно преобразовать к виду |
|
|
|
|
или |
|
|
|
, а затем приме- |
||||||||||||||||||||||||||||||
нить правило Лопиталя. |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пр мер |
|
|
|
|
|
|
lim x2 ln x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Найти предел |
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
x 0 1/ x2 |
|
||||||||||||||||||||||||
виду |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решен е. Так как limln x = , то имеем неопределенность типа |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
|
||||
(0 ). Преобразуем ее к |
|
|
|
|
: |
lim x2ln x (0 )= lim |
|
. |
|||||||||||||||||||||||||||||||
|
бАx 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Теперь пр мен м правило Лопиталя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
lnx |
|
|
|
|
|
(lnx) |
|
|
|
|
1/ x |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|||||||||||||
lim |
|
|
2 |
= |
lim |
|
|
|
|
|
|
= lim |
|
|
|
3 |
= lim |
|
|
|
|
= 0. |
|
|
|
||||||||||||||
x 0 1/ x |
|
|
|
|
|
|
x 0 1/ x2 |
|
x 0 |
2/ x |
|
|
|
x 0 |
|
|
|
2 |
|
|
|
||||||||||||||||||
Итак, lim x2 ln x = 0. |
|
|
Д |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2. Правило Лопиталя можно применять несколько раз при вы- |
|||||||||||||||||||||||||||||||||||||||
числении одного предела. |
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||||||||||||
Пример |
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Найти предел lim |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x 0 ctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. При x 0 и x > 0 |
limln x = ; limctg x = , следова- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|||||||
тельно, имеем отношение двух бесконечно больших при x 0+ и не- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
определенность вида |
|
|
|
. Вычислим предел по правилу Лопиталя: |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
lim |
ln x |
|
|
= lim |
|
|
1/ x |
|
= –lim |
|
sin2 x 0 |
|
|
= |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 sin2 |
|
|
|
x |
|
0 |
|
|
|
|
|
|
||||||||||||||||||||
x 0 |
ctgx |
|
|
x 0 |
|
x |
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
168
