1.

lim

x

2

2x 24

;

2.

lim

1 cos2x

;

e3x

2

x2 36

x 6

x 0

1

С

4x2

2x2

1 x 3

1

3.

lim

;

;

2

3x 1 5

4. lim

4x

x 8

x

lim

3x2 4x 6

5.

.

и

x

5x2 36

§ 9. Непрерывность функции в точке

Функц я y f x

называется непрерывной в точке а, если она

определена в некоторой окрестности точки a и lim

f x f a .

Пределы справа

слева:

x a

lim f x lim f x предел справа (рис. 15);

x a

x a

x a

Д

а

бАРис. 15

lim f x lim f x предел слева (рис. 16).

x a

x a

И

y

A

B

lim f x В

a

f x A

x

lim

x a

A B

x a

С

Рис. 17

Развёрнутое определение непрерывности

и

непрерывной в точке а, если

Функц я y f x является

1) определено значение функции в точке а;

2) существуют конечные односторонние пределы

lim

f x ; lim f x ;

x a

x a

3) эти пределы равны между собой:

lim

f x lim f x ;

x a

x a

4) этибАпределы равны f (a): lim f x lim f x f a

(рис.

x a

x a

18).

Д

y

f а

x

a

И

Свойства непрерывных функций

Теорема 1. Если f x и g x непрерывны в точке а, то

1)

f x g x сумма (разность) непрерывна в точке а;

2)

f x g x произведение непрерывно в точке а;

3)

f x

отношение непрерывно в

точке

а при

условии

g x

g a 0.

y x

Теорема 2 (непрерывность сложной функции): если

непрерывна в точке а и

z f y

непрерывна в точке b a , то

С

x непрерывна в точке а.

сложная функц я z f

Теорема 3. Все элементарные функции непрерывны в своей об-

определен я.

Теорема Вейерштрасса. Если функция непрерывна на отрезке

ласти

a;b , то она дост гает на этом отрезке своего наименьшего и наи-

большего значен й: x1,x2

a,b : f x1 m,

f x2 M .

Следствие теоремы Вейерштрасса. Если функция непрерывна

на

отрезке

a;b ,

то

она

ограничена

на

этом

отрезке:

C :

f x

C на a,b .

Замечание. Для открытого интервала (а, b) теорема Вейершт-

расса неверна.

бА

a;b , то

Теорема Коши. Если функция непрерывна на отрезке

она принимает все промежуточные значения между наибольшим и

наименьшим значениями: k m,M x0 a,b : f x0 k.

Следствие теоремы Коши. Если функция непрерывна на от-

Д

резке a;b и принимает на концах отрезка значения противополож-

ных знаков, то внутри отрезка найдется хотя бы одна точка, в которой

она обращается в нуль: x0

a,b : f x0 0.

§ 10. Точки разрыва графика функцииИи их классификация

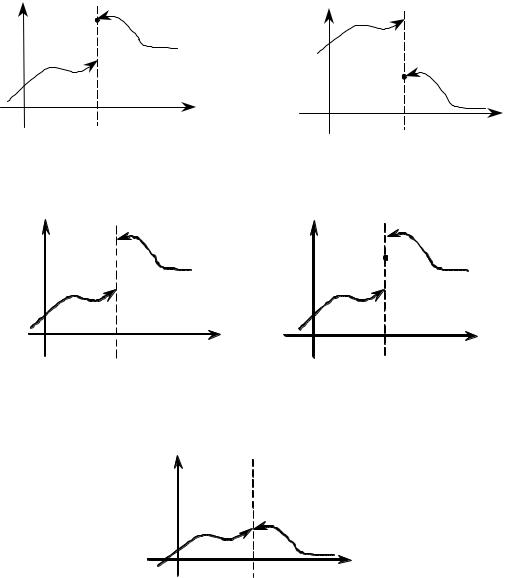
Графики функций с разрывами первого рода имеют вид, изо-

браженный на рис. 19 23.

y

f a

y

f a

x

x

a

a

СР с. 19

Рис. 20

y

y

f a

f a

и

не существует

x

x

a

a

Рис. 21

Рис. 22

y

бА

f

a не существует

(устранимый разрыв)

x

Дa

Рис. 23

Разрыв, изображенный на рис. 23, называется устранимым раз-

И

рывом. Для устранения разрыва достаточно доопределить функцию в

точке a: f a lim

f x lim

f x .

x a

x a

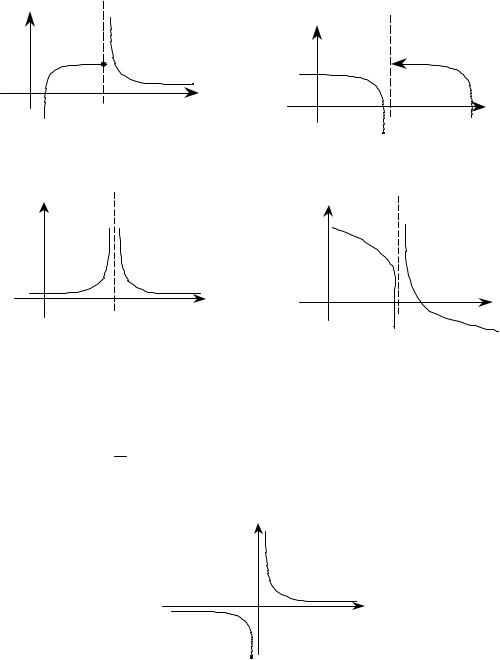
Точка разрыва а называется точкой разрыва второго рода, если

нарушается условие 2 непрерывности функции, то есть

lim

f x и (или) lim

f x .

x a

x a

Графики функций с разрывами второго рода показаны на рис.

24 27.

y

y

С

x

x

a

a

Р с. 24

Рис. 25

y

y

и

x

x

a

Рис. 26

Рис. 27

Пример

бА

Функция y

1

не определена при x 0. В этой точке она имеет

x

lim f x ; lim f x (рис. 28).

разрыв второго рода.

x 0

x 0

y

Д

Разрыв второго рода

x

Рис. 28

И

Примеры

Определить разрывы функций, изображенных на рис. 29 31.

и

Рис. 29

СНа р с. 29 зо ражен разрыв первого рода (скачок), не устрани-

мый в точке x0 . Нарушен пункт 3 определения непрерывности:

б

lim

f x

A; lim

f x B; A,B = const; A B.

x x0 0

f x

x x0 0

Функц я

в точке x0

имеет скачок, равный B A.

2.

А

Д

Рис. 30

рушены условия 1 и 4 развернутого определения непрерывности:

f x0

не существует, то есть

И

f x0 lim f x .

3.

x x0

lim

f (x) или

lim f (x) .

x x0

x x0

Такой разрыв часто называют бесконечным.

Примеры

1. Определ ть точки разрыва графика функции

и

С

2

,

x 1;

2x

1

y(x)

, 1 x 3;

x 2

бА

x

2,

3 x .

Решен е.

Функц я задана с помощью трех функцийy 2 x2;

y

1

; y x 2. При этом функции y 2 x2

и y x 2 непрерыв-

x 2

1

ны, функция y

не определена и поэтому разрывна при x 2.

x 2

Д

Исследуем вид разрыва в точке

x 2

и в точках

x 1; x 3, в

которых стыкуются графики указанных выше функций.

a) x 2.

Вычисляем односторонние пределы

lim

1

;

lim

1

.

x 2 x 2

И

x 2 x 2

рода;

Пределы бесконечные, значит,

x 2

точка разрыва второго

б) x 1.

Найдем односторонние пределы:

lim f (x) lim

2x2 2;

lim f (x) lim

1

1.

x 1 0

x 1 0

x 1 0

x 1 0 x 2

x 1

Пределы слева и справа конечны, но не равны, поэтому в точке

функция имеет разрыв первого рода (скачок);

lim f (x) lim

1

1;

lim

f (x) lim

x 2 1.

x 3 0

x 3 0 x 2

x 3 0

x 3 0

Пределы слева и справа конечны и равны. Кроме того, функция

определена при

x 3

y(3) 3 2 1, поэтому точка

x 3

точка

непрерывности функц .

односторонние

x3

4

2. Определ ть точки разрыва функции y

4x2

.

С

Решен . Функц я определена на всей числовой оси,

кроме

бА

2

точки х = 0.

Исследуем поведение функции в окрестности точки х = 0. Для

этого выч сл м

пределы

lim y

x3

4

y lim

x3

4

lim

;

lim

.

x 0 0

x 0 0 4x2

x 0 0

x 0 0 4x2

прямая х = 0 является вертикальной асимптотой графика функции.

Д

3. Определить точки разрыва функции

y

2x 1

.

(x 1)

Решение. Область определения функции

D(y) = x ;1 1; .

Заданная функция непрерывна всюду, кроме точки x =1. Вычис-

лим её односторонние пределы в этой точке:

lim

2x 1

;

lim

2x 1

.

2

(x 1)

(x

И2

x 1 0

x 1 0

1)

x 4

x3 2

x 5

С

1. y

x 7

;

2. y

;

3. y

x 6 4

;

x 3

4

x 2

4

4. y 2

x 1

;

5. y

x 1 (x 5)

;

6. y 4

x 3

;

и

3x

x 4

x 2

2 x2

1

7. y

;

8.y 2x 1;

9. y

;

x 3 (x 6)

5

бА

2x

,

x

1;

1

10. y(x)

,

1 x 5;

x 4

5 x ;

x,

x

2

,

x 2;

11. y(x)

2x

3

3x 2, 2 x ;

x

,

x 0;

5x

И

3

2

12. y(x)

,

0 x 5;

x 4

Д

1

, 5 x .

9

Ответы:

1. x 7 точка разрыва второго рода.

3. x 6 точка разрыва второго рода.

5. x 1; x 5 точки разрыва второго рода.

12. x 0 точка разрыва первого рода;

x 4 точка разрыва

второго рода; x 5 точка непрерывности.

одной действительной переменной»

Функции и их свойства

1. Дана функция y

x2

8x 16 6. Тогда её областью значе-

ний является множество …

(–1; + );

( ; );

6; );

6; ).

ции

из области определения функ-

С2. На большее целое значение x

y

3x 4 log0,3(7 x) равно…

5;

бА

6;

–1;

–6.

3. На меньшее целое значение x из области определения функ-

ции y lg(x 1,7)

x 3,5 3

x 5 равно …

3;

2;

4;

5.

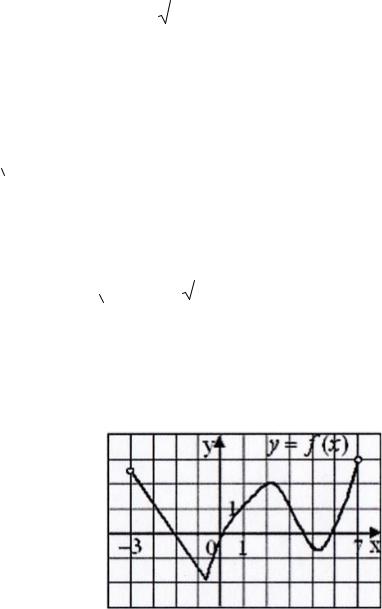
4. На рис. 32 изображен график функции y f (x).

Д

Рис. 32

И

Тогда при переходе от x 2 к

x 2

приращение y рав-

но…

0;

1;

2;

–1.

5.

Дана функция

y

8 x

. Тогда её областью

определения

является множество …

x 5

(5;8 ;

( ;5) 8; );

( 5;8);

( 5;8 .

6.

Для функции y x2

3x 1 в точке x 1 задано приращение

аргумента x=1.

Тогда соответствующее приращение функции y

равно…

С

5;

–6.

6;

–4;

7.

функции

y 4

(x 3)3

является про-

межуток…

определения

( ;3 ;

3; );

( ; 3);

( 3; ).

8. Пусть

f (x) sinx.

Тогда сложная функция g( f (x)) четная,

Областью

если функция g(x) задается формулами …

Укажите не менее двух вариантов ответа.

g(x) x5;

g(x) 6x;

g(x) 3x2

1;

g(x) x4 .

9. Пусть

А

f (x) sinx.

Тогда сложная функцияg( f (x)) четная,

если функция g(x)задается формулами …

Укажите не менее двух вариантов ответа.

3

Д

g(x) x 5;

g(x)

;

g(x) ex

; g(x) 6x4 1.

x2

10. Образом отрезка 3; 0 при отображении

f 2x 7 являет-

ся интервал…

И

0; 6 ;

13; 6 ;

13; 6 ;

13; 6 .

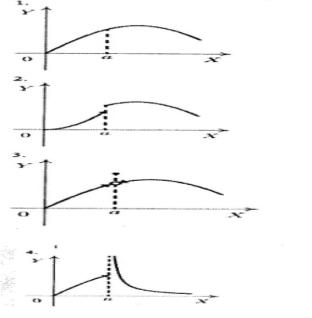
11. Для дробно-рациональной функции

y

x

2 x 2

точками

x2 3x

разрыва являются…

Укажите не менее двух вариантов ответа.

х = 0;

x = 1;

x = 3;

x = – 3.

x2

12. Для дробно-рациональной функции y

4

точками

2x2

x

разрыва являются…

Укаж те не менее двух вариантов ответа.

С

x = 0;

x = – 2.

х = – 0.5;

x = 2;

13.

разрыва функции y

x 4

являются точки…

Точками

x(x 5)

Укаж те не менее двух вариантов ответа.

x = 4;

x = –5;

x = 0;

x = 5.

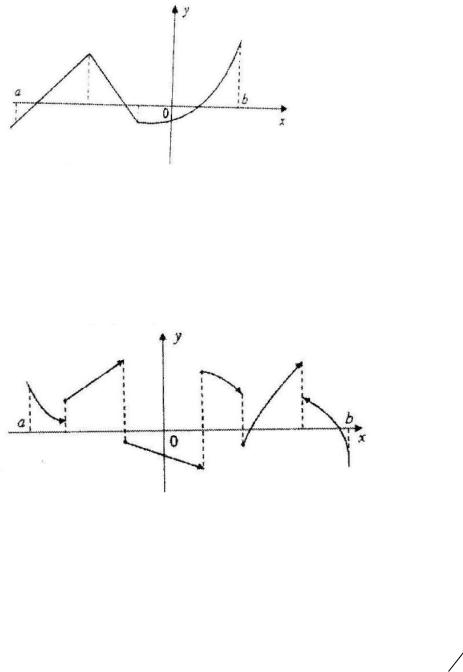
14. Установите соответствие между графиком функции (рис.

33) и характером точки х = a.

бА

–точка устранимого разрыва;

–точка разрыва 1-го рода;

Д

– точка максимума;

–точка разрыва 2-го рода;

И

15. Точками разрыва функции y

x 3

являются точки…

x(x 1)

Укажите не менее двух вариантов ответа.

x = 0;

x = –1;

x = 2;

x = – 3.

С

16. Число точек экстремума функции, заданной на отрезке a;b

(рис. 34), равно…

и

бА

Рис. 34

0;

1;

2;

3.

17. Число точек разрыва функции, заданной на отрезке a;b

(рис. 35), равно…

Д

Рис. 35

И

3;

4;

5;

6.

18. Установите соответствие между функцией и ее точкой раз-

рыва.

2. y 2

1

;

3. y 2

1

;

4. y 1 2 x .

1. y 1 ;

1

ln x

x x 1

x 2x 1

1;

0;

–1;

–2;

.

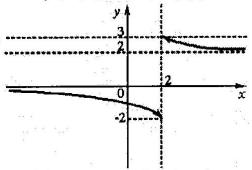
19. Если графику функции y f x (рис. 36) соответствует ус-

ловие lim f (x) 2, то значение a

равно…

x a

С

и

бА

Рис. 36

2;

;

3;

–2.

Пределы функций

1. Установите соответствие между пределами функций и их зна-

чениями.

Д

sin3x2

e4x

1

tg3x

1.lim

;

2.

lim

x

;

3. lim

.

x 0 2x

x 0

x 0 x3

0;

;

4;

;

3.

И

2. Установите соответствие между пределами функций и их зна-

чениями.

1.

lim

3x3

5x2 1

;

2.

lim

5x2

6x 3

;

7x 2

4x 1

x 4x3

x 7x3

3.

lim

2x3

5x 3

;

4.

lim

8x4

6x2 3

.

5x 8

x x2 5x 1

x x4

8;

0;

;

3

;

5

.

4

7

3

3.

Если lim

f (x) 1, то

равен…

lim f (x)sin2x

x 0

f