§ 3. Функции

множество Y называется правило, по которому каждому числу x из

множества X однозначно соответствует некоторое число y из множе-

С

X называется областью определения функции,

ства Y. Множество

множество Y называется областью значений.

Обозначен я:

функцию2. Для функц y =

x2 1 областью определения является

f

: X Y ;

f

X Y; y f x .

Пр меры

y x2 1. Тогда X , ее об-

1. Рассмотр м

бА

ластьопределен я;

Y

1, о ластьзначений.

множество X ; 1 & 1; ,множество значений Y 0, .

2

x, если x 0;

sin

здесь X = R, Y ; 1 .

3. y =

1

,

если x 0,

x

3.

y loga x логарифмическая a 0; a 1 .

4.

y sin x;

5.

y cosx;

6.

y tg x;

тригонометрические функции.

С

7.

y ctg x.

8.

y arcsinx;

9.

y arccosx;

обратные тригонометрические функции.

Операции

10.

y arctg x;

11.

y arcctg x.

над функциями

бА

Функц

можно складывать, вычитать, перемножать, делить.

Пр меры

1.

y

2x2 sin x

функция образована умножением функций

y 2x2

и y

2

sin x .

1

x2

2.

y

функция получена делением функций

y x2

и

cosx

1

y2 cos x.

Д

f

Примеры сложных функций:

И

1.

z sin x2 y x2; z sin y .

2.

z sin x 2 y sin x; z y2 .

3.

u tg log2 x3 y x3; z log2 y;

u tg z .

определения

которой является множество натуральных чисел 1, 2,

3, … . Элементы (члены) последовательности записываются в виде

С

f 1 , f 2 , f 3 , ;

ли an a1, a2, a3, ;

xn x1, x2, x3, .

Пр меры

1 , то есть a 1;

1

1

1. a

a

;

a

; .

n

2

n

1

2

3

3

ли

2.

an

1 n ,

то

есть

a1 1; a2

1; a3 1, ; a51 1;

a200 1,... .

3. an 1 , то есть a1

1;a2

a3 1, .

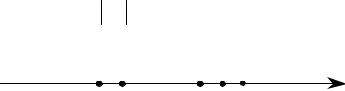
Последовательность an называется ограниченной, если суще-

ствует число М, такое, что

an

M при всех n

(рис. 4).

бА

(

an

)

х

М

0

М

Рис. 4

Пример

Д

an

n2 неограниченная последовательность.

Число a

называется пределом последовательностиИx , если

n

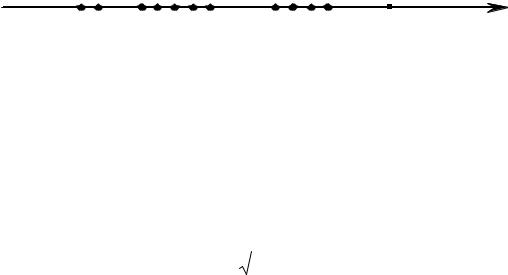
для любого числа 0

существует номер N , такой, что для всех

n N выполняется неравенство

xn a

(рис. 5).

Обозначение: a lim xn.

n

(

а

х

(

)

)

2

1

Рис. 5

Последовательность n

называется бесконечно малой (б. м.),

если lim n 0.

n

Пр мер

С

1

1

1

1

, k

0 ;

;

;

; б.м. последовательности.

nk

n

n2

n

Свойства . м. последовательностей:

и

1.

lim xn

a xn a .м.

x б

б.м.

2. Если an и n

.м., то an bn

А

Последовательность an называется положительно бесконеч-

но большой (п. б. б.), если для любого числа М > 0 существует номер

N (M), такой, что при всех n N

Двыполняется неравенство a M .

n

Обозначение:

lim an (п. б. б.).

И

Пример

n

n2 п. б. б.

Последовательность an называется отрицательно бесконечно

большой (о. б. б.),

если для любого числа М< 0 существует номер

Обозначение: lim an .

С

n

Пример

1 nn2 это не п. б. б., не о. б. б., а б. б. последовательность.

Если 1

1

Основные теоремы о последовательностях, имеющих предел

Теорема 1 (связь

.м. и .

. последовательностей):

1.

an .м., то

1

б.б.

1

.

б

0

an

2. Если an .

., то

. м.

0

.

an

А

Теорема 2. Если lim xn a , то

xn ограниченна.

n

Теорема 3. Если

lim xn a;

lim xn b, то a b. (Если после-

n

n

довательность имеет предел, то он единственный.)

Теорема 4. Если lim xn a;

lim yn b, то

n

n

И

1.

lim xn yn a b;

n

Д

2.

lim xn yn a b;

n

xn

a

3. при b 0

lim

;

n yn

b

4. lim

cx c lim x

n

, где c const.

n

n

n

Теорема 5.

Если

lim xn a;

lim yn

b,

причем xn yn при

n

n