2039

13.Первый закон термодинамики (закон сохранения энергии в

термодинамических процессах): Q = U + А, или δQ = dU + δА, где δQ – бесконечно малое количество теплоты; dU – приращение внутренней энергии; δА = p∙dV – бесконечно малая работа сил давления газа, обусловленная приращением объёма dV.

14. Взаимосвязь теплоёмкостей C=c M ;

где Ст – теплоёмкость тела, С и с – молярная и удельная теплоёмкости; ν – количество вещества; m – масса; М – молярная масса.

где Ацикла – суммарная работа сил давления газа во всех процессах цикла; Qподв – количество подведённой теплоты; ηмах – максимальный

КПД двигателя, работающего по циклу Карно; Т1 – температура

Qотв – количество отведённой теплоты; Азатр – затраченная работа.

где Qподв – количество теплоты, полученной нагреваемым помещением.

6 Существует несколько различных формулировок второго закона термодинамики.

40

6. ФИЗИКА КОНДЕНСИРОВАННОГО СОСТОЯНИЯ

жидкости (или газа) создают давление, одинаковое в любой точке жидкости (или газа).

где S – площадь поперечного сечения потока жидкости (или газа).

5.Сила сопротивления при движении сферического тела в

жидкости (закон Стокса) F c = 6 π η r υ,

где η – динамическая вязкость; r – радиус тела; υ – скорость тела.

6. Кинематическая вязкость жидкости ν = η/ρ.

7.Поверхностное натяжение (определение) σ= Fl , или σ= AS ,

где F – сила поверхностного натяжения; l – длина границы поверхностного слоя; A – работа сил поверхностного натяжения, совершаемая при изменении площади поверхности жидкости на величину S .

8. Высота подъёма жидкости в капилляре радиуса R при условии полного смачивания h = 2σ /(ρ gR).

9.Добавочное давление под изогнутой поверхностью жидкости

где R1 и R2 – радиусы кривизны поверхности, измеренные во взаимно перпендикулярных плоскостях.

10.Механическое напряжение при продольной упругой

деформации (закон Гука) σ = ε E ,

где σ = F/S ; F – растягивающая или сжимающая продольная нагрузка: S – площадь поперечного сечения твёрдого тела; l – длина тела (без нагрузки); х – деформация; ε = x/l – относительная деформация.

11. Формула Вульфа – Брэггов 2 d sin θm = m λ ,

где d – расстояние между атомными плоскостями; θm – угол скольжения рентгеновских лучей, соответствующий m-му дифракционному максимуму; m – номер максимума; λ – длина волны.

41

12. Расстояние d между соседними узлами кристаллической

решётки и число n атомов в элементарной ячейке

где а – размер элементарной ячейки (a3 = V0 – объём ячейки).

13.Зависимость сопротивления полупроводников от темпе-

где ∆E – ширина запрещенной зоны; С – постоянная величина для данного полупроводника; k – постоянная Больцмана; Т – температура.

которых ещё возможен фотоэффект; ∆E – ширина запрещенной зоны; h – постоянная Планка; с – скорость света в вакууме.

где νm – максимальная частота колебаний атомов (граница спектра фононов); k – постоянная Больцмана; ΘD – температура Дебая.

17. Молярная теплоёмкость твёрдого тела при низких темпе-

ратурах (T << ΘD)

R – молярная газовая постоянная; Т – температура вещества; ΘD – характеристическая температура Дебая для данного вещества.

19. Молярная теплоёмкость кристаллических твёрдых тел при высоких температурах (T >> ΘD) C=3 R na ,

где na – число атомов в молекуле твёрдого соединения.

20. Контактные разности потенциалов в замкнутой цепи

где k – постоянная Больцмана; Тa и Тb – температуры контактов в замкнутой цепи двух металлов или полупроводников; n1 и n2 – концентрации электронов; A1 и A2 – работы выхода электрона.

21. ТермоЭДС Т = Ua + Ub, или т = с·(Тa – Тb), где с – удельная термоЭДС; (Тa – Тb) – разность температур контактов.

42

VI. Контрольные задания и примеры решения

1. Механика

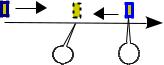
Пример 1. Скорость прямолинейного движения тела вдоль оси

Х задана уравнением υx = 4 – t2, где υx – проекция скорости на ось Х, м/с; t – время, с. Определить пройденный путь и перемещение тела за промежуток времени от t1 = 0 до t2 = 3 с.

времени модуль скорости сначала убывает до нуля, затем, когда проекция скорости на ось Х меняет знак (направление вектора υ меняется на противоположное), скорость по модулю увеличивается. В таких случаях, когда направление движения меняется, пройденный

t 2

dx = υx dt => x2−x1 = ∫υx dt .

t 1

Пусть координата тела равна нулю в начале отсчёта времени т. е. x1 = 0 при t1 = 0. Тогда координата тела в конце третьей секунды

Модуль перемещения тела за промежуток времени [0; 3 c] составляет |x2 – x1| = (3 – 0) м = 3 м.

Момент времени t = t*, когда скорость становится равной нулю (υ* = 0) и проекция скорости меняет знак, определим из уравнения

0 = 4 – t*2 => t* = ±2 с.

43

x * = 4 2 − 13 23 = 243 −83 = 163 .

Величина х* равна пути, пройденному за две секунды, т. е. х* = s0-2 , поскольку отсчёт времени начался, когда тело находилось в начале координат (x0 = 0), и направление движения не менялось.

В промежутке от t* = 2 до t2 = 3 c, когда тело двигалось в обратном направлении, изменение координаты тела также равно пройденному пути, т. е. s2-3 = |х3 – х*|. Таким образом, s2-3 = |3 – 5⅓| м = 2⅓ м, а весь пройденный путь s = s0-2 + s2-3 = 5⅓ + 2⅓ ; s = 7⅔ м.

Ответ. За промежуток времени [0; 3 c] тело переместилось на 3 м, пройдя путь 7⅔ м.

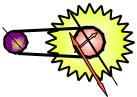
Пример 2. Дисковая пила приводится в движение электродви-

гателем посредством ремённой передачи (рис. 2). Диаметры шкивов: D1 = 25 мм; D2 = 50 мм; диаметр диска D = 300 мм. Двигатель начинает вращаться с частотой n = 10t, где n – частота, с-1; t – время, с. Найти линейную скорость υ*, нормальное an* и тангенциальное aτ* ускорения зубьев пилы

в момент времени t* = 1 с.

В момент времени t* = 1 с, an* = 15π2 = 148 м/с2.

44

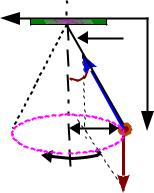
Пример 3. Небольшой грузик подвешен к потолку на длинной

невесомой нити. Кратковременным воздействием заставляют грузик двигаться по окружности в горизонтальной плоскости. При этом нить описывает конус высотой h = 2,3 м вокруг вертикальной оси (рис. 3). Найти период обращения грузика.

Решение. Если пренебречь сопротивлением воздуха, то модуль скорости υ грузика можно считать постоянным. Период обращения

Пример 4. Трамвайный вагон массой m = 5,0 т движется

прямолинейно. От остановки до остановки ускорение вагона изменяется по закону aх = 5 – 0,05х, где aх – проекция ускорения на ось Х, м/с2; х – координата вагона. Найти работу всех сил, действующих на вагон на всём пути, расстояние между остановками, максимальную скорость, время разгона.

45

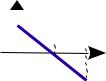
пересекающую ось абсцисс в точке х = ½ℓ (рис. 4). Скорость вагона сначала возрастает, пока ах > 0, затем, после половины пути, убывает. Максимум скорости достигается при ах = 0, когда прекращается разгон и начинается торможение.

Правая часть уравнения равна нулю, поскольку К1 = К2 = 0. Левая часть, представляющая собой суммарную работу всех сил на всём пути, также равна нулю. (Сопротивление движению пренебрежимо

46

Максимальную скорость будем искать, полагая, что её максимум, а следовательно, и максимум кинетической энергии Km достигаются на середине пути, в точке с координатой х = l/2.

Согласно теореме об изменении кинетической энергии

среднее ускорение; t* – время разгона. Учитывая линейность функции

Чтобы убедиться в правильности расчётов с использованием среднего ускорения, найдём путь s* за время t*, полагая движение равнопеременным с ускорением а 7 и начальной скоростью υ0 = 0.

За время разгона трамвай проходит путь s* = 100 м, равный половине расстояния между остановками.

Пример 5. Тело движется в вязкой среде по закону s = 3,0t2, где s – пройденный путь, м; t – время, с. На тело действует сила сопротивления F = 20υ2, где F – сила, Н; υ – скорость, м/с. Найти работу данной силы в промежутке времени от 0 до 10 с.

t = 10 с

7Использование среднего значения аргумента функции, когда она изменяется линейно, позволяет при решении ряда задач обойтись без интегрирования.

47

Сила сопротивления всегда направлена в сторону, противоположную перемещению, т. е. α = π рад и cos π = –1, следовательно

Найдём скорость движения тела как производную пути по времени, υ = 6t и, подставив её в формулу силы, F = 20·υ2, получим

F =20(6 t)2 .

Так как по условию s = 3,0t2, то ds = 6,0t·dt и элементарная работа

δ A =−(720t 2) (6,0 t dt) =−4320 t3 dt.

Ответ. Работа силы сопротивления А = –11 МДж.

Пример 6. Перемещение тела массой 10 кг совершается под

Так как a= ddtυ (по определению), то d υ = a dt и υ = ∫a dt .

48

Пример 7. Две платформы собственной массой по 400 кг

катятся по инерции навстречу друг другу по параллельным рельсам со скоростями υ01 = υ02 = 2,0 м/с. На одной из них лежит груз 100 кг. Определить: а) скорости платформ после того, как они поравняются и груз будет переброшен с одной на другую; б) изменение кинетической энергии данной системы тел.

(рис. 5). Трение мало, сила тяжести уравновешивается силой реакции рельсов, Считая замкнутой систему тел, включающую две платформы и груз, в данной системе отсчёта можно применить закон сохранения

Условия сохранения импульса относительно оси Х выполняются также для каждой из двух систем взаимодействующих тел: “платформа1 – груз” и “платформа2 – груз”, поскольку проекции внешних сил на ось Х равны нулю.

переброски не могут изменить проекции скоростей обоих тел на ось Х, так они действуют перпендикулярно оси Х.

где υ01 и υ1 – скорости первой платформы до и после переброски груза; υ0гр – скорость груза, проекция вектора которой на ось Х не изменяется под действием внутренних сил в системе “платформа1 – груз”.

49