1692

Корни находятся в два этапа: первый – отделение корней, т.е. нахождение отрезка [a, b], содержащего один корень уравнения; второй

– уточнение значения корней на найденных отрезках с заданной точ-

знак первой производной, то внутри этого отрезка находится один корень уравнения. Отделение корней можно осуществить различными способами.

1.Составляют таблицу значений функции y F(x) на выбранном отрезке изменения аргумента. Для отделения корня необходимо, чтобы на концах выделенного отрезка функция имела разные знаки и была монотонна. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства первой производной. От заданной функции F(x) найдем F (x) и вычислим ее

значения на концах отрезка [a, b], если F (a)*F (b) 0, функция F(x) монотонна.

2.Строят график функции y F(x) на отрезке изменения x; точка пересечения графика с осью ox даст нам корень уравнения. Для последующего уточнения корня возьмем окрестности корня и обозначим их [a, b].

3.Уравнение F(x) 0 заменяют равносильным ему F1(x) F2(x), строят два графика y1 F1(x) и y2 F2 (x). Абсцисса точки пересечения этих графиков, спроецированная на ось x, даст нам отрезок [a, b], внутри которого находится корень уравнения F(x) 0.

2.Методы решения нелинейных уравнений

2.1.Метод деления пополам (метод бисекций)

Задача. Найти решение нелинейного уравнения F(x) 0 с точностью .

Метод состоит в следующем: в результате отделения корня найден отрезок [a, b], в котором расположено искомое значение корня. В качестве начального приближения корня возьмем значение co=(b+a)/2. Далее исследуем значения F(x) на концах отрезков [a, co] и [co, b]. Тот из них, на концах которого F(x) примет значения разных знаков, содержит искомый корень. Поэтому его принимают в качестве нового

21

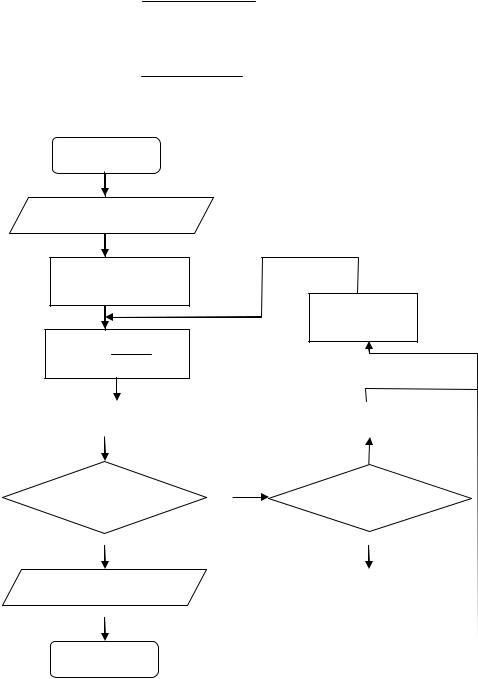
нием корня. Соединим точки А и В прямой, т.е. проведем хорду. Таким образом, получим b1, которое является приближением корня.

Воспользуемся уравнением пучка прямых, проходящих через точ-

ку B(b0, F(b0)).

y–y0=k(x–x0), y–F(b0)=k(x–b0).

Хорда должна проходить через точку A(a0, F(a0)), т.е.

k F(a0) F(b0) . a0 b0

Запишем уравнение прямой

y F(b0 ) F(a0 ) F(b0 )(x b0 ). a0 b0

Начало

Ввод a, b, i = 0, ε

Вычисле-

ниеF(a)

i = i +1

с a b

2

Конец

Рис. 2

23

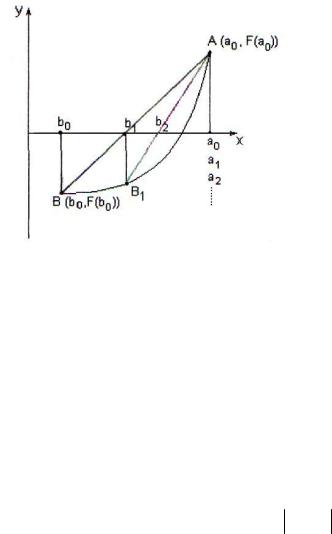
Рис. 3

Проведенная прямая пересекает ось ох

Найдем х при у=0

Далее, сравнивая знаки F(b1) и F(b0), найдем новый отрезок [b1, a0]. Соединим новой хордой точки А и В1, таким образом найдем новое приближение корня. Итерационный процесс продолжается до тех пор, пока F(bi) не станет по модулю меньше числа : F(bi ) . При решении этим методом потерять корень невозможно.

Рабочая формула метода хорд:

где b – начало отрезка, а – конец ( точка а неподвижна). Неподвижен тот конец, для которого знак функции F(x) совпадает

со знаком ее второй производной F (x).

Блок–схема алгоритма метода хорд представлена на рис. 4, где [a, b] – отрезок, в котором находится корень уравнения; b – корень уравнения; n – число итераций; F(bi) – значения функции в соответствующей точке.

2.3. Метод Ньютона (метод касательных)

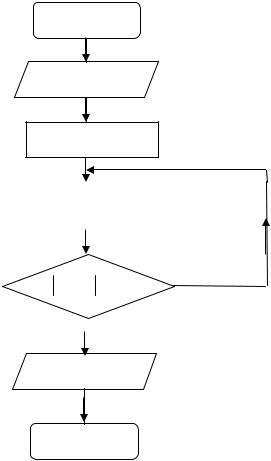
качестве начального приближения принимается тот конец отрезка [a, b], для которого выполняется условие F(x)F (x) 0. Обратимся к рис. 5, на котором представлено графическое решение задачи. Из точки А0 проведена касательная к функции. Точка пересечения касательной с осью ох является первым приближением корня, на рис. 5 она обозначена как а1. Затем из точки а1 проводим прямую, перпендикулярно оси ох. Точку пересечения этой прямой с функцией обозначим через А1 и т.д.

Начало

Ввод b,

i = 0

F(bi)

Нет

Вывод b, i

Конец

Рис. 4

Запишем уравнение прямой, касательной к F(x):

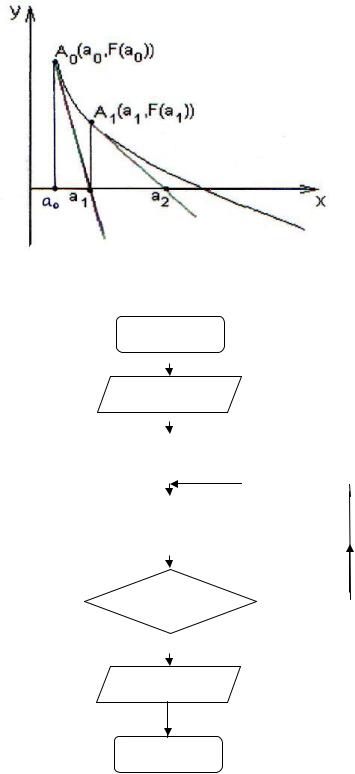
y F(a0) F (a0)(x a0).

Конец

Рис. 6

26

Рабочая формула метода касательных: ai 1 ai FF((aaii)),

ai 1 ai ai, i 0,1,2,3,...

Итерационный процесс продолжается до тех пор, пока F(x) не

тодом возможна потеря корня, но при правильном применении метода он сходится быстро, 4-5 итераций дают погрешность 10-5, он используется также для уточнения значения корня [5]. Блок-схема алгоритма метода касательных представлена на рис. 6, где an – корень уравнения; n – число итераций; F(an) - значение функции в соответствующей точке.

2.4. Комбинированный метод хорд и касательных

Задача. Найти корень уравнения F(x) с заданной точностью . В этом случае используется одновременно методы касательных и

хорд. Приближение к корню происходит с двух сторон. Рассмотрим четыре случая, которые отвечают возможным комбинациям знаков

F (x) и F (x).

Из графиков, представленных на рис. 7, метод хорд применяется со стороны вогнутости, а метод касательных – со стороны выпуклости графика.

Совместное применение обоих методов дает сразу избыточное и недостаточное приближение. Применяя этот метод, мы предполагаем,

что выпуклость кривой y F(x) при всех x [a0 , b0 ] обращена в одну сторону. Для удобства расчета обозначим через а0 тот конец отрезка [a0, b0], в котором знаки F (x) и F (x) совпадают.

Из возможных случаев рассмотрим случай первый. Пусть F(a)* F(b) 0 и F (x)* F (x) 0, т.е. знаки первой и второй производной совпадают. При решении уравнения каждая итерация заключается в следующем: из точки А проведем хорду, которая стягивает дугу АВ, и проведем касательную к дуге таким образом, чтобы точка пересечения касательной с осью ох оказалось внутри отрезка [a0, b0]. Хорда на графиках пересекает ось ох в точке b1,

27

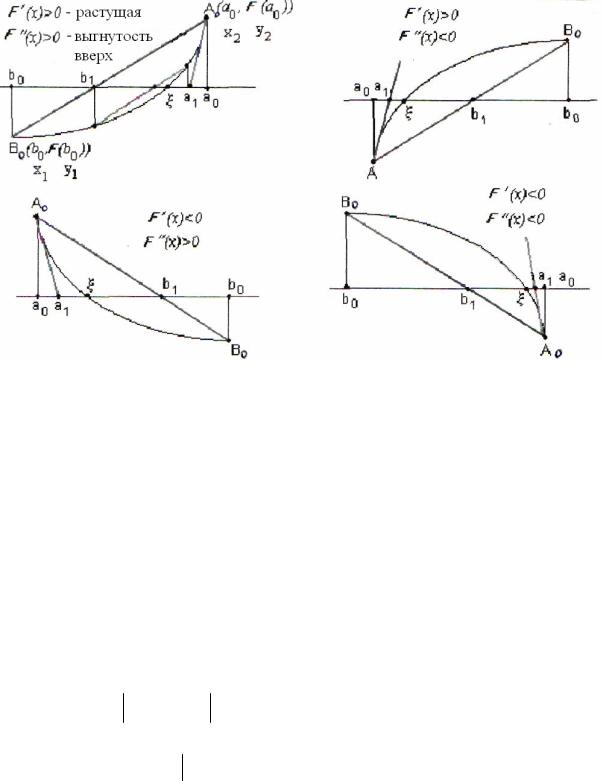
Рис. 7

лежащей между точками b0 и искомым корнем , а касательная к дуге в точке А пересекает ось ох в точке а0, лежащей между точками а0 и искомым корнем уравнения ( рис. 8).

Полученное значение a1 и b1 дают новое приближение к корню. Приведем расчетные формулы для ai+1и bi+1, выведенные в п.2.1 и 2.2.

Процесс нахождения ai+1 и bi+1 продолжается до тех пор, пока выполняется одно из следующих условий:

ai 1 bi 1 , где - заданная точность;

28

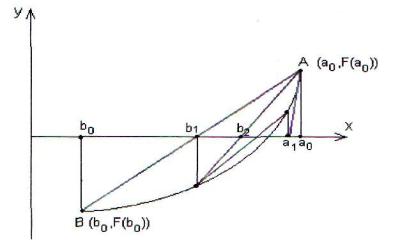
Рис. 8

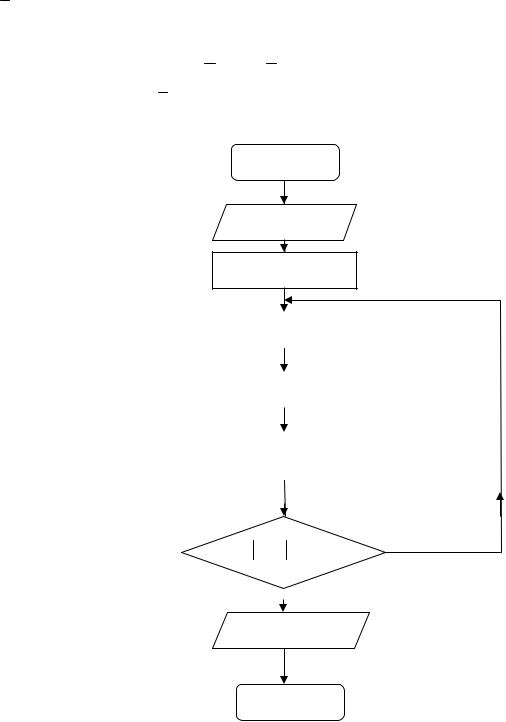
Все округления при вычислениях следует производить в сторону от корня [4]. На рис. 9 представлена блок-схема комбинированного метода хорд и касательных, где n число итераций; аn , b n− значения приближения корня; F(аn) F(bn) − значения функции в данных точках.

2.5. Метод простой итерации (метод последовательных приближений)

Чтобы применить метод простой итерации для решения нелинейного уравнения F(x)=0, необходимо преобразовать его к следующему

Это преобразование (приведение уравнения к виду, удобному для итерации) можно выполнить различными способами; некоторые из них будут рассмотрены ниже. Функция называется итерационной функцией.

Выберем каким-либо образом приближенное значение корня х(0) и подставим его в правую часть уравнения (2). Получим значение

х(1) (х(0) ). Подставим теперь х(1) в правую часть уравнения (2),

имеем х(2) (х(1) ). Продолжая этот процесс неограниченно, получим последовательность приближений к корню, вычисляемых по формуле

Если существует предел построенной последовательности

Начало

Ввод a, b,

i = 0

Нет

F(c)

Да Вывод c, i

Конец

Рис. 9

Метод допускает простую геометрическую интерпретацию. Построим графики функций у = x и у = (x), (рис. 10,а и 10,б). Корнем уравнения у = (x) является абсцисса точки пересечения кривой

30