Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1252

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

тижения заданной точности число слагаемых. Для этого оценим остаток ряда:

Rn			1						1						1				1
Rn		n 1! 2n 1					n 2 ! 2n 2						n 3 ! 2n 3					n 1! 2n 1
			1							1						1

												2								3
	1		n 2	2								2		n 2 n		3 n 4 2				3
			n 2	2	n 2 n 3 2									n 2 n		3 n 4 2
<			1			1		1			1				1			1				1	.
				1
	n 1! 2n 1			1							23				n 1! 2n 1				1		n 1! 2n
	n 1! 2n 1					2 22					23				n 1! 2n 1		1		1		n 1! 2n
																	1		2
																			2
	Путем подбора определим, при каком значении n будет выпол-

няться неравенство Rn 0,00001.

Полагаем, например, n 4, получа-

ем, что Rn 0,00026. При

n 5

Rn 0,0000022. При n 6

Rn 0,00000016<0,00001. Итак, принимаем n 6:

2! 22

3! 23

4! 24

5! 25

6! 26

1! 2

1,000000+0,500000+0,125000+0,020833+0,002604+0,000260+ +0,000022 1,648719.

Получили 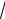e 1,648719. Каждое слагаемое вычисляли с точностью 0,000001, чтобы при суммировании не получить погрешности, превышающей 0,00001.

2. Вычислить	1	с точностью до 0,00001.

	6 e

Используем разложение в ряд функции ex. Имеем

1		1		1	1	1

	e 6		1				.
					2! 62	3! 63
6 e				1! 6

Данный ряд является виям признака Лейбница, лютной величине должна

знакочередующимся и удовлетворяет услопоэтому допускаемая погрешность по абсобыть меньше первого из отброшенных чле-

нов ряда. Так как						1			0,0000011 0,00001, то для вычисления ос-
							5! 65

тавляем только первые четыре слагаемые. Поэтому
1			1		1			1		1	1
		e	6 1									1,000000 0,166666

								2! 62		3! 63	4! 64
	6 e
				1! 6

+ 0,013888+0,000771 0,000032 0,847961 0,84796.

Все вычисления проводились с одним запасным знаком. Полученный результат округлили до пяти знаков после запятой.

3. Вычислить cos18o с точностью 0,0001. Используем разложение в ряд функции cos x. Имеем

cos18o cos		1	1	2	1			4		.

	10
	10		2! 10		4!		10
Ряд знакочередующийся, поэтому для достижения точности ис-
						1			6
пользуем признак Лейбница. Поскольку				a6						0,0001 , то
пользуем признак Лейбница. Поскольку				a6						0,0001 , то
						6! 10

достаточно взять три слагаемых ряда

cos18o 1 0,09870 0,00974 0,9511.

224

4.Вычислить 3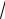130 с точностью до 0,001.

Найдем ближайшее к 130 число, которое является кубом целого числа. Это 125=53 . Сделаем преобразования :

			1	1
				1
3	130	3 53 5 5 3 1		51 0,04
					3
			25		3
			25

				1	1				1	2	5
		1					1
				3		3	1		3		3
5 1			0,04	3		3		0,0016	3	3	3	0,000064
5 1			0,04			2!		0,0016		3!		0,000064
	3					2!				3!

5 1 0,02 1 0,008 5 0,00032 . 3 9 8!

Четвертое слагаемое меньше 0,001, поэтому его и следующие за ним члены в сумме не превышают точности 0,001, их мы отбрасыва-

ем. Итак, 3130 5 0,0667 0,0009 5,066.

Отметим, что при решении было использовано разложение в ряд

функции 1 x 3 .

Упражнения. Вычислить приближенно с точностью :

1. sin	1	; 0,001;	2. ln1,04; 0,0001;

2

3.5 1,1;						0,0001;	4.	ln 2; 0,0001;
5.	sin 9o ; 0,0001;						6.	3		; 0,0001;
									1,06
7.					; 0,001;		8.	ch0,3; 0,0001;
		27
9.	1			;		0,000001;	10.	e; 0,00001.

			e

§8. Вычисление пределов и определенных интегралов с помощью рядов

При вычислении пределов и определенных интегралов иногда удобно разложить функции в степенные ряды. Покажем это на примерах.

Примеры.

1. Найти lim

sin x arctgx

x 0

Используем разложения в ряды по степеням x функций sin x и

arctgx. Получаем

sin x arctgx

lim

x 0

1 1

=lim

5 5!

x 0

2. Найти lim

2ex 2 2x x2

x sinx

x 0

Заменяем функции ex

и sin x на их разложения в ряды Маклоре-

на, получаем

2 2x x2

2 1 x

lim

2e 2 2x x

lim

x sinx

x 0

2x3

2x4

lim

x 0

Теперь рассмотрим примеры приближенного вычисления определенных интегралов.

Примеры.

0,3		dx
1. Вычислить интеграл			с точностью до 0,0001.

	3 1 x2
0,2	3 1 x2

Разложим подынтегральную функцию в степенной ряд, пользуясь биномиальным разложением:

					1		4	1		4	7
	1		1

1 x		1		x	3		3 x2	3		3	3 x3
	3
						2			6
		3

1 n 1 4 7 3n 2 xn , 1 x 1.

3n n!

Теперь подставим x2 вместо x, имеем

											1											1 4 7 3n 2

				1 x2								3 1								1 n						x2n , 1 x 1.
				1 x2								3 1								1 n						x2n , 1 x 1.
																		n 1						3n n!
			Воспользуемся возможностью почленного интегрирования сте-
пенного ряда:
0,3			dx



0,2 3 1 x2																								n 1 4 7 3n 2
	0,3				1			2		2					4		14				6			n 1 4 7 3n 2				2n
		1					x						x							x			1				x		dx
		1			3		x			9			x				27			x			1		3n n!		x		dx
	0,2				3					9							27								3n n!
				1		3			2					5			2			7				0,3
																								0,3

	x				x							x							x					0,1 0,00211 0,00009 0,09798
	x				x							x							x					0,1 0,00211 0,00009 0,09798
				9					45							81								0,2
				9					45							81								0,2

0,0980.

После почленного интегрирования получили знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница. Поскольку четвертый член ряда по модулю оказался меньше заданной точности 0,0001, то для вычислений мы взяли сумму первых трех слагаемых.

Отметим, что если после почленного интегрирования получится знакоположительный ряд, то для определения необходимого для вычислений числа слагаемых проводят оценку остатка ряда (обычно оценивают с помощью геометрической прогрессии).

2.Вычислить интеграл e x dx с точностью до 0,0001.

Разложим подынтегральную функцию в ряд, используя разложение в ряд Маклорена функции ex, заменяя x на x3. Получим

1	x	3				1			x3				x6			x9		x12		x15	x18
e	x		dx

					1				1!							3!		4!		5!	6!		dx
0						0			1!	2!						3!		4!		5!	6!
				x		4		x	7			x		10			x	13		16		x		19	1
																									1

x																				x
x
				4 1!			7 2!				10 3!					13 4!				16 5!	19 6!
				4 1!			7 2!				10 3!					13 4!				16 5!	19 6!				0
			1			1		1			1					1			1						0
1			1			1		1			1					1			1
1
		4			14		60			312					1920			13680

1 0,25 0,07142 0,01666 0,00320 0,00052 0,00007

0,80744 0,8074.

Поскольку мы использовали знакопеременный ряд, то для достижения точности вычислений необходимо было найти слагаемое

1 0,0001 и отбросить его и остальные члены ряда, так как воз13680

никающая при этом погрешность меньше, чем 0,00007. Вычисления проводили с пятью знаками после запятой.


2 sinx		dx с точностью до 0,5 10 3.
3. Вычислить интеграл
3. Вычислить интеграл	x
0	x

Заметим, что неопределенный интеграл sin x dx не берется в ко- x

нечном виде. Разложим sin x в ряд и деля почленно на x, получим

ряд sinx 1 x2 x4 x6 , сходящийся при любом значении x. x 3! 5! 7!

Интегрируя, получим

								x3		x5		x7		2

2 sinx
		dx

					x					5 5!
0	x						3 3!			5 5!		7 7!	0
				3				5			7		0
				3				5			7
			2			2				2
			2			2				2
									35280
2	18				600				35280
1,5708 0,2153 0,0159 0,0007 1,3707 1,371.
										9
Первый отброшенный член									2		много меньше, чем 0,5 10 3.
Первый отброшенный член											много меньше, чем 0,5 10 3.

9 9!

Упражнения.

Вычислить пределы:

1 cosx

sin

sinx

lim

;

2. lim

;

x 0 ex 1 x

x arctgx

e2x3

cosx3

lim

;

lim

2x3

x 0

Вычислить приближенно с точностью :

0,2 sin x

dx , 0,0001;

0,51 cosx

dx ,

0,0001;

0,1 ex 1

dx,

0,001;

0,1 ln 1 x

dx ,

0,001;

0,5

xln 1 x2 dx, 0,001;

10. e x

dx ,

0,001.

§9. Интегрирование дифференциальных уравнений с помощью рядов

В некоторых случаях, когда интегрирование дифференциального уравнения в элементарных функциях невозможно, решение такого

	x x0 n (метод не-
уравнения ищут в виде степенного ряда y an	x x0 n (метод не-
n 0

определенных коэффициентов). Неопределенные коэффициенты an , n 0,1,2, находят подстановкой ряда в уравнение и приравнивая коэффициенты при одинаковых степенях разности x x0 в обеих частях полученного равенства. Если удается найти все коэффициенты ряда, то полученный ряд определяет решение на всей области сходимости.

В тех случаях, когда для уравнения y f x,y требуется решить задачу Коши при начальном условии y x x0 y0 , решение можно ис-

	y	n	x0		x x	n , где y x		y
кать с помошью ряда Тейлора y							0		0	;

n 0		n!		0

y x0 f x0 ,y0 , а дальнейшие производные y n x0 находят последовательным дифференцированием исходного уравнения и подста-

новкой в результат дифференцирования предварительно вычисленных приx x0 значений производных до порядка n 1 (метод последовательного дифференцирования). Аналогично с помощью ряда Тейлора можно интегрировать и уравнения высших порядков.

Примеры.

1. Методом неопределенных коэффициентов найти общее решение линейного дифференциального уравнения

4x2 1 y 8xy 8y e x2 16x4 4x2 10

в виде ряда по степеням x.

Решение уравнения будем искать в виде ряда по степеням x: y a0 a1x a2x2 anxn .

Тогда

y a1 2a2x 3a3x2 nan 1xn ;

y 2a2 6a3x 12a4x2 n n 1 anxn 2 .

Разложим в ряд правую часть уравнения, используя разложение в ряд функции ex, получим

x2	16x	4		2	10 16x	4		2		2 x4		n x2n

e			4x				4x			1 x		1		.
e			4x				4x		10	1 x		1		.
											2		n!
											2		n!

Теперь все найденные разложения подставляем в исходное уравнение, получаем

4x2 1 2a2 6a3x 12a4x2 n n 1 anxn 2

8x a1 2a2x 3a3x2 nanxn 1

8 a0 a1x a2x2 anxn

16x	4		2			2 x4	n x2n

		4x			1 x		1		.
		4x		10	1 x		1		.
						2		n!
						2		n!

Приравниваем коэффициенты при одинаковых степенях x в левой и правой частях равенства, получаем

2a2

8a0 10;

6a 8a 8a 0;

8a2 12a4 16a2 8a2

4 10;

4 2n 2n 1 a2n 2n 2 2n 1 a2n 2 8 2na2n 8a2n

1 n 16

1 n 1 4

1 n 10

при четных степенях ;

n 1!

n 2 !

4 2n 1 2na

2n 1

2n 3 2n 2 a

2n 3

8 2n 1 a

2n 1

при нечетныхстепенях .

Решая систему, получаем рекуррентные соотношения для четных и нечетных коэффициентов:

a2 4a0 5;

a3 0;

1a4 2;

4 n 1 2n 1

n 1

2 10n 5

,n 2

;

2n 2

n 1 2n 1

n! n 1 2n 1

4n 2n 1

2n 3

2n 1

,n 1.

n 1 2n 3

Эти соотношения позволяют любой коэффициент ряда выразить через первые два коэффициента a0 и a1, которые играют роль произвольных постоянных в общем решении дифференциального уравнения второго порядка. Легко понять, что все нечетные коэффициенты равны нулю, поскольку a3 0. Для четных коэффициентов последовательно получаем


a6			4		a4		17			2			17				1			1	;
							30
	5									5		30				6			3!
a		10				a			47						10			47				1		1		;
									6 4 7
8	7					6									42 42 4 24 4!
a				4 3 7				a				93							84				93					1		1	;
											24 5												24 5		9
10					5 9		8							9		24 5 9											120		5!

…

a2n 1 n			1	, n 2.
a2n 1 n				, n 2.
			n!
Итак, общее решение уравнения запишется в виде
y a	0	a x 4a			0	5 x2		1	x4		1	x6		1	x8	1	x10 .
y a		a x 4a				5 x2			x4			x6			x8		x10 .
		1					2			6			24		120
							2			6			24		120

Сгруппируем члены следующим образом:

		1 4x	2 a x 5x2	1	x4		1	x6 1 n 1	x	2n 2
y a	0

			1	2		6			n 1!

Проанализируем структуру общего решения. Из теории дифференциальных уравнений известно, что общее решение линейного неоднородного уравнения представляет собой сумму общего решения соответствующего однородного уравнения y a0 y1 a1y2 и частного решения y* неоднородного уравнения, то есть y y y*. При этом y1, y2 есть фундаментальная система решений соответствующего однородного уравнения. В полученном общем решении данного диффе-


ренциального уравнения y 1 4x2 ;					y	2	x− фундаментальная сис-
			1			2					1 4x2 a x
тема решений однородного линейного уравнения,								y	a	0	1 4x2 a x
− общее решение однородного линейного уравнения,										0	1
− общее решение однородного линейного уравнения,
	1 n	x	2n
y* 5x2		x		− частное решение данного уравнения. Заме-
y* 5x2				− частное решение данного уравнения. Заме-
n 2		n!

тим, что y* e x2 4x2 1, поэтому общее решение данного уравнения можно записать в виде

ya0 1 4x2 a1x e x2 4x2 1.

2.Найти первые 4−5 членов разложения в ряд Тейлора частного

решения дифференциального уравнения y ey x2 при начальном условии y x 1 0 (метод последовательного дифференцирования).

Так как начальное условие задано при x 1, то решение уравнения будем искать в виде ряда Тейлора по степеням x 1:

y x y 1 y 1 x 1 y 1 x 1 2 y n 1 x 1 n .

2! n!

Из начального условия известно, что y 1 0. Подставим в данное уравнение x 1; y 0, найдем, что y 1 2. Для нахождения y 1 продифференцируем обе части исходного уравнения, используя правило дифференцирования сложной функции: y ey y 2x и

подставим в полученное равенство x 1; y 0; y 1 2. Получим y 1 4. Продолжаем описанную процедуру, получаем

y ey y 2 ey y 2, y 1 10; y IV ey y 3 3y y y , y IV 1 42

и т.д.

Теперь решение данного уравнения можно записать в виде

y x 2 x 1 2 x 1 2 5 x 1 3 7 x 1 4 .

3 4

Следует отметить, что метод последовательного дифференцирования, являясь очень простым, имеет существенные недостатки, а именно: общий член ряда найти практически невозможно, поэтому нельзя установить интервал сходимости ряда. Первые члены ряда дают возможность находить приближенно значения уравнения для x, близких к единице. При этом ошибка приближения остается неизвестной.

3. Найти первые пять членов разложения в ряд решения задачи Коши:

y 2x 1 y 1;y 0 0;

y 0 1.

Поскольку начальные условия заданы при x 0, используем формулу Тейлора по степеням x(формулу Макорена):

y 0 x

y x y 0 y 0 x

Из условия задачи известны y 0 и

y 0 . Подставим x 0; y 0

в данное дифференциальное уравнение, получим y

0 1. Теперь

продифференцируем уравнение: y 2y 2x 1 y .

Используем ра-

нее найденные данные

x 0; y 0; y 0 1.

Получим

y 0 1.

Продолжаем дифференцирование:

y IV 2y 2y 2x 1 y , y IV 0 5; y V 4y 2y 2x 1 y , y V 0 5; y VI 6y 2y 2x 1 y IV , y VI 0 13.

Теперь запишем вид получившегося разложения:

y x x	x2		x3	5x4		5x5		13x6	.

2!		3! 4!			5!		6!

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021996.83 Кб21248.pdf
#
07.01.2021997.2 Кб11249.pdf
#
07.01.2021300.65 Кб0125.pdf
#
07.01.20211 Mб01250.pdf
#
07.01.20211 Mб11251.pdf
#
07.01.20211 Mб01252.pdf
#
07.01.20211 Mб11253.pdf
#
07.01.20211 Mб11254.pdf
#
07.01.20211.01 Mб21255.pdf
#
07.01.20211.01 Mб71256.pdf
#
07.01.20211.01 Mб11257.pdf