
Физика_лек_pdf / Модуль 1. Физические основы механики
.pdf
Если материальная точка движется прямолинейно, то модуль момента импульса равен L = mvl , при движении материальной точки по окружности радиусом R момент импульса относительно центра окружности равен L = mvR .
Момент импульса твердого тела относительно оси z представляет собой сумму моментов импульса отдельных частиц
Используя формулу vi = ωri , получим  , то есть
, то есть
Lz = Jz ω , Дж · с. (3.6)
Следует обратить внимание на то, что у ω индекс не ставится, так как эта величина одинакова для всех точек тела.
Итак, момент импульса твердого тела относительно оси z равен произведению момента инерции тела относительно той же оси на его угловую скорость.
Продифференцируем уравнение (3.6) по времени
Момент силы относительно оси z может быть преобразован к виду:
Таким образом, dL / dt = Mz . Наряду с изложенным, имеет место векторное равенство  .
.
В изолированной системе момент внешних сил отсутствует, то есть  и
и  , а следовательно, момент импульса изолированной системы остается постоянным:
, а следовательно, момент импульса изолированной системы остается постоянным:  .
.
Подобно законам сохранения энергии и импульса, закон сохранения момента импульса принадлежит к числу фундаментальных законов природы. Моментом импульса обладают не только движущиеся макроскопические системы, но и отдельные элементарные частицы, а также атомные ядра, атомы, их ассоциативные комплексы. Причем некоторые элементарные частицы и их системы могут иметь моменты импульса, не связанные с движением в пространстве, и называют их спинами.
В справедливости закона сохранения момента импульса можно убедиться на опыте с уравновешенным гироскопом. Он предоставляет собой вращающееся симметричное твердое тело, ось вращения которого способна изменять свое направление в пространстве относительно некоторой неподвижной точки, называемой центром подвеса. Если центр
подвеса совпадает с центром тяжести гироскопа, то результирующий момент сил тяжести всех частей по отношению к центру подвеса равен нулю. Такой гироскоп называют
уравновешенным. Так как гироскоп симметричен, то его момент импульса  направлен вдоль основной оси вращения, проходящей через диск. Поэтому при любом положении гироскопа ориентация его основной оси вращения остается неизменной.
направлен вдоль основной оси вращения, проходящей через диск. Поэтому при любом положении гироскопа ориентация его основной оси вращения остается неизменной.
Справедливость закона сохранения момента импульса подтверждается опытом со скамьей Жуковского. Горизонтальная круглая скамья вращается без трения. На ней стоит человек и держит в вытянутых руках гантели — ( J 0 + 2 mr 1 2 )ω1 = const , где J 0 — момент инерции человека и скамьи; m — масса одной гантели. Приближая гантели к груди, человек уменьшает момент инерции всей системы, а угловая скорость ее вращения должна при этом возрастать — ( J + 2 mr 2 2 )ω2 = ( J 0 + 2 mr 1 2 )ω1 , где 2 mr 1 2 и 2 mr 2 2 — моменты инерции гантелей в первом и втором положениях относительно оси вращения; r 1 и r 2 , — расстояния от гантелей до оси вращения; ω1 и ω2 угловые скорости вращения системы соответственно в состояниях 1 и 2.
Вращающаяся с большой скоростью масса сохраняет неизменной ось своего вращения, то есть сохраняет вектор момента импульса. Этим обусловлена устойчивость положения земной оси, продольной оси летящего снаряда, пули, вертикальная устойчивость движущегося велосипеда.
Основной закон динамики вращательного движения твердого тела. Кинетическая энергия вращающегося тела
Из равенства М z = Jz d ω / dt с учетом того, что d ω / dt представляет собой угловое ускорение, следует основной закон динамики вращательного движения твердого тела относительно неподвижной оси
М z = Jz ε , H · м.
Очевидно, что угловое ускорение, сообщаемое телу моментом силы, тем больше, чем меньше момент инерции, то есть момент инерции характеризует инерционные свойства тела при вращательном движении. Но в отличие от массы, момент инерции конкретного тела может иметь множество значений соответственно множеству возможных осей вращения.
Кинетическая энергия одной частицы массой т 1 вращающегося тела, движущейся со скоростью v 1 по окружности радиусом r 1 , равна:
E к i = mi vi 2 /2 = mi ri 2 ω2 /2 = Ji ω2 /2, Дж,
где Ji — момент инерции материальной точки; ω — угловая скорость вращения тела. Суммируя энергии E к i всех материальных точек, получим формулу для кинетической энергии тела, вращающегося вокруг неподвижной оси z :
E к = Jz ω2 /2, Дж,
В технике для равномерного хода прокатных станов, кораблей, тракторов и других машин широко используют маховое колесо, аккумулирующее кинетическую энергию вращения вала. К сведению, скорость вращения композитных роторных устройств (маховиков в том числе) достигает 600 тыс. оборотов в минуту. Это чрезвычайно высокая скорость. Прочность, необходимая при этом, обеспечена композитом.

Если тело одновременно участвует в поступательном и вращательном движениях, то его кинетическая энергия определяется следующим образом:
E к = mv 2 /2 + Jz ω2 /2, Дж,
Работа вращающего момента силы, приложенной к телу, равна изменению кинетической энергии тела
А = Jz ω2 2 /2 – Jz ω1 2 /2, Дж.
Каждой физической величине, характеризующей поступательное движение, соответствует определенная физическая величина, характеризующая вращательное движение. Эта аналогия наблюдается и при сравнении законов поступательного и вращательного движений. Однако в математических выражениях для вращательного движения вместо силы присутствует ее момент, а роль массы выполняет момент инерции, аналогом же импульса тела является момент импульса тела. Сказанное для наглядности представлено в табл. 3.1.
Таблица 3.1
Основные физические величины и формулы для поступательного и вращательного движений
Цит. по: Физика: учебник / Демидченко В.И. — Ростов н/Д: Феникс, 2006. — С. 46–51.
Момент инерции

Момент инерции — это мера инертности вращающегося тела.
Момент инерции материальной точки относительно оси вращения: 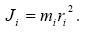 .
.
Момент инерции системы материальных точек относительно оси вращения:
Если тело сплошное, то сумму заменим интегралом по dm и представим dm = pdV :
Момент инерции J — скалярная величина, зависит от массы и ее распределения относительно оси вращения. Зависит от формы тела. Легко найти для тел правильной геометрической формы.
Примеры расчета моментов инерции различных тел.
Пример 1. Момент инерции однородного обруча радиуса R , массы m .
Разобьем обруч на элементарные массы mi . Расстояние от оси вращения до любой элементарной массы равно радиусу обруча: ri = R .
Пример 2. Момент инерции однородного цилиндра массы m , радиуса R
относительно его геометрической оси.

Разобьем цилиндр на слои радиуса r , толщины dr . Масса такого тонкого слоя 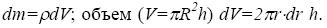 Тогда
Тогда 
Все точки слоя отстоят от оси ОО1 на одинаковом расстоянии r .
Момент инерции цилиндра не зависит от его высоты h . Тогда и для диска момент инерции относительно оси, перпендикулярной диску, проходящей через его центр масс:
Пример 3. Момент инерции стержня массы m , длины l относительно оси, проходящей через центр масс ОО .
Масса |
стержня, |
приходящаяся |
на единицу длины |
Для |
элемента длины dx , |
масса |
|
|
|

Пример 4. Момент инерции стержня, массы m , длины l относительно
перпендикулярной ему оси, проходящей через его конец.
Рассуждения аналогичные предыдущему примеру.
Анализируя примеры 3 и 4, приходим к выводу: момент инерции тела зависит от выбора оси вращения. Момент инерции относительно произвольной оси можно вычислить, применяя теорему Штейнера.
Теорема Штейнера: Момент инерции тела относительно произвольной оси равен сумме J 0 момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
Пример 5. Рассмотрим пример 4 с применением теоремы Штейнера:
Вычисление оказалось гораздо проще и быстрее.

Цит. по: Конспект лекций по дисциплине «Физика» для студентов технических специальностей заочной формы обучения. Ч. 1 / Сост. В.А. Сарафанова / — Тольятти: ТГУ, 2008. — С. 25–27.
Тема 4. Тяготение
Законы Кеплера и Закон всемирного тяготения
1. В результате длительной обработки многолетних наблюдений датского астронома Тихо Браге (1546–1601) немецкий ученый Кеплер эмпирически установил три закона движений планет. Эти законы формулируются следующие образом:
1)каждая планета движется по эллипсу, в одном из фокусов которого находится
Солнце;
2)радиус-вектор планеты в равные времена описывает равные площади;
3)квадраты времен обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг Солнца.
Первые два закона были опубликованы Кеплером в 1609 г., последний — в 1619 г. Законы Кеплера естественным путем привели Ньютона к открытию закона всемирного тяготения. Рассмотрим этот вопрос.
Из первого закона Кеплера следует, что траектория планеты — плоская кривая. С учетом этого обстоятельства из второго закона Кеплера следует, что сила, заставляющая планету двигаться по замкнутым орбитам, направлена к Солнцу. Определим теперь, как эта сила изменяется с изменением расстояния от Солнца и как она зависит от массы планеты. Для упрощения расчетов допустим сначала, что планета движется не по эллипсу, а по кругу, в центре которого находится Солнце. Для планет Солнечной системы такое допущение не является особенно грубым. Эллипсы, по которым на самом деле движутся планеты, весьма мало отличаются от кругов. Ускорение планеты при равномерном движении по круговой орбите радиуса r выражается формулой

Для планет, движущихся по круговым траекториям, третий закон Кеплера записывается в виде
или
где К — постоянная для всех планет Солнечной системы. Она называется постоянной Кеплера . Через параметры эллиптической орбиты постоянная Кеплера выражается формулой
где а — длина большой полуоси орбиты.
Выразив Т через К и r , для ускорения планеты при движении по круговой орбите получим
Сила, действующая на планету, равна
где m — масса планеты.
Мы доказали, что ускорения двух разных планет, обращающихся вокруг Солнца по круговым орбитам, обратно пропорциональны квадратам расстояний их от Солнца. Но мы еще не доказали, что такая закономерность справедлива и для одной и той же планеты, обращающейся вокруг Солнца по эллиптической орбите. Чтобы доказать это, надо от рассмотрения круговых движений перейти к исследованию движений по эллипсу. Это будет сделано в следующем параграфе. Но можно обойтись и круговыми движениями, если использовать добавочное предположение, что сила взаимодействия между Солнцем и планетой зависит только от мгновенного расстояния между ними, но не зависит от формы траектории, по которой движется планета. Тогда формулы (5.2) и (5.3) можно применять не только к разным планетам, обращающимся по круговым орбитам на разных расстояниях от Солнца, но и к различным положениям одной и той же планеты, движущейся по эллиптической траектории.
2. Коэффициент пропорциональности 4π2 К , входящий в формулы (5.2) и (5.3), — один и тот же для всех планет, а потому он не может зависеть от массы планеты. Он

может, однако, зависеть от параметров, характеризующих Солнце, поскольку последнее является источником сил, заставляющих планеты двигаться по замкнутым орбитам. Но Солнце и планета в их взаимодействии выступают как равноправные тела . Различие между ними только количественное . Они отличаются друг от друга массами. И если сила взаимодействия F пропорциональна массе планеты m , то она должна быть пропорциональна также и массе Солнца М . Для этой силы можно поэтому написать
где G — новая постоянная, уже не зависящая ни от массы Солнца, ни от массы планеты. Сравнивая эту формулу с (5.3), получаем следующее выражение для постоянной Кеплера:
3. Далее, Солнце и планеты отличаются друг от друга и от других тел только количественно — значениями масс. Поэтому естественно предположить, что притяжение существует не только между Солнцем и планетой, но и между планетами, а также между любыми другими телами, и что сила притяжения определяется формулой (5.4), в которой под М и m следует понимать массы взаимодействующих тел. Это предположение было введено Ньютоном и подтвердилось на опыте. Он сформулировал закон всемирного тяготения, согласно которому любые два тела (материальные точки) притягиваются друг к другу с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними . Такие силы называются гравитационными или силами всемирного тяготения . Коэффициент пропорциональности
G , входящий в формулу (5.4), один и тот же для всех тел. В этом смысле он является универсальной постоянной. Это одна из важнейших мировых постоянных, называемая
гравитационной постоянной .
В приведенной формулировке закона всемирного тяготения предполагается, что взаимодействующие тела являются точечными . Физически это означает, что размеры тел очень малы по сравнению с расстоянием между ними. Здесь, как и всегда в физике, слова «велик» и «мал» употребляются в относительном смысле — велик или мал по сравнению с чем-то . Указанное условие хорошо выполняется для взаимодействий Солнца с планетами, планет между собой и со спутниками. Но если речь идет о гравитационном притяжении двух тел с размерами 10 см, когда расстояние между их центрами масс составляет, например, 20 см, то такие тела не могут рассматриваться как точечные. Чтобы рассчитать их гравитационное взаимодействие, надо мысленно разбить каждое тело на очень малые части, подсчитать по формуле (5.4) силы притяжения между такими частями, а затем и эти силы геометрически сложить (проинтегрировать). В основе этого вычисления лежит принцип суперпозиции гравитационных полей . Согласно этому принципу гравитационное поле, возбуждаемое какой-либо массой, совершенно не зависит от наличия других масс . Кроме того, гравитационное поле, создаваемое несколькими телами, равно геометрической сумме гравитационных полей, возбуждаемых этими телами в отдельности . Принцип этот является обобщением опыта.
Пользуясь принципом суперпозиции легко доказать, что два однородных шара притягиваются между собой так, как если бы их массы были сконцентрированы в их центрах .

Заметим еще, что каждая планета подвергается гравитационному притяжению не только Солнца, но и других тел Солнечной системы. Однако масса Солнца является преобладающей. Она более чем в 700 раз превосходит общую массу планет и всех остальных тел Солнечной системы. Благодаря этому Солнце является основным телом, управляющим движением планет. Законы Кеплера можно вывести из закона всемирного тяготения Ньютона . При таком выводе предполагается, что единственной силой, действующей на планету, является гравитационное притяжение Солнца. Поэтому законы Кеплера являются приближенными законами , не учитывающими гравитационное действие остальных тел Солнечной системы.
4. Во времена Ньютона закон всемирного тяготения был подтвержден только астрономическими наблюдениями над движениями планет и их спутников. Впервые непосредственное экспериментальное доказательство этого закона для земных тел, а также численное определение гравитационной постоянной G были даны английским физиком Г. Кавендишем (1731–1810) в 1798 г. Прибор Кавендиша состоял из легкого горизонтального коромысла (рис. 171а ), на концах которого укреплялись два одинаковых свинцовых шарика массой m . Коромысло подвешивалось на тонкой вертикальной нити а b . Вблизи свинцовых шариков массой m помещались два других больших свинцовых шара с массой М каждый, причем М >> m . Шары помещались сначала в положении AA , затем переводились в положение ВВ (рис. 171б ). Благодаря гравитационному взаимодействию шариков т с шарами М коромысло поворачивалось из положения равновесия. Угол кручения α измерялся наблюдением луча света, отражавшегося от зеркальца S . Если r — расстояние между центрами малого и большого шаров, а l — длина коромысла, то момент пары гравитационных сил, поворачивающих коромысло, будет
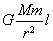 . В положении равновесия этот вращающий момент должен быть уравновешен упругим моментом закрученной нити f α. Написав условие равновесия для положения свинцовых шаров сначала в AA (α = α1 ), а затем в ВВ (α = α2 ), получим два уравнения
. В положении равновесия этот вращающий момент должен быть уравновешен упругим моментом закрученной нити f α. Написав условие равновесия для положения свинцовых шаров сначала в AA (α = α1 ), а затем в ВВ (α = α2 ), получим два уравнения
Рис. 171
Из них находим
Модуль кручения f легко найти, наблюдая период свободных колебаний коромысла
