Физика_лек_pdf / Модуль 5. Электростатика. Постоянный ток

проводника перпендикулярны его поверхности. Деформация однородного электрического поля, вызываемая незаряженным проводником круглого сечения, представлена на рис. 9.16. Таким образом, внесенный в электрическое поле проводник вызывает искажение этого поля. Вблизи проводника внешнее поле становится неоднородным.

Рис. 9.16

Индуцированные заряды в состоянии равновесия, когда внешнее поле внутри проводника скомпенсировано собственным полем индуцированных зарядов, располагаются на поверхности проводника. Можно утверждать, что физическая сущность явления электростатической индукции состоит в экранировании электрических полей. При этом экранирование распространяется на все пространство, ограниченное поверхностью проводника. На этом свойстве проводников основана электростатическая защита чувствительных приборов и различных устройств. Устройство, которое необходимо защитить от внешнего электрического поля, окружают со всех сторон проводником, например в виде металлической сетки, соединенной с землей. Потенциал экрана относительно Земли в любом поле равен нулю. Поле внутри его полости отсутствует. На экране может возникнуть индуцированный заряд только одного знака, а заряд противоположного знака уйдет в Землю.

Явление электрической индукции имеет место и в проводящих растворах кислот, солей и щелочей. Однако в этих средах указанное явление сопровождается перемещением положительных и отрицательных ионов.

И еще: для тушения пожара будет израсходовано намного меньше воды, если ее

электростатически зарядить на выходе из брандспойта. Образующиеся в этом случае капельки станут меньше; они будут буквально притягиваться к пламени.

Электроемкость. Конденсаторы

Экспериментом установлено, что проводник, удаленный от других проводников или тел, или, зарядов, при сообщении ему некоторого заряда q приобретает потенциал θ. Происходит это в результате взаимодействия зарядов, распределенных по поверхности этого проводника. При изменении заряда проводника будет меняться и его потенциал. Но, как показывают опыты, отношение заряда проводника к его потенциалу при неизменных внешних условиях остается постоянным: q / θ = const . Следовательно, между зарядом проводника и его потенциалом имеет место прямо пропорциональная зависимость. Вводя

Систему двух проводников, разделенных слоем диэлектрика, называют конденсатором. Обкладки конденсатора имеют одинаковый по величине, но противоположный по знаку заряд. Конденсаторы способны при незначительных размерах накапливать значительные по величине заряды. Они обладают большой электроемкостью при небольших относительно окружающих тел потенциалах. В зависимости от формы обкладок различают плоские, сферические, коаксиальные цилиндрические и другие конденсаторы. В конденсаторах всех типов поле, создаваемое накопленными зарядами, сосредоточено в узком зазоре между обкладками конденсатора. В этом случае окружающие тела не влияют на электроемкость конденсатора. В зависимости от вида диэлектрика конденсаторы бывают воздушными, бумажными, слюдяными, керамическими, электролитическими и др.

Рис. 9.19

Наиболее простым является плоский конденсатор (рис. 9.19). Для такого конденсатора с поверхностной плотностью зарядов ζ на пластинах площадью s каждая, разделенных диэлектриком толщиной d и диэлектрической проницаемостью ε, напряженность поля равна градиенту потенциала:

E = – grad θ = – Δθ / n = – Δθ / d = ( θ 1 – θ 2 ) / d .

Откуда θ1 – θ2 = Ed . Но так как согласно формуле (9.11) напряженность конденсатора Е = ζ/(ε0 ε),то θ 1 – θ 2 = [ ζ / (ε0 ε)] d = ζd / (ε0 ε). Принимая во внимание, что q = ζS , получаем формулу электроемкости плоского конденсатора:

С = q / ( θ 1 – θ 2 ) = ζs / [ ζd / (ε0 ε)] = ε0 ε s / d , Ф. (9.17)

Очевидно, что электроемкость плоского конденсатора прямо пропорциональна площади пластины и диэлектрической проницаемости среды, разделяющей пластины и обратно пропорциональна расстоянию между пластинами.

Для получения нужной электроемкости конденсаторы соединяют друг с другом параллельно, последовательно или смешанно. При параллельном соединении {рис. 9.20) суммарный заряд: q = q 1 + q 2 + q 3 ; суммарная электроемкость: С = С 1 + С 2 + С3 ; разность потенциалов: θ 1 – θ 2 = U 1 = U 2 = U 3 , где U 1 , U 2 , U 3 — напряжение между обкладками соответствующего конденсатора. При последовательном соединении те же

суммарные характеристики соответственно равны q 1 = q 2 = q 3 ; 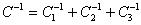и θ

1 – θ 4 = U 1 + U 2 + U 3 .

Рис. 9.20

Разность потенциалов между пластинами конденсатора, при которой происходит электрический разряд через слой диэлектрика, называют пробивным напряжением. Это одна из характеристик конденсаторов.

Бумажные конденсаторы применяются для напряжений в несколько сот вольт и имеют емкость в несколько микрофарад. В таких конденсаторах обкладками служат две длинные ленты тонкой металлической фольги, а изолирующей прокладкой между ними — несколько более широкая бумажная лента, пропитанная парафином. Такой же бумажной лентой покрывается одна из обкладок. Затем ленты туго сворачиваются в рулон, и последний укладывается в корпус.

Врадиотехнике применяются плоские конденсаторы небольшой электроемкости до 5·103 пФ. В них листки станиоля перекладываются также парафинированной бумагой или слюдой таким образом, что четные листы станиоля объединены и образуют одну обкладку конденсатора, а соединенные нечетные листки — другую.

Вмощных генераторах электрических колебаний высокой частоты применяются керамические конденсаторы малой электроемкости горшечного типа. Функции пластин конденсатора в них выполняют металлизированные внутренняя и внешняя поверхности керамического диэлектрика.

Вэлектролитических конденсаторах диэлектриком является тончайший слой окислов алюминия. И поэтому при малых размерах они обладают значительной электроемкостью, достигающей десятков и сотен мкФ.

Энергия заряженного проводника. Энергия конденсатора. Энергия электрического поля

Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник. Работа направлена против кулоновских сил отталкивания между одноименными зарядами и идет на увеличение электрической энергии dW заряженного проводника. При бесконечно малом увеличении заряда проводника на dq : dA = – dW = θdq = – C θd θ . Чтобы зарядить проводник от нулевого потенциала до θ,

необходимо совершить работу , Дж. Полученное равенство справедливо для электрического поля любой конфигурации.

Конденсатор, как и всякий заряженный проводник, обладает электрической энергией,

равной W = C (– Δθ )2 / 2 = q ( – Δθ ) / 2 = q 2 / (2 C ), Дж. Но так как θ1 – θ2 = Ed , а С = ε0 ε s / d , то W = [[0,5 ε 0 εs / d ]] E 2 d 2 = 0, 5 ε 0 εE 2 sd , Дж. А с учетом того, что объем

конденсатора равен sd = V , м3 , получим:

W = 0,5ε0 εE 2 V , Дж. (9.18)

Поскольку в полученной формуле присутствует объем между пластинами конденсатора, то можно сделать вывод о том, что энергия конденсатора сосредоточена не на обкладках, а в пространстве между ними. Если же коснуться истории развития этого вопроса, то следует вспомнить следующее. Вначале, когда была признанной теория дальнодействия, полагали, что энергия сконцентрирована на металлических пластинах конденсатора, поскольку на них находятся электрические заряды. Затем М. Фарадеем и Дж. Максвеллом была разработана теория близкодействия, согласно которой считали, что электрическая энергия связана с особым напряженным состоянием материальной среды

— поля, где проявляются электрические силы. Согласно этой точке зрения, энергия конденсатора рассредоточена в среде между пластинами конденсатора.

Независимо от характера распределения зарядов в пространстве напряженность электрического поля указывает на некоторое особое состояние среды, заполняющей это пространство. Это особое состояние среды определяет понятие электрического поля, в объеме которого сосредоточено тем больше электрической энергии, чем больше напряженность и объем поля. В связи с изложенным и поскольку все электрическое поле находится внутри конденсатора, можно считать, что формула (9.18) выражает не только энергию электрического поля конденсатора, но и энергию электрического поля вообще. Энергия электрического поля пропорциональна квадрату его напряженности и объему охваченного им пространства.

Плотностью энергии электрического поля называют отношение энергии электрического поля к занимаемому им объему

w = W / V = ε 0 εE 2 / 2, Дж/м3 .

В электрической форме не удается запасти большое количество энергии. Например в 1 м3 конденсатора при технически осуществимом значении Е = 107 В/м — всего 440 Дж. Однако эта энергия играет значительную роль при включении конденсаторов в цепь переменного тока, когда происходит их перезарядка с высокой частотой.

Цит. по: Физика: учебник / Демидченко В.И. — Ростов н/Д: Феникс, 2006. — С. 212–241.

Тема 2. Постоянный электрический ток

Электрический ток. Сила тока. Плотность тока

Электрическим током называют направленное движение электрических зарядов. Для возникновения и существования электрического тока необходимо наличие свободных электрически заряженных частиц и электрического поля, за счет энергии которого осуществлялось бы упорядоченное движение зарядов и энергия которого постоянно восполнялась бы. За направление тока условно принимают направление движения положительных зарядов. Электрический ток в проводнике называют током проводимости. В проводнике под действием приложенного электрического поля, заданного вектором

напряженности , перемещение положительных зарядов происходит вдоль поля, а отрицательных — против поля.

Рис. 10.1

Количественной мерой электрического тока является сила тока I , А. В общем случае сила тока равна первой производной по времени от заряда, проходящего через поперечное сечение проводника, I = dq / dt , А. Ток, сила и направление которого не меняются со временем, называют постоянным: I = q / t , A .

Плотностью тока называют отношение силы тока к площади поперечного сечения проводника, перпендикулярной направлению тока j = dI / ds , А/м2 .

Закон Ома для участка цепи. Электрическое сопротивление. Сверхпроводимость

Закон Ома для участка цепи отражает тот факт, что сила тока в проводнике, в котором отсутствует источник тока, прямо пропорциональна напряжению, приложенному на концах данного проводника, и обратно пропорциональна его сопротивлению:

I = U / R , A . (10.1)

Здесь: R — электрическое сопротивление проводника, Ом. Оно характеризует способность проводника препятствовать направленному движению заряженных частиц. Проводник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем 1 А. Для однородного линейного проводника величина электрического сопротивления прямо пропорциональна длине l и обратно пропорциональна площади поперечного сечения s проводника:

где ρ — удельное электрическое сопротивление, Ом·м. Это индивидуальная характеристика проводника, представляющая собой сопротивление проводника длиной 1 м с площадью поперечного сечения 1 м2 . Наименьшим удельным сопротивлением обладают серебро ρ = 1,6·10–8 , медь — 1,7·10–8 и алюминий — 2,6·10–8 Ом·м. Следует обратить внимание на то, что алюминий в сравнении с медью, обладает меньшей плотностью и прочностью на излом.

Удельное электрическое сопротивление проводника обусловлено электронэлектронным, электрон-фононным и другими взаимодействиями. Эти взаимодействия, и особенно электрон-фононное, приводят к потере электрической энергии. Величина потерь пропорциональна «удельному сопротивлению и определяется структурными

особенностями материала. С ростом температуры интенсифицируются колебания кристаллической решетки, а следовательно, увеличивается электрическое сопротивление.

Из опытных данных следует, что в расчетах, не требующих точности, можно допустить линейную зависимость удельного сопротивления и электрического сопротивления проводника от температуры в виде:

ρ = ρ0 (1 + α t ) = αρ0 Т , O м · м, R = R 0 (1 + α t ) = α R 0 Т , O м.

Здесь: ρ и ρ0 , R и R 0 — соответственно удельные сопротивления и электрические сопротивления проводника при t и 0 °С или Т и 273,15 K ; а = 273–1 K –1 — температурный коэффициент сопротивления для чистых металлов. Зависимость R = f ( T ) может быть представлена графиком (рис. 10.2). При некоторой достаточно низкой температуре Т k = 0,14 – 20 K , называемой критической, сопротивление скачком уменьшается до нуля. Это значит, что металл становится абсолютным проводником, то есть сверхпроводником. Впервые сверхпроводимость была обнаружена для ртути в 1911 г. голландским физиком Камерлинг-Онессом. Объясняется это явление с позиций квантовой теории. Использование сверхпроводящих материалов в обмотках электромагнитов, в блоках памяти компьютеров и т.п. практически исключается из-за их низких критических температур. В настоящее время, согласно научным публикациям в периодической печати, обнаружены и активно изучаются керамические материалы со сверхпроводимостью при температуре выше 100 K . Эффект температурной зависимости электрического сопротивления металлов используется в термометрах сопротивления, полупроводников — в термисторах. Точность измерения температуры термометрами сопротивления достигает 3·10 – 3 K , термисторами — 10 – 6 K .

Рис. 10.2

Величину, обратную электрическому сопротивлению, называют электрической проводимостью G = 1/ R , Ом–1 = См — сименс — проводимость участка электрической цепи сопротивлением 1 Ом.

Закон Ома может быть преобразован к иному виду, если в формулу (10.1) вместо R подставить значение сопротивления, следующее из (10.2):

I = U / (ρl / s ), A

и затем

Поскольку I / s = j , А/м2 — плотность тока; 1/ρ = γ — удельная электрическая проводимость вещества проводника, См/м, характеризующая его способность проводить электричество; U / l = Е — напряженность электрического поля в проводнике, В/м, то получим закон Ома, называемый условно законом Ома в дифференциальной форме

положительные заряды в каждой точке поля движутся в направлении вектора . Для изменения сопротивления участка цепи проводники соединяют последовательно, параллельно и смешанно. При последовательном соединении проводников (рис. 10.3) справедливы следующие соотношения между основными электрофизическими величинами:

I = const ;

θ 1 – θ 4 = U 1 + U 2 + U 3 ;

R = R 1 + R 2 + R 3 .

Рис. 10.3

Рис. 10.4

При параллельном соединении проводников (рис. 10.4) соотношения между этими же величинами имеют вид: θ1 – θ2 = U = const ;

I = I 1 + I 2 + I 3 ;

Разность потенциалов, электродвижущая сила и напряжение.

Работа и мощность тока. Закон Джоуля-Ленца. Закон Ома для полной цепи

известно, что при действии только сил электростатического поля на заряды происходит их перемещение в направлении меньшего потенциала. А работу,

совершаемую кулоновскими силами при перемещении единичного положительного заряда q = 1 Кл на участке 12 электрической цепи, называют разностью потенциалов θ1 — θ2 в точках 1 и 2 проводника

Перемещение носителей тока в этом случае приведет к выравниванию потенциалов во всех точках проводника и к исчезновению электрического поля. Поэтому для наличия постоянного тока в цепи необходимо иметь так называемый источник тока, способный создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения (рис. 10.5). Эти силы называют сторонними, так как действуют они на заряды со стороны источника тока. Природа сторонних сил может быть разной. В генераторах они возникают за счет механической энергии вращения ротора генератора в магнитном поле, в гальванических элементах — за счет энергии от химического реагирования между электродами и электролитом и т.п. Очевидна аналогия между источником тока в электрической цепи и, например, насосом в гидравлической системе. Действие сторонних сил обеспечивает движение зарядов против сил электростатического поля внутри источника тока. Благодаря этому на концах участка 12 поддерживается неизменной разность потенциалов, и в цепи течет постоянный электрический ток. Сторонние силы при этом совершают работу по перемещению носителей тока. Эту работу по перемещению единичного положительного заряда называют электродвижущей силой ЭДС источника тока, действующей в цепи или на участке 12 цепи

Рис. 10.5

Поскольку упомянутая работа энергетически обеспечивается источников тока, то величину е лучше называть электродвижущей силой источника тока в цепи. Таким образом, термин «электродвижущая сила» является характеристикой источника тока.

ЭДС, как и сила тока, — величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если ЭДС способствует движению положительных зарядов в выбранном направлении 1–2, то ε12 > 0. Если же ЭДС препятствует движению положительных зарядов в данном направлении, то ε12 < 0.

Электрическую цепь, в которой нет источника сторонних сил, принято рассматривать как однородный участок цепи (рис. 10.6). Основным свойством ее является отсутствие ЭДС. Есть также понятие неоднородного участка 12 цепи (рис. 10.7), который

следует характеризовать ЭДС ε12 и разностью потенциалов на его концах θ1 – θ2 . Подобная необходимость возникает от одновременного действия электростатических и сторонних сил F кул + F ст = ( E кул + E ст ) q , Н . При прохождении электрического тока по неоднородному участку 12 проводника над носителями тока совершается работа А 12 сторонних и электростатических сил:

A 12 = q ε12 + q (θ1 – θ2 ), Дж. (10.4)

Рис. 10.6

Рис. 10.7

Работу по перемещению единичного положительного заряда на участке 12 под действием указанных сил называют напряжением U 12 на данном участке цепи

Если на участке 12 сторонние силы отсутствуют, то напряжение на его концах равно разности потенциалов.

На основании изложенного, совершаемая в проводнике работа при перемещении заряда равна А = qU . Поскольку q = It , то за время t работа тока

А = IUt = I ( IR ) t = I 2 Rt = ( U 2 / R ) t , Дж,

а мощность тока

P = A / t = IU = I 2 R = U 2 / R , Вт.