Предел функции на бесконечности

Пусть независимая переменная хнеограниченно возрастает, т.е.хи функция определена на бесконечности.

 Число b называется пределом функции на бесконечности, если для любого, сколь угодно малого числа  >0 найдется такое число М() >0, что для всех х > М() выполняется неравенство .

Аналогично определяется предел функции при х - .

Дадим геометрическую интерпретацию предела функции на бесконечности. Как следует из определения предела, выбор -окрестности для точкиbна осиOY определяет числоМ>0, зависящее от выбранного, такое, что для всехх>Mзначенияy(x)попадают в-окрестность точкиb. Геометрически это означает, что график функцииy=y(x)неограничено приближается к прямойу=b, причем прих>Mграфик не выходит из "коридора" ограниченного прямымиу=b-иу=b+.

Если у функции существует конечный предел bприх, то у нее существует и горизонтальная асимптота (см. тему 5)у=b.

Хорошим примером функции, имеющей конечные пределы на +и -, причем эти пределы различны, является элементарная функцияy=arctgx(см. график в приложении)

Бесконечно малые (бм) величины. Сравнение бм величин

 Среди функций, изучаемых в математическом анализе, особо выделяют функции, имеющие предел, равный нулю – их называют бесконечно малыми; и функции, имеющие бесконечный предел – их называют бесконечно большими.

Обозначения:

ББ величины взаимосвязаны с БМ.

1. Во-первых, одна и та же функция может быть как БМ, так и ББ при различных условиях. Напримеру=х².

2. Во-вторых, если функцияу(х) является БМ в окрестности точких=аи не обращается в ноль в этой окрестности, то функция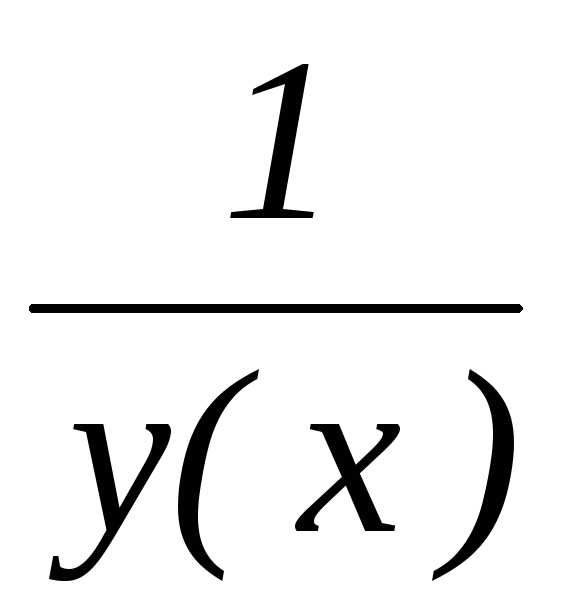является ББ в окрестности точких=а.

Если , то. Обратное также верно. Поэтому можно рассмотреть свойства и теоремы о БМ величинах, а затем, с соответствующими изменениями применить их к ББ величинам.

БМ величины часто обозначают буквами греческого алфавита: ,,и т.п. Пусть. Причем в условии вычисления пределов в качестве предельного значения переменнойхможет выступать не только конечное числоа, но и.

При дальнейшем вычислении пределов функций мы будем пользоваться следующими свойствами БМ величин:

1.  Сумма конечного числа БМ есть величина БМ :

2.  Произведение конечного числа БМ есть величина БМ :.

3.  Произведение ограниченной или постоянной величины и БМ есть величина БМ :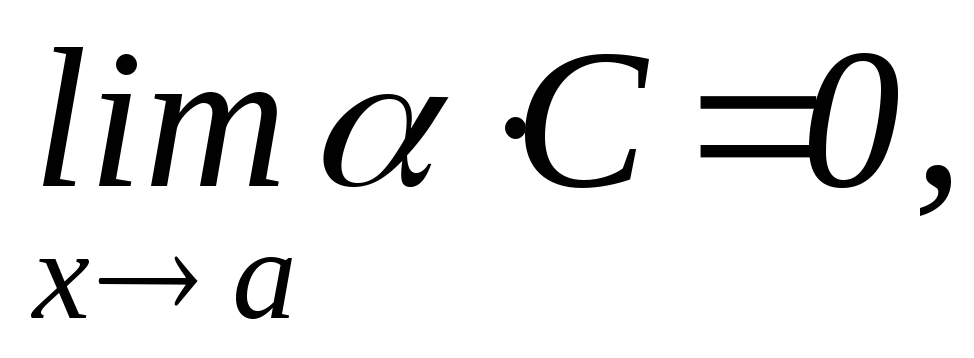гдеС-constили.

 Сравнить две БМ– это значит вычислить предел их отношения и по полученному результату сделать вывод о том, какая из величин быстрее стремится к нулю или они одинаково быстро стремятся к нулю и т.п. Все возможные варианты можно подразделить следующим образом.

1. Если , тобыстрее стремится к нулю, чеми называется БМ более высокого порядка, чем.

2. Если , тобыстрее стремится к нулю, чеми называется БМ более высокого порядка, чем. Здесь ситуация обратная случаю 1, если поменять местамии: .

3. Если 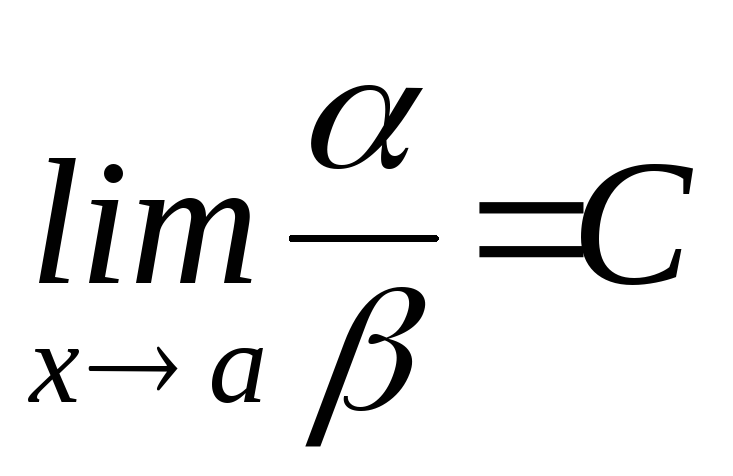(С=const0), значит и- БМ одного порядка малости.

Если т.е.БМ называютсяэквивалентными. Это важнейший частный случай БМ величин одного порядка

 Если , то-эквивалентны(справедливо и для ББ величин).

Вычисление пределов существенно упрощается, если применить теоремы об эквивалентных БМ величинах.

 Теорема 1.Еслииприха, то. Т.е. можно заменять БМ величины эквивалентными при вычислении пределов отношений (эта теорема справедлива также для эквивалентных ББ величин).

 Теорема 2.В сумме, состоящей из БМ величин разного порядка, можно отбросить БМ величины болеевысокогопорядка и оставшаяся часть будет эквивалентна всей сумме.

Для ББ величин эта теорема также справедлива, с соответствующей поправкой: в конечной сумме ББ величин можно отбросить ББ более низкогопорядка.

Например, у(х)=х³+2х²-х. Эта функция будет БМ прих0, тогдау(х)=3х³+2х²-х -х(отброшены БМ величины более высоких порядков). Та же функция будет ББ прих, тогдау(х)=3х³+2х²-х 3х³(отброшены ББ величины более низких порядков).

 Оставшаяся после отбрасывания, эквивалентная исходной, часть БМ (или ББ) величины называется ее главной частью. Один из технических приемов вычисления пределов –выделение главной части.