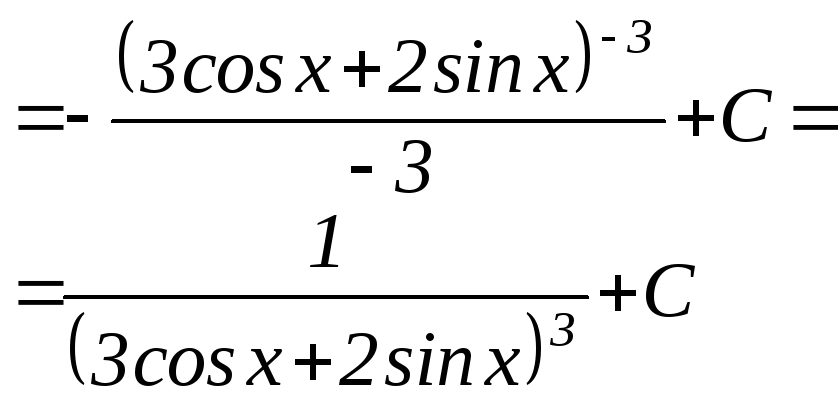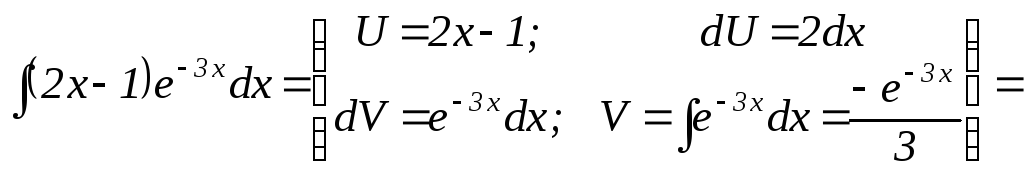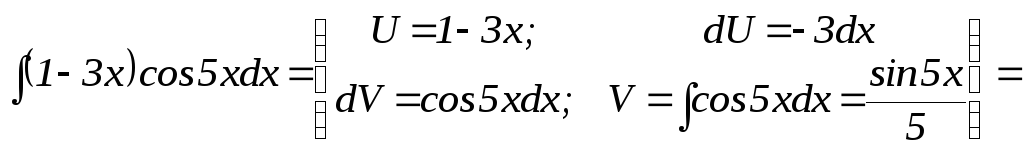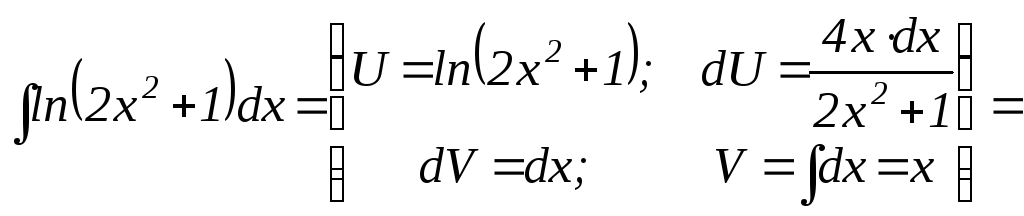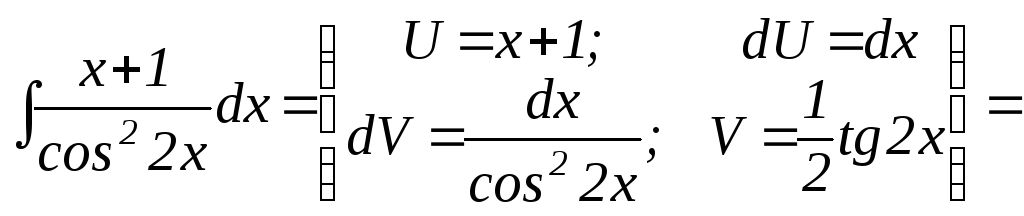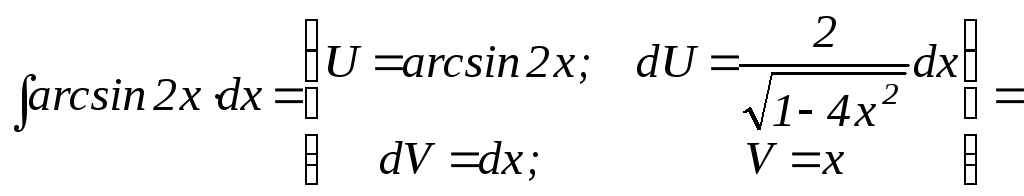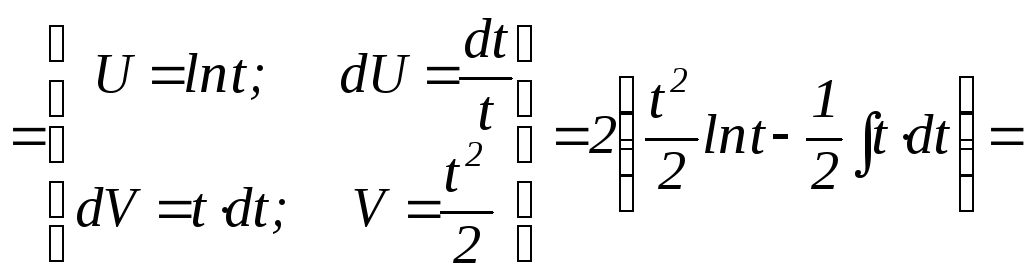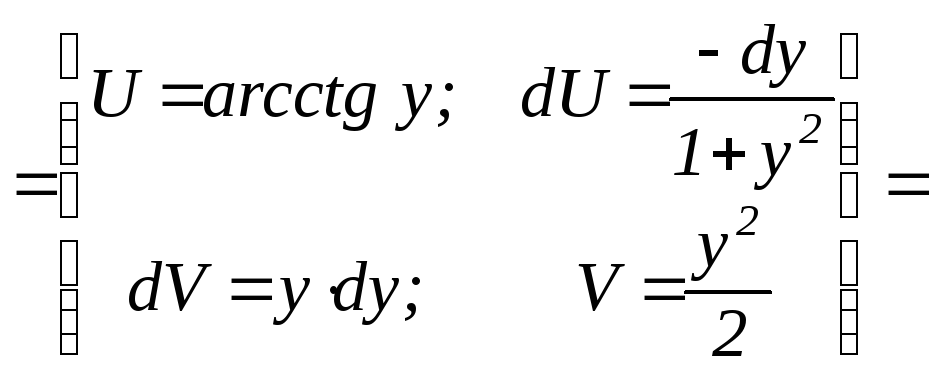Тема 7. Примеры Примеры выполнения обязательных заданий по теме 6
Задание 1. Найти неопределенные интегралы.
,
Вычисление неопределенных интегралов №№ 1, 2 основано на методе "внесение под знак дифференциала" (см. теорию по теме 6, Методы интегрирования). В теоретической части приведена таблица основных вариантов таких внесений. В объяснениях к примерам приводятся формулы для конкретных случаев.
, Примеры
|
|
Для
приведения к табличным интегралам
выполняется тождественное преобразование:
|
|
|
Разбиваем
на сумму двух интегралов и вносим под
знак дифференциала
|
|
= = |
Получаем
табличные степенные интегралы вида
|
в числителе функции.
=
.
,
и
.
|
|
Разбиваем интеграл на сумму двух интегралов. | ||
|
= |
Вносим
под знак дифференциала
| ||
|
= |
и
| ||
в первом интеграле
во втором. Получаем табличные интегралы:
логарифмический и степенной, при
.
|
|
Здесь
вносим под знак дифференциала
|
.
|
|
К
интегралу вида арксинус приводим,
внося под знак дифференциала
|
.
|
|
Вносим
под знак дифференциала
|
|
|
сумму двух интегралов. |
.
Разбиваем на
|
|
Разбиваем
на сумму двух интегралов. Вносим под
знак дифференциала
|
|
|
Первый
интеграл – степенной,
|
.
,
второй тригонометрический, вида
котангенс.
|
|
Разбиваем на сумму двух интегралов. | ||
|
|
Вносим под знак дифференциала в первом интеграле | ||
|
|
| ||
=
,
во втором:
.
Оба полученных интеграла являются
степенными.
|
|
В числителе стоит производная знаменателя с обратным знаком: | |
|
|
| |
.
После внесения под знак дифференциала
получаем степенной интеграл,
.
|
|
Учтем, что
|
|
дифференциала. Получили логарифмический интеграл. | |
и
внесем производную под знак
- При выполнении данного задания следует повторить правила вычисления производных, особенно – производных сложных функций.
,
Неопределенные интегралы №№ 3,4 вычисляются методом интегрирования по частям, № 4 – вместе с заменой переменной.
- 
- формула интегрирования по частям.
, ПРИМЕРЫ
|
|
В соответствии с рекомендациями, приведенными в теории, | |
|
|
разбиваем
интеграл на части
| |
|
|
делаем алгебраические преобразования и получаем ответ. | |
|
-
Обратите
внимание на вычисление интеграла
("внесение под знак дифференциала"):
| ||
и
,
,
произвольная постоянная прибавляется
только один раз.
|
|
| ||||
|
|
Аналогично предыдущему интегралу. |
| |||
|
- Обратите внимание на вычисление интеграла ("внесение под знак дифференциала"):
|
| ||||
|
|
|
Разбиваем на части в соответствии с рекомендациями. | |||
|
|
|
Для
вычисления интеграла
| |||
|
|
|
Разбиваем на два интеграла. | |||
,
или
,
произвольная постоянная прибавляется
только один раз.
в числителе.
|
|
Разбиваем на части в соответствии с рекомендациями. |
|
|
Полученный интеграл – из неосновной таблицы. |
|
- Обратите внимание на вычисление интеграла ("внесение под знак дифференциала"):
| |
,
и
.
|
|
Разбиваем на части в соответствии с рекомендациями. | |
|
|
| |
|
|
| |
и
.
|
|
Разложим синус двойного угла и внесем под знак дифференциала. |
|
|
Заменим переменную. |
|
|
Интегрируем по частям, переходим к старой переменной. |
|
|
|
|
|
Внесем под знак дифференциала. | |
|
|
Заменим переменную. | |
|
|
Интегрируем по частям. Табличный интеграл:
| |
|
| ||
|
|
В данном случае лучше выбрать второй вариант. Переходим к старой переменной. | |
.
|
|
Заменим переменную. |
|
|
Интегрируем по частям. |
|
|
Переходим к старой переменной. |
- Аналогично примерам 6-8 вычисляются, например, такие интегралы:
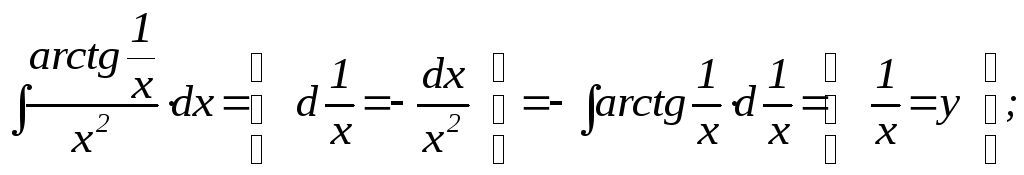и
далее – по частям.
При вычислении интеграла № 5 используется прием: выделение полного квадрата. С помощью такого приема можно вычислять интегралы вида:
|
|
|
|
|
|
с
квадратным трехчленом в некоторой
степени в знаменателе, где
- выделенный полный квадрат (
).