
- •Тема 5. Теория
- •Тема 5. Дифференциальное исчисление функции одного аргумента Приращения функции и аргумента
- •Дифференцирование функции одной переменной (производная и дифференциал) Производная функции
- •Основные правила дифференцирования
- •Производная сложной функции
- •Примеры
- •Производная неявно заданной функции
- •Производная параметрически заданной функции
- •Логарифмическое дифференцирование (логарифмическая производная)
- •Дифференциал функции и дифференциал аргумента
- •Производные и дифференциалы высших порядков
- •Вычисление пределов по правилу Лопиталя
- •Пример – иллюстрирует случай неприменимости правила Лопиталя.
- •Примеры
Тема 5. Теория
Сложные проценты. Воспользуемся формулой An=A(1+r)n , A4=10(1+0,8)4=104,98 млн. денежных единиц.
Вывод. При одной и той же процентной ставке и первоначальной сумме вклада рост при вкладе под сложные проценты происходит значительно быстрее, чем при вкладе под простые проценты.
2)
Найдем
наращенное значение вклада по кварталам
4-го года, воспользовавшись формулой
для равномерного начисления процентов:
![]() гдеm=4
(начисление
поквартально), n=4
, r=0,8,
A=10.
Тогда
гдеm=4
(начисление
поквартально), n=4
, r=0,8,
A=10.
Тогда
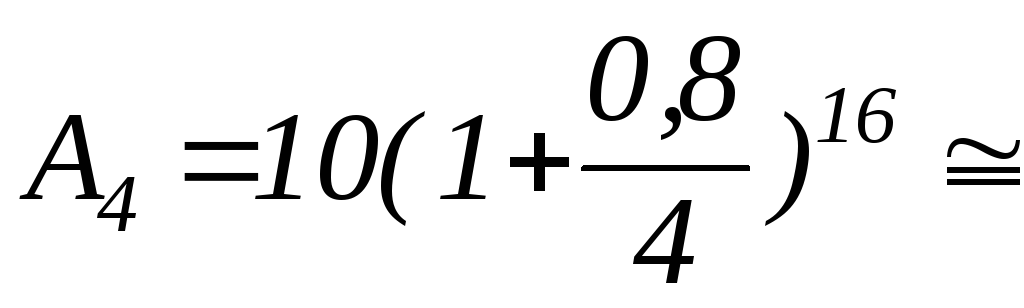 184,88
млн.ден.ед.
184,88
млн.ден.ед.
Найдем
наращенное значение вклада в конце 4-го
года при ежемесячном начислении
процентов. В той же формуле теперь m=12,
остальные значения – те же
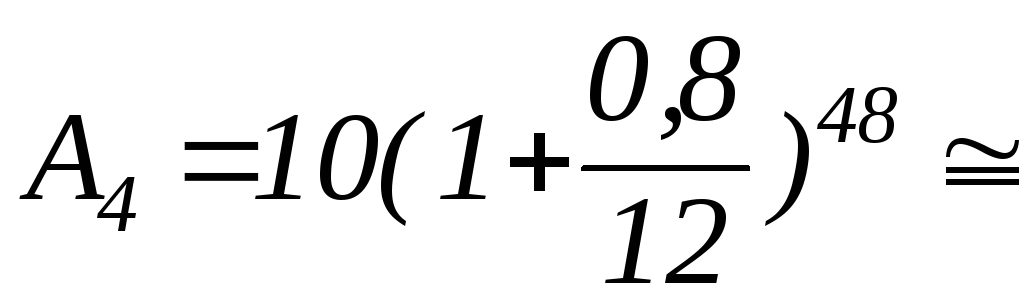 221,50
млн.ден.ед.
221,50
млн.ден.ед.
Вычислим еще наращенное значение вклада по формуле непрерывного начисления процентов:
An=Aer n; A4=10e0,84=10e3,2=245,33 млн.ден.ед.
Вывод. Рост денежного вклада существенно зависит от числа m , т.е. от того, сколько раз в год начисляются сложные проценты. Чем больше m, тем быстрее растет вклад.
3) Увеличение первоначального вклада в 1,5 раза : An=1,5·A=15 млн.ден.ед. Рассчитаем требуемые величины :
|
по основной формуле начисления сложных процентов |
по формуле непрерывного начисления процентов |
|
|
|
|
|
|
|
|
|
Сравнение результатов показывает, что существенная разница наблюдается только при вычислении дисконтируемой суммы.
Тема 5. Дифференциальное исчисление функции одного аргумента Приращения функции и аргумента
Пусть х – аргумент (независимая переменная); y=y(x) – функция.
В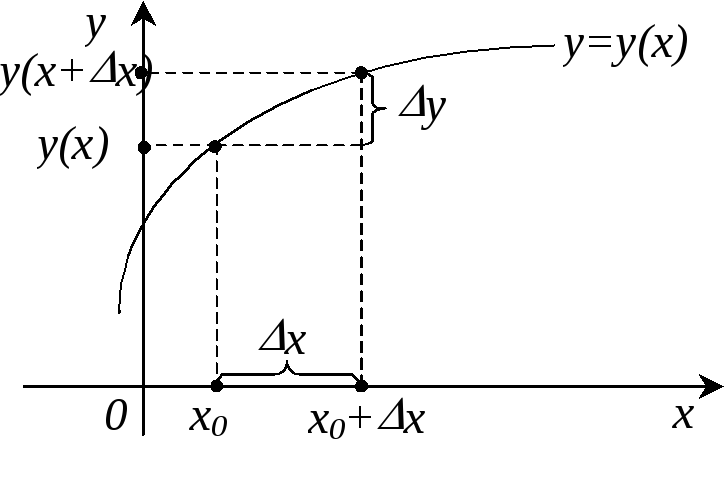 озьмем
фиксированное значение аргументах=х0
и вычислим значение функции y0=y(x0).
Теперь произвольным образом зададим
приращение
(изменение)
аргумента и обозначим его
х
(
х
может быть любого знака).
озьмем
фиксированное значение аргументах=х0
и вычислим значение функции y0=y(x0).
Теперь произвольным образом зададим
приращение
(изменение)
аргумента и обозначим его
х
(
х
может быть любого знака).
Аргумент с приращением – это точка х0+ х. Допустим, в ней также существует значение функции y=y(x0+ х) (см. рисунок).
Таким образом, при произвольном изменении значения аргумента получено изменение функции, которое называется приращениемзначения функции :
![]() ,
,
и
не является произвольным, а зависит от
вида функции и величины
![]() .
.
Приращения аргумента и функции могут быть конечными, т.е. выражаться постоянными числами, в этом случае их иногда называют конечными разностями.
В экономике конечные приращения рассматриваются весьма часто. Например, в таблице приведены данные о длине железнодорожной сети некоторого государства. Очевидно, приращение длины сети вычисляется путем вычитания предыдущего значения из последующего.
Будем рассматривать длину ж/д сети как функцию, аргументом которой будет время (годы).
|
Годы |
Длина ж/д на 31.12, тыс.км. |
Приращение |
Среднегодовой прирост |
|
1993 |
74,5 |
76,9-74,5=2,4 |
2,4/3=0,8 |
|
1996 |
76,9 |
81,0-76,9=4,1 |
4,1/4=1,0 |
|
2000 |
81,0 |
83,5-81,0=2,5 |
2,5/3=0,8 |
|
2003 |
83,5 |
84,4-83,5=0,9 |
0,9/1=0,9 |
|
2004 |
84,4 |
|
|
Само по себе приращение функции (в данном случае длины ж/д) сети) плохо характеризует изменение функции. В нашем примере из того, что 2,5>0,9 нельзя заключить, что сеть росла быстрее в 2000-2003 годах, чем в 2004 г., потому что приращение 2,5 относится к трехлетнему периоду, а 0,9 – всего к одному году. Поэтому вполне естественно, что приращение функции приводят к единице изменения аргумента. Приращение аргумента здесь – периоды: 1996-1993=3; 2000-1996=4; 2003-2000=3; 2004-2003=1.
Получим то, что в экономической литературе называют среднегодовым приростом.
Можно избежать операции приведения приращения к единице изменения аргумента, если взять значения функции для значений аргумента, отличающихся на единицу, что не всегда возможно.
В математическом анализе, в частности, в дифференциальном исчислении, рассматривают бесконечно малые (БМ) приращения аргумента и функции.

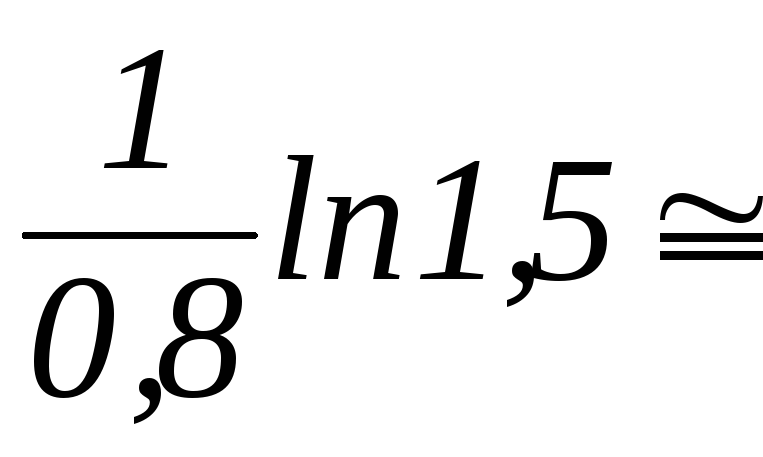 0,51
0,51 =
=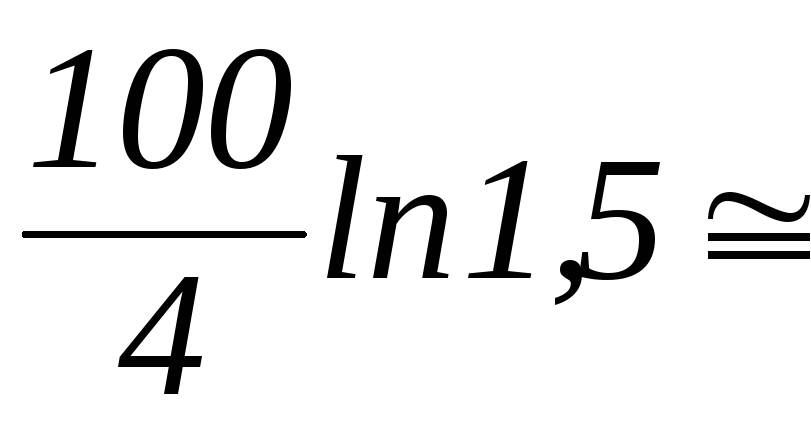 10,14
10,14