•которое легче интегрируется, если перейти к полярной системе координат (r, φ). После подстановки получим , откуда:

•Рассмотрим характер движения изображающей точки по фазовым траекториям. Умножая первое из уравнений (4.17) на u, а второе на v и складывая, получаем:

где

•Пусть a1 < 0 (a1=Reλ). Изображающая точка тогда непрерывно приближается к

началу координат, не достигая его в конечное время. Это означает, что фазовые траектории представляют собой скручивающиеся спирали и соответствуют затухающим колебаниям переменных. Это – устойчивый фокус.

•В случае устойчивого фокуса, как и в случае устойчивого узла, выполнено не только условие Ляпунова, но и более жесткое требование. Именно, при любых начальных отклонениях система по прошествии времени вернется как угодно близко к положению равновесия. Такая устойчивость, при которой начальные отклонения не только не нарастают, но затухают, стремясь к нулю, называют

абсолютной устойчивостью.

•Если в формуле (4.18) a1 >0, то изображающая точка удаляется от начала

координат, и мы имеем дело с неустойчивым фокусом. При переходе от плоскости u,v к фазовой плоскости x,y спирали также останутся спиралями, однако будут деформированы.

•Рассмотрим теперь случай, когда a1=0. Фазовыми траекториями на плоскости u, v

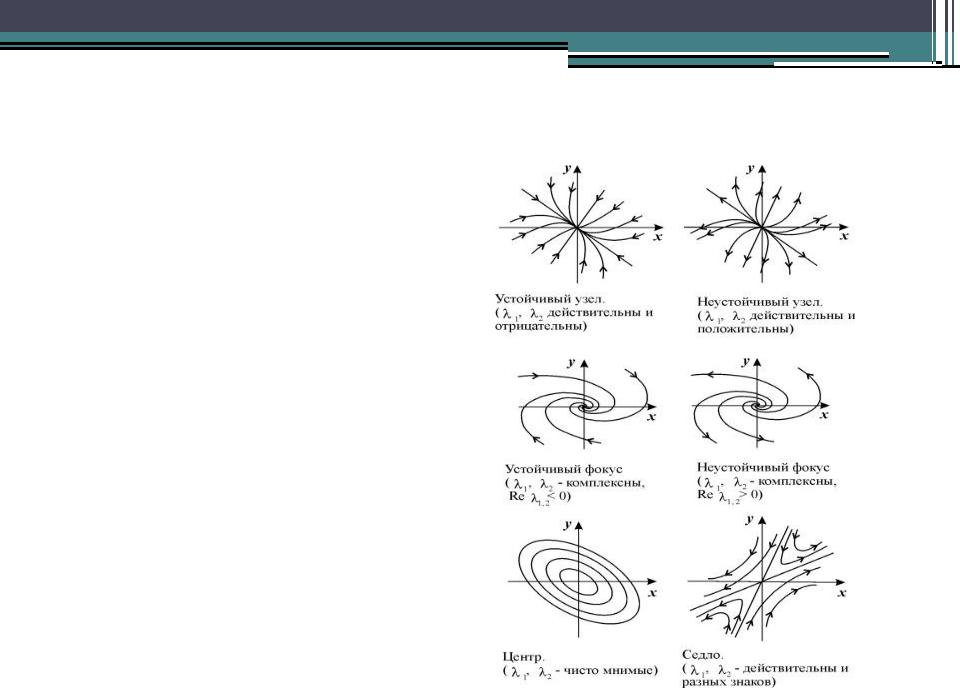
•Таким образом, при a1=0 через

особую точку x=0, y=0 не проходит ни одна интегральная кривая. Такая изолированная особая точка, вблизи которой интегральные кривые представляют собой замкнутые кривые, в частности, эллипсы, вложенные друг в друга и охватывающие особую точку, называется центром.

•Таким образом, возможны шесть типов состояния равновесия в зависимости от характера корней характеристического уравнения (4.7). Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 4.9.

• Введем обозначения:

Бифуркационная диаграмма

(4.11)

• Тогда характеристическое уравнение запишется в виде:

(4.12)

•Рассмотрим плоскость с прямоугольными декартовыми координатами ,и отметим на ней области, соответствующие тому или иному типу состояния равновесия, который определяется характером корней характеристического уравнения

(4.13)

•Условием устойчивости состояния равновесия будет наличие отрицательной действительной части у 1 и 2. Необходимое и достаточное условие этого – выполнение неравенств > 0, > 0.

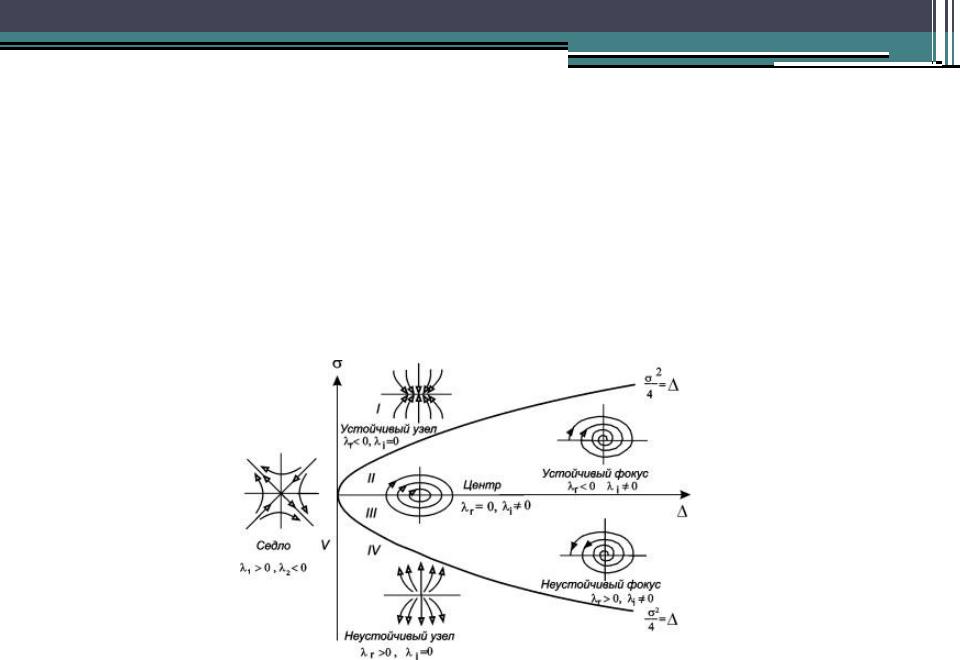
•На диаграмме (4.15) этому условию соответствуют точки, расположенные в первой четверти плоскости параметров. Особая точка будет фокусом, если 1 и 2 комплексны. Этому условию соответствуют те точки плоскости, для которых , т.е. точки между двумя ветвями параболы 2 = 4 . Точки полуоси = 0, >0, соответствуют состояниям равновесия

типа центр. Аналогично, 1 и 2 - действительны, но разных знаков, т.е. особая точка будет седлом, если <0, и т.д. В итоге мы получим диаграмму разбиения плоскости параметров , , на области, соответствующие различным типам состояния равновесия.

•Если коэффициенты линейной системы a, b, c, d зависят от некоторого параметра, то при изменении этого параметра будут меняться и величины, . При переходе через границы характер фазового портрета качественно меняется. Поэтому такие границы называются бифуркационными – по разные стороны от границы система имеет два топологически различных фазовых портрета и, соответственно два разных типа поведения.

•На диаграмме видно, как могут проходить такие изменения. Если исключить особые случаи – начало координат, – то легко видеть, что седло может переходить в узел, устойчивый или неустойчивый при пересечении оси ординат. Устойчивый узел может перейти либо в седло, либо в устойчивый фокус, и т.д. Отметим, что переходы устойчивый узел – устойчивый фокус и неустойчивый узел – неустойчивый фокус не являются бифуркационными, так как топология фазового пространства при этом не меняется. Более подробно мы поговорим о топологии фазового пространства и бифуркационных переходах в лекции 6.

•При бифуркационных переходах меняется характер устойчивости особой точки. Например, устойчивый фокус через центр может переходить в неустойчивый фокус. Эта бифуркация называется бифуркацией Андронова- Хопфа по именам исследовавших ее ученых. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной (см. лекцию 8).

ЛЕКЦИЯ 5 ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙ НЕЛИНЕЙНЫХ СИСТЕМ ВТОРОГО ПОРЯДКА

•Математический анализ поведения траекторий этой системы на фазовой плоскости связан с именами французского математика Анри Пуанкаре и русского математика и механика Александра Михайловича Ляпунова (1857-1918).

•Ляпунов показал, что в большом числе случаев анализ устойчивости стационарного состояния нелинейной системы можно заменить анализом устойчивости системы, линеаризованной в окрестности стационарного состояния.

•Рассмотрим характер поведения переменных при некотором небольшом отклонении системы от состояния равновесия. Введем вместо переменных x, y новые независимые переменные, , определив их как смещения относительно равновесных значений переменных

(5.4)

•Подставив эти выражения в (5.1), получим:

(5.5)