ЛЕКЦИЯ 17
Оценка регрессионных характеристик
Пусть проводится n независимых опытов, в каждом из которых двухмерная случайная величина (Х,У) принимает определенные значения и результаты опытов представляют собой двумерную выборку вида {(х1, у1), (х2, у2),…,(хn, уn)}. Необходимо на основании имеющейся выборки выявить характер связи между величинами X, Y, т.е. получить оценку условного
математического ожидания mY* / x − оценку регрессии Y на х. Данная оценка представляет собой некоторую функцию:
mY* / x = y ( x) = ϕ( x, a0 , a1 ,..., am ) ,
где a0,a1,...,am – неизвестные параметры.
Таким |
образом, |
во-первых, |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
необходимо |
установить |
тип |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
зависимости ϕ(x,a0,a1,...,am) – т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
является |
ли |
она |
линейной, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратичной, показательной и т.д., |
|
|
|
|
|
|
|
|
|
|
|
|
|
· |
||||
во-вторых, |
определить |
значения |
|
|
|
|
|
|
|
|
|
|
|
|
· |
|||
неизвестных параметров a0,a1,...,am . |
|
|
|
|
|
|
|
|
|
|
|
|
· |
|||||
· · |
|
|
|
|
|
|
|
|
|
· |
· |
· |
|
|||||
Для определения типа зависимости |
· |
|
|
|
|
|
|
· |
|
|
||||||||
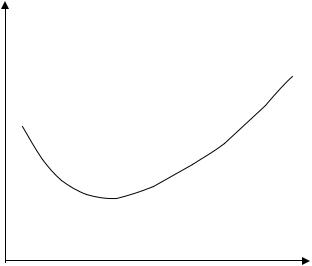
строится диаграмма рассеивания |
· |
|
· |
· |
· · |
|
· |
· |
· |
|
|
|||||||
или корреляционное поле, которую |
· |
· |
· |
· |
· |
· |
· |
|
|
|
||||||||
можно получить, если результаты |
|
|
|
· |
· |
|
|
|
|
|
|
|
||||||
опытов изобразить в виде точек на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
плоскости |
в |
декартовой системе |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
координат |
(см. рисунок). |
На |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
основании анализа корреляционного поля выбираем тип эмпирической линии регрессии y ( x) = ϕ( x, a0 , a1 ,..., am ) , которая должна проходить через точки
(х1,y1)....(xn,yn) так, чтобы ее график наилучшим образом соответствовал бы к неизвестной линии регрессии, т.е. ее значения должны быть приблизительно равны средним арифметическим значений Y для каждого значения Х=х. Во многих случаях тип зависимости может быть выбран на основе теоретических или иных соображений.
Для определения значений параметров, при которых обеспечивается наилучшее согласования кривой y = ϕ( x, a0 , a1 ,..., am ) и экспериментальных точек {(х1, у1), (х2, у2 ,…, (хn, уn)}, используется метод наименьших квадратов.
|
Метод наименьших квадратов |
Суть |
данного метода заключается в том, что значения параметров |
a0,a1,...,am |
необходимо выбрать так, чтобы сумма квадратов отклонений |
экспериментальных точек от сглаживающей кривой обращалась в минимум:
∑n [yi − ϕ ( xi , a 0 , ..., a m ) ]2 = m in |
(17.1) |
i =1 |
|
Найдем значения aj , j =1,..., m , обращающие левую часть выражения (17.1) в
минимум. |
Для этого продифференцируем его по aj , j =1,..., m , |
и приравняем |
|||
производные к нулю (в точке экстремума производная равна нулю): |
|||||
|
|
n |
∂ϕ( xi ) = 0, j = 0,1,...m , |
|
|
|
|
∑[yi −ϕ( xi , a0 ,..., am )] |
(17.2) |
||
|
|
i =1 |
∂a j |
|
|
где |
∂ϕ(xi ) |
– значение частной производной функции ϕ по параметру a j в |
|||
∂a j |
|||||
|
|
|
|
||
точке хi.
Система уравнений (17.2) содержит столько же уравнений, сколько неизвестных параметров, т.е. m+1.
Решить систему (17.2) в общем виде нельзя; для этого необходимо задаться конкретным видом функции ϕ.
Пусть y представляет собой степенной ряд:
|
|
|
|
|
m |
|
|
|
|
|
y = ϕ( x, a0 ,..., am ) = ∑ a j x j . |
(17.3) |
|
|
|
|
|
|
j =0 |
|
Тогда (17.2) примет вид системы линейных уравнений (СЛУ): |
|
|||||
|
|
|
m |
n |
n |
|
|
|
|
∑a j ∑(xi )j +k |
= ∑ yi (xi )k , k = 0,1,...., m |
(17.4) |
|
|
|
|
j=0 i=1 |
i=1 |
|
|
Поделим обе части уравнений на объем выборки n, система примет вид |
|
|||||
|
|
|
|
m |
|
|
|
|
|
|
∑ajαˆ j+k (xi ) =αˆk,1(xi , yi ), k = 0,1,...., m |
(17.5) |
|
|
|
|
|
j=0 |
|
|
где αˆk ( x) = |
1 |
n |
|
|
|
|
∑(xi )k - оценка начального момента k-го порядка величины X; |
||||||
|
n |
i=1 |
n |
|
|
|
αˆk ,1 ( x , |
y ) = 1 |
|
|
|
||
∑ xik yi – оценка смешанного начального момента порядка |
||||||
|
|
n |
i=1 |
|
|
|
k+1 величин X и Y.
Переменными в системе (17.4) являются aj , j =1,..., m , а вычисленные по исходной выборке оценки начальных моментов являются коэффициентами
СЛУ. Решив данную систему, |
мы определим оценки параметров aˆ0,aˆ1,...,aˆm , |
обеспечивающие наилучшее |
согласование кривой y = ϕ( x, a0 , a1 ,..., am ) и |
экспериментальных точек {(х1, у1), (х2, у2),…,(хn, уn)}. |
|
Пример. Определим оценку линейной регрессии mY / x = a0 + a1x. |
|
Система (17.5) для m=1 имеет вид |
|
αˆ |
0 |
(x)a0 |
+αˆ |
(x)a1 |
=αˆ |
0,1 |
(x , y ) |
|
1 |
|
|||||
|
|
(x)a0 |
+αˆ2 (x)a1 |
=αˆ1,1(x , y ) . |
|||
αˆ1 |
|||||||
|
|
|
|
|
|
|
|
С учетом того, что αˆ 0 ( x ) = 1, αˆ1 ( x ) = x , αˆ 0 ,1 ( x , y ) = y , получаем:
|
a |
+ xa = y |
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
αˆ2 (x)a1 =αˆ1,1(x , y ) . |
|
|||
|
xa0 + |
|
|||||
|
|
|
|
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
aˆ1 = |
αˆ1 ,1 ( x |
, y ) − x y |
= |
K *X Y |
, |
(17.6) |
|
|
αˆ 2 ( x ) − x 2 |
|
|||||
|
|
|
S 02 ( x ) |
|
|||
|
|
|
aˆ0 = y −aˆ1 x , |
|
|
|
(17.7) |
что соответствует уравнениям прямых регрессий (9.10) (см. лекцию 9).