ЛЕКЦИЯ 7
Функции одного случайного аргумента
Пусть некоторая случайная величина Х подвергается детерминированному преобразованию ϕ, в результате которого получится величина Y, т.е. Y =ϕ(x).
Очевидно, что величина Y будет случайной, и, как правило, необходимо определить закон распределения и/или числовые характеристики случайной величины Y по известному закону распределения величины Х и виду преобразования ϕ.
Закон распределения функции случайного аргумента
В случае, если Х – дискретная случайная величина с известным рядом распределения вероятностей, определение ряда вероятностей Y не составит
сложности.
xi |
x1 |
x2 |
… |
xn |
pi |
p1 |
p2 |
… |
pi |
|
|
|
… |
|
yi |
ϕ(x1) |
ϕ(x2) |
ϕ(xn) |
|
pi |
p1 |
p2 |
… |
pn |
(*) |
|
|
… |
|
|
|
|
|
|
yi |
y1 |
y2 |
ym |
|
pj |
p1 |
p2 |
… |
pm |
(**) |
|
|
|
|
Из (*) путем упорядочивания и объединения одинаковых значений получаем ряд распределения случайной величины Y (**).
Если Х – непрерывная случайная величина с известной плотностью
вероятности f (x) , то алгоритм получения закона распределения Y =ϕ(x) зависит от вида ϕ. Рассмотрим участок оси абсцисс [а, b], на котором лежат все возможные значения величины Х, т.е. p(a ≤X ≤b) =1, в частном случае a = −∞,b = +∞ . Способ решения поставленной задачи зависит от поведения
функции ϕ на участке [а, b]: монотонна она на этом участке или нет. При этом отдельно проанализируем два случая: монотонного возрастания и монотонного убывания функции.
Y = ϕ(х) – монотонно возрастающая функция. Определим функцию распределения G( y) случайной величины У. По определению она равна
ψ ( y )
G( y) = p(Y < y) = p(ϕ(x) < y) = p( X <ψ ( y)) = ∫ f X (x)dx ,
−∞
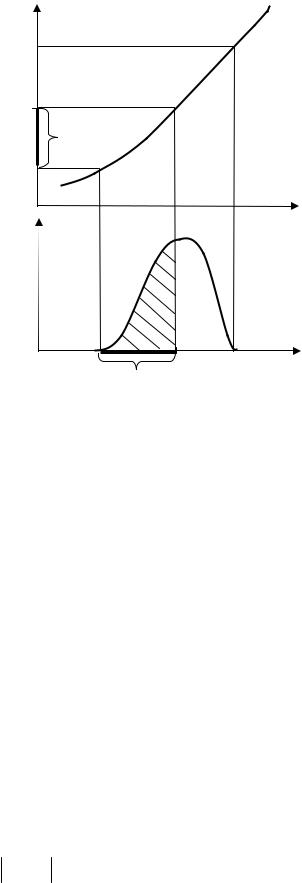
где ψ(y) – обратная функция ϕ(x). Для выполнения условия Y < y
необходимо и достаточно, чтобы случайная величина Х попала на участок оси абсцисс от а до ψ(y). Таким образом, функция распределения Y для аргумента X, распределенного в интервале [a, b], равна
0, y <ψ (a), |
|
ψ ( y ) |
|
|
∫ fX (x)dx,ψ (a) ≤ y ≤ψ (b), |
G( y) = |
|
|
a |
1, y >ψ (b).
Y = ϕ(х) – монотонно убывающая функция. Определим функцию распределения G( y) случайной величины Y. По определению она равна
G( y) = p(Y < y) = p(ϕ(x) < y) =
Y =ϕ(x)
ψ(b)
y
Y<y
ψ(a)
x
f (x)
x
a |
ψ(y) b |
|
X<ψ(y) |
p( X >ψ ( y)) = |
∞∫ f X (x)dx, |
|
ψ ( y ) |
где ψ(y) – обратная функция ϕ(x).
Для выполнения условия Y < y необходимо и достаточно, чтобы
случайная величина Х попала на участок оси абсцисс от х = ψ(y) до b. Таким образом, функция распределения Y для аргумента X, распределенного в интервале [a, b], равна:
0, y <ψ(b),
b
G(y) = ∫ fX (x)dx,ψ(b) ≤ y ≤ψ(a),
ψ ( y)
1, y >ψ(a).
Плотность вероятностей случайной величины Y =ϕ(x) монотонного случая имеет следующий вид:
0, y < ymin ,
g(y) = G′(y) = fX (ψ(y)) ψ′(y) , ymin ≤ y ≤ ymax ,
0, y > ymax .
для любого
(7.1)
Пример. Пусть случайная величина Х имеет нормальный закон распределения
f(x) = |
1 |
e |
−x 2 /2 σ 2 |
, |
Y = |
X |
3 |
2 π |
|
. Найти |
|||||
σ |
|
|
|
|
|
|
|
g( y ). |
|
|
|
|
|
|
|
Функция |
Y =ϕ(x) |
|
строго |
||||
монотонна, дифференцируема и имеет
обратную X = ψ(y) = 3 |
Y . Воспользуемся |
||||||||||||||||||
формулой(7.1). Таккак |
1 |
|
|
||||||||||||||||
|
fX (ψ ( y)) = fX ( y1/ 3 ) = |
|
|
|
|
e− y2 / 3 / 2σ 2 , |
|||||||||||||
σ |
2π |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
′ |
|
|
|
|
1/ 3 |
′ |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ψ ( y) |
|
= |
|
( y |
|
|
) |
= |
|
|
, |
|
|
|
|
|||
|
|
|
3y2 / 3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то искомая |
плотность |
распределения |
|||||||||||||||||
функции Y = X 3 : |
1 |
|
|
|
|
|
|
|
|||||||||||
|
g ( y) = |
|
|
|
|
|
|
|
|
e− y2 / 3 / 2σ 2 . |
|||||||||
|
3σ y |
2 / 3 |
2π |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Y = ϕ(х) – немонотонная функция. Алгоритм получения закона распределения Y =ϕ(x) приведен ниже.
Y =ϕ(x)
ψ(b)
y
Y<y
ψ(a)
x
f (x)
x
a ψ(y) |
b |
X>ψ(y)
1.Построить график Y = ϕ(х) и определить диапазон значений Y [ymin, ymax].
2.Диапазон Y разбить на M интервалов, в каждом из которых одинаковая степень неоднозначности ki, i = 1, 2, ..., M:
[ymin, y1), [y1, y2) … [yM-1, ymax].
Степень неоднозначности ki – число значений Х, соответствующих одному значению Y, или число обратных функций для данного интервала ψj(у), j = 1, …, ki.
3.Определить обратные функции ψj(у) = ϕ–1(х) и вычислить ψj'(у) .
Вобщем случае число обратных функций ψj(у) в i-м интервале равно ki.
4.Определить плотность вероятностей g(y) по следующей формуле:
0, y < ymin , |
|
|
||||||
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
ki |
|
|
ψ ′j ( y ) |
|
, yi −1 |
≤ y < yi , |
(7.2) |
|
|
|
||||||
g ( y ) = |
∑ f X (ψ j ( y )) |
|
||||||
j =1 |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
0, y > y |
|
. |
|
|
|
|
|
|
max |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
В частном случае, когда обратные функций одинаковы для всех интерваловψ′j ( y) =ψ′( y), ψ′j ( y) = ψ′( y) , формула (7.2) принимает вид
|
0, y > |
ymax . |
|
|
|
||
|
0, y < |
ymin , |
|
|
|
|
|
M |
|
|
|
|
|
(ψ ( y )) ψ ′( y ) , yi −1 ≤ y < yi , , |
(7.3) |
g ( y ) = ki f X |
|||
|
|
|
|
M |
|
|
|
а если величина Х равномерно распределена в интервале [a, b], т.е. ее плотность
равна |
1/(b−a), a ≤ x ≤b |
|
|
|
|
|
|
|
|||
fX (x) = |
0, x <a, x >b |
, то выражение для g(у) можно представить как |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 , y < |
y m in , |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
ψ ′( y ) |
|
|
|
|
|
g ( y ) = |
k i |
|
|
, y i −1 ≤ y |
< y i , |
(7.4) |
|||
|
|
b − a |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
0 , y > |
y m a x . |
|
|
||||
|
|
|
|
|
|
||||||
Числовые характеристики функции случайного аргумента
Пусть Y = ϕ(х), где X – случайная величина с известным законом распределения, и необходимо определить числовые характеристики Y. В том случае, когда закон распределения Y определен (см. выражения (7.1 − 7.4)), то числовые характеристики Y легко вычислить по формулам (5.1 − 5.7). Однако, если закон распределения величины Y в явном виде не нужен, а необходимы только ее числовые характеристики, применимы следующие формулы.
Если Х – дискретная случайная величина с известным рядом распределения вероятностей, то
m Y = |
M [Y ] |
= ∑n |
ϕ ( x i ) p i ; |
|
(7.5) |
||||
|
|
|
|
|
i = 1 |
|
|
|
|
D Y = M [Y 2 ] − m Y |
2 |
= |
∑n |
|
ϕ 2 ( x i ) p i |
− m Y2 ; |
(7.6) |
||
|
|
|
|
|
i = 1 |
|
|
|
|
α k ( y ) = |
M |
[ Y k ] |
= ∑n |
ϕ k ( x i ) p i ; |
(7.7) |
||||
|
|
|
|
|
i |
= 1 |
|
|
|
|
o |
k |
|
n |
|
|
|
) k p i . |
|
µ k ( y ) = M [ Y |
] = |
|
∑ (ϕ ( x i ) − m Y |
(7.8) |
|||||
i = 1
Если Х – непрерывная случайная величина с известной плотностью вероятностей f(x), то формулы принимают вид
m Y = M [Y ] |
= |
+∞∫ ϕ ( x ) f ( x ) dx ; |
(7.9) |
|
|
|
|
− ∞ |
|
D Y = M [ Y 2 ] − m Y |
2 |
= |
+∞∫ ϕ 2 ( x ) f ( x ) dx − m Y2 ; |
(7.10) |
|
|
|
− ∞ |
|