
Лекции
.pdf
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ «МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ» ИНСТИТУТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
Курс лекций
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
7 семестр
Лектор Горицкий Юрий Александрович
Москва,2011

Лекция № 1.
ОСНОВНЫЕ ПОНЯТИЯ.
Математическая статистика – наука, дающая полезную информацию из наблюдений. Статистические задачи связаны с тем, что закон распределения неизвестен.
Пример |
|
|
|
|
|
|
|
|
|
|
Пусть – доля дефектных изделий. |
|
|
|
|
|
|||||
Из N изделий случайно выбираем одно изделие и смотрим на результат: |
||||||||||
|
|
|
{ |
1 (дефект), с вероятностью |
|
|
||||
|
|
|
0, с вероятностью |
1 |
|
|
||||
Продолжаем выбирать |
изделия |
, |
раз, |
|
1 |
|
||||
получаем случайные результаты: |
|
|
||||||||
|
|
|
|
|
||||||
|
( |
, |
, |
, |
) |
|
|
|
|
|
Все |
независимы и случайно распределены. |
|
|
|
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
1 |
Возникающие вопросы (типы задач): |
|
|
||||||
1. |
По выборке |
, |
, |
, |
оценить |
(теория точечного оценивания). |
||
|
̂ |
̂( , |
, |
, |
), |
̂ |
|
|
2. |
Указать диапазон для |
(теория интервального оценивания). |
||||||
|
̂( , |
, , |
) |
|
̂ |
̂ |
̂( , |
, , ), ̂, ̂ |
3. |
По выборке |
, |
|
, , |
ответить на вопрос: можно ли считать, что |
|||
|
неизвестное |
распределение обладает |
некоторым свойством (теория |
|||||
|
проверки математических гипотез) |
|
||||||
Пример
Пусть – доля дефектных изделий. Можно ли считать, что:
1)0,1
2) 0,1 |
0,2 |
3)0,1
А-13-08 | http://a1308.ru |
1 | С т р а н и ц а |
|

ТЕОРИЯ ТОЧНОГО ОЦЕНИВАНИЯ.
§1. Общие свойства оценок.
Определение |
|
|
|
|
|
|
|
|
||
Последовательность |
, |
, , |
независимых случайно распределённых по |
|||||||
закону |
( |
) случайных величин называется выборкой (выборкой объёма из |
||||||||
генеральной совокупности, распределённой по закону |
( |
)). |
|
|||||||
Определение |
|
|
|
|
|
|
|
|
||
Статистика – любая функция наблюдения. |
|
|
|
|
|
|||||
Например: |
∑ |
, |
∑ |
, |
. |
|
|
|
|
|
Рассмотрим выборку случайных величин |
, |
, |
, |
, распределённых по |
||||||
закону |
( |
| ), зависящего от случайного параметра |
, то есть |
( | ). |
||||||
Определение
Функция наблюдений ̂ ( , , , ), с помощью которой оценивается неизвестный параметр, называется оценкой или оценивающей функцией.
10. Характеристики качества оценок.
а) Несмещённость.
Определение |
|
|
|
|
|
|
|
|
|
|
Оценка ̂ |
( |
, |
, |
, |
) |
( |
) называется несмещённой, если |
|||
|
|
|
|
|
|
|
( |
) |
|
|
̂ |
( ) |
|
( |
, |
, |
, ) |
|
|
|
|
∫ ∫ ( , |
|
, , |
|
) |
( , |
, , |
| ) |
( ) |
||
( ) |
|
|
|
|
|
|
|
|
|
|
̂ |
( |
) |
|
|
|
|
|
|
|
|
Определение |
|
|
|
|
|
|
|
|
|
|
Оценка ̂ |
( |
, |
, |
, |
) |
( |
) называется несмещённой, если |
|||
|
|
|
|
|
|
|
( ( |
) |
) |
0 |
Определение |
|
|
|
|
|
|
|
|
|
|
Оценка ̂ |
( |
, |
, |
, |
) |
( |
) называется смещённой, если |
|||
|
|
|
|
|
|
|
( ) |
( |
) |
|
А-13-08 | http://a1308.ru |
2 | С т р а н и ц а |
|

б) Состоятельность. |
|
|
|
|
|
|
|
|
|||
Определение |
|
|
|
|
|
|
|
|
|
|
|
Оценка ̂ |
( |
, |
, |
, |
) |
( |
) называется состоятельной, если |
||||
|
|
|
|
|
|
( |
) |
|
, |
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
Определение |
|
|
|
|
|
|
|
|
|
|
|
Оценка ̂ |
( |
, |
, |
, |
) |
( |
) называется состоятельной, если |
||||
|
|
|
|
|
|
|
|
|
0, |
|
|
Признак состоятельности |
|
0, |
. |
|
|
||||||
в) Оптимальность. |
|
|
|
|
|
|
|
|
|||
, ( |
) |
|
- |
|
|
|
|
|
|
|
|
Определение |
|
|
|
|
|
|
|
|
|
|
|
Оценка |
|
( |
, |
, , |
) |
|
( |
) называется оптимальной, если |
|||
|
|
|
|
|
, |
( |
) |
|
- |
, ( ) |
- |
|
|
|
|
|
|
|
|
|
* |
+ |
|
Если оценка |
( ) несмещённая, то |
|
|
. |
|
||||||
Введём функцию штрафов: |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(̂, |
) |
( ( |
), ). |
|
|
Будем рассматривать среднее значение от штрафа. Введём функцию среднего
риска оценки |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
( |
) |
|
(̂, |
) |
( |
( ), |
) |
|
Определение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Оценка |
|
|
|
( |
, , , |
) |
( |
) называется оптимальной, если |
||||||||
|
|
|
|
|
|
|
|
|
( |
) |
|
( |
) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
+ |
|
|
20. Оценивание вероятностей моментов. |
|
|
|
|
||||||||||||
а) Оценка вероятности случайного события A. |
( |
) |
||||||||||||||
Пусть проведено |
независимых испытаний случайного события A. |
|||||||||||||||
– количество появления события A в |
испытаниях. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
, ) |
|
|
Рассмотрим для |
оценку |
̂ |
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||||
̂ |
1 |
|
|
|
|
|
|
̂несмещённая |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
А-13-08 | http://a1308.ru |
3 | С т р а н и ц а |
|
, ̂ - |
̂ |
1 |
(1 |
) |
0, |
̂состоятельна |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
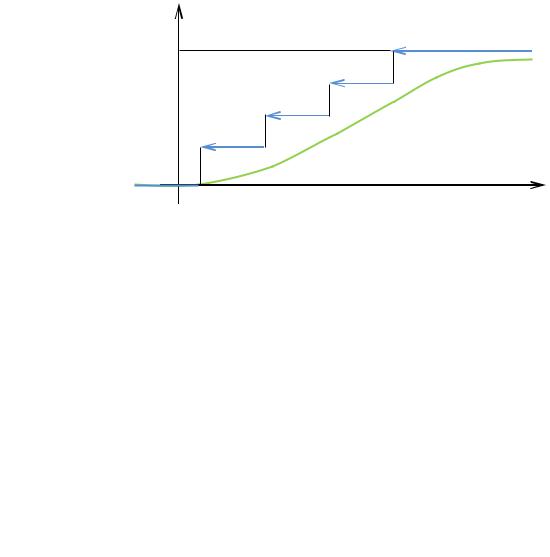
б) Оценка неизвестной функции распределения.
Рассматриваются |
|
независимых наблюдений случайной величины . |
|
|||||||||||||||||||
: |
, , |
|
, |
, |
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
– фиксировано. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
( ) |
* |
|
|
+ |
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
– количество появления события |
|
в |
испытаниях. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( , |
( )) |
|
|
|
|
|
|
|||
̂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
( |
) |
|
функция эмпирического распределения. |
|
|
|
|||||||||||
̂ |
|
|
|
|
1 |
|
|
|
̂ |
|
|
|
|
|
|
|
|
|
||||
( |
) |
|
|
|
|
|
|
|
( ) |
( ) |
( |
|
) несмещённая |
|
|
|
|
|||||
|
|
|
|
̂ |
|
|
|
̂ |
|
|
1 |
|
( )(1 |
( )) |
|
|||||||
|
[ |
( |
) |
( |
)] |
( |
) |
|
|
|
|
|
|
|
|
|
|
0, |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
̂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( |
) состоятельна |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
* ( ) |
( ), |
|
+ |
{ |
|
|
0 |
|
|
*| ( ) |
( )| |
+ 1} |
|||||||||
в) Оценка математического ожидания.
: , |
, , , |
|
|
( |
) |
|
|
|
||
|
|
|
|
∫ |
( ) |
|
|
|
||
̂ |
|
|
∫ |
|
|
( , |
̅, ̅, , ̅) |
1 |
∑ |
̅ выборочная средняя |
1 |
1 |
|
||||||||
̂ |
|
∑ |
|
̂ несмещённая |
||||||
|
|
|
|
|
||||||
А-13-08 | http://a1308.ru |
4 | С т р а н и ц а |
|

, ̂ |
- |
̂ |
[ |
1 |
∑ ] |
1 |
1 |
̅ 0, |
|
|
|
|
|
||||||
̂ состоятельная, если |
конечна. |
|
|
|
|
||||
А-13-08 | http://a1308.ru |
5 | С т р а н и ц а |
|

Лекция № 2.
ТЕОРИЯ ТОЧНОГО ОЦЕНИВАНИЯ (продолжение).
г) Оценивание неизвестной дисперсии . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
: |
|
|
, |
|
|
, |
, |
, |
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
∫ ( |
) |
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
( |
|
, |
|
|
, |
, |
, ) |
( |
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Оценка для математического ожидания: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
̂ |
|
|
1 |
∑ |
|
̅→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
̂ |
|
|
∫ ( |
̅ |
( ) |
∑( |
|
|
̅ |
|
|
̃ |
выборочная дисперсия |
|||||||||||||||||||
|
|
|
|
|
) |
|
|
|
|
) |
|
|
|
|||||||||||||||||||
Выполним преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
̃ |
|
1 |
∑( |
|
̅ |
1 |
∑[( |
|
|
|
) |
( |
̅ |
|
)] |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
∑( |
|
|
) 2( ̅ |
|
) |
1 |
∑( |
|
|
|
) ( ̅ ) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∑( |
|
|
) |
|
( ̅ |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
( |
|
|
|
|
|
|
) |
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( ̅ |
|
1 |
) |
|
( ̅ |
|
) |
|
|
|
̅ |
|
|
|
1 |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
̃ |
|
|
|
|
∑ |
( |
|
) |
|
|
( ̅ |
) |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
̃ |
|
смещённая для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рассмотрим другую оценку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
̃ |
1 |
|
|
|
|
|
|
̅ |
|
исправленная выборочная дисперсия |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 ∑( |
|
) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
несмещённая |
1 |
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
А-13-08 | http://a1308.ru |
6 | С т р а н и ц а |
||||
|
|||||

|
1 |
( |
3 |
) → 0 |
состоятельная, |
|
|
1 |
|||
|
|
|
|
|
|
где |
( |
) |
– -ый центральный момент. |
||
Теорема Хинчина |
|
|
Если |
, , , |
– последовательность независимых одинаково |
распределённых случайных величин, тогда для закона больших чисел
необходимо и достаточно существование математических ожиданий |
. |
|||||||||||||
|
|
|
|
|
|
|
|
{ БЧ: |
1 |
∑ |
, |
} |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим состоятельность выборочной дисперсии: |
|
|||||||||||||
̅ |
, |
|
|
,по теореме Хинчина- |
|
|
||||||||
1 |
∑( |
) |
, |
|
,по теореме Хинчина- |
|
|
|||||||
|
|
|
|
|||||||||||
̃ |
|
1 |
∑( |
|
) |
( ̅ |
) |
, |
|
|
||||
|
|
|
|
|
||||||||||
|
|
|
|
|
̃ |
|
, |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
д) Оценка моментов порядка |
2. |
|
|
|||||||||||
: |
, , , |
|
, |
( |
) |
|
|
|
|
|
||||
∫( )
̂1 ∑ (очевидно, что ср. арифметическое схоится к мат. ожиданию)
̂
̂ |
1 |
∑ |
, |
,по теореме Хинчина- |
|
|
|
∫ ( |
) |
( ) |
1 |
|
̅ |
|
|
|
|
|
|
|
̂ ∑( |
) |
, |
||
А-13-08 | http://a1308.ru |
7 | С т р а н и ц а |
|

Определение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность |
* |
+ |
сходится |
к |
0 |
по |
вероятности ( |
0 |
или |
||||||
* |
+ |
0), если |
|
0 *| |
| |
+ → |
1. |
|
|
|
|
|
|
||
Определение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность * |
+ сходится к 0 в средне квадратичном ( |
с.к. |
0 или |
||||||||||||
→ |
|||||||||||||||
|
0), если |
|
→ |
0. |
|
|
|
|
|
|
|
|
|
|
|
Определение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность * |
+ сходится к 0 почти наверное ( |
п.н. |
0 или |
|
|
0 с |
|||||||||
→ |
|
|
|||||||||||||
вероятностью 1), если вероятность случайного события |
* |
|
0+ |
1. |
|||||||||||
30. Свойства сходимости по вероятности: |
|
|
|
|
|
|
|
|
|||||||
1. |
Пусть |
и |
|
, тогда |
|
|
|
|
. |
|
|
|
|
|
|
2. |
Пусть |
и С |
|
с (числовая последовательность), |
|
|
|
|
|||||||
|
тогда |
| |
| |
|
. |
|
|
|
|
|
|
|
|
|
|
3. |
Пусть |
, тогда |
|
( |
) |
( |
), если |
непрерывна в точке . |
|
|
|||||
40. Линейная оценка (минимальная дисперсия среднего при различных наблюдениях).
, |
, |
, |
– независимые случайные величины; |
||||
, |
, |
, |
– независимые случайные величины. |
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̂ ∑
̂
̂ (∑ ) ∑( ) ∑
∑1 условие несмещённости.
А-13-08 | http://a1308.ru |
8 | С т р а н и ц а |
|

̂ (∑ ) ∑ |
|
* , , , + |
|
Получили задачу на условный экстремум. Для её решения необходимо построить функцию Лагранжа.
( , , , , ) |
∑ |
|
|
|
(∑ 1) |
|||
|
|
|||||||
2 |
с |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
2 |
|
||||
|
|
|
|
|
|
|||
Поставим условие
(∑ 1) 0,
тогда |
|
|
|
|
|
|
|
|
∑ |
1 |
(∑ ) |
|
|
|
̂ |
|
∑ |
|
Необходимо знать характеристику точности величины, то есть |
||||
дисперсию. |
|
|
|
|
|
̂ |
∑ |
|
(∑ |
) |
|
|
|
||||
А-13-08 | http://a1308.ru |
9 | С т р а н и ц а |
|
