Математические модели в точных и гуманитарных науках (Зайцев В

STIGAET KRITI^ESKOGO ZNA^ENIQ { PREDELA {<NBERGA-~ANDRASEKARA. pRI \TOM WNUTRENNIE SLOI ZWEZDY BYSTRO SVIMA@TSQ I RAZOGREWA@TSQ, NO RADIUS WSEJ ZWEZDY PRI \TOM UWELI^IWAETSQ. |TO PODTWERVDAETSQ RE[E-

NIEM MODELXNYH URAWNENIJ STROENIQ ZWEZDY S PEREMENNYM HIMI^ESKIM SOSTAWOM { ZWEZDA GLAWNOJ POSLEDOWATELXNOSTI (V) PREWRA]AETSQ W KRAS- NYJ GIGANT (III). sWETIMOSTX PRI \TOM PO^TI NE MENQETSQ.

pROWERKA ADEKWATNOSTI \TOJ MODELI MOVET PROWEDENA S POMO]X@ OB- RABOTKI NABL@DATELXNYH DANNYH. bOLX[OE ZNA^ENIE IME@T DIAGRAMMY gr, POSTROENNYE DLQ ZWEZD [AROWYH (\STAROE" NASELENIE TIPA II) I RASSE- QNNYH (\MOLODOE" NASELENIE TIPA I) ZWEZDNYH SKOPLENIJ. dELO W TOM, ^TO ZWEZDY L@BOGO SKOPLENIQ IME@T, KAK PRAWILO, OB]EE PROISHOVDENIE NA

PROTQVENII NEBOLX[OGO INTERWALA WREMENI I PRAKTI^ESKI ODINAKOWYJ ISHODNYJ HIMI^ESKIJ SOSTAW. pO\TOMU MOVNO S^ITATX, ^TO RAZLI^NOE POLOVENIE ZWEZD NA DIAGRAMME gr OBUSLOWLENO ISKL@^ITELXNO RAZLI^I- EM W NA^ALXNOJ MASSE. i DIAGRAMMY gr RAZLI^NYH ZWEZDNYH SKOPLENIJ OBLADA@T SLEDU@]IM OB]IM SWOJSTWOM { DO OPREDELENNOJ SWETIMOSTI (NA^INAQ S SAMYH SLABYH ZWEZD) ^ETKO PROSLEVIWAETSQ GLAWNAQ POSLEDO- WATELXNOSTX, A DLQ BOLEE QRKIH ZWEZD POLOVENIE ZWEZDY NA DIAGRAMME SME]AETSQ WPRAWO (RIS. 8). pOLOVENIE \TO^KI POWOROTA" K OBLASTI GI-

lg L L

2,0

0,0

-2,0

rIS. 8. dIAGRAMMA gr DLQ [AROWYH SKOPLENIJ

41

GANTOW ZAWISIT OT WOZRASTA SKOPLENIQ, A OTSUTSTWIE ZWEZD GLAWNOJ PO- SLEDOWATELXNOSTI WY[E TO^KI POWOROTA GOWORIT O TOM, ^TO ^EM QR^E (I MASSIWNEE) ZWEZDA, TEM BYSTREE ONA \WOL@CIONIRUET, T. E. TEM MENX[E WREMQ EE VIZNI. pO\TOMU KRAJNE NESOSTOQTELXNYMI WYGLQDQT POPYT- KI RASSMATRIWATX POGLO]ENIE ZWEZDOJ MEVZWEZDNOJ MATERII (NAPRIMER, PRI PROHOVDENII ^EREZ GAZOWU@ ILI PYLEWU@ TUMANNOSTX), KAK FAKTOR, PRODLEWA@]IJ VIZNX ZWEZDE.

dOSTIVENIE PREDELA {<NBERGA-~ANDRASEKARA SOPROWOVDAETSQ \WOZGO- RANIEM" GELIQ, REZULXTATOM ^EGO MOVET STATX WSPY[KA NOWOJ ILI OBRA- ZOWANIE PLANETARNOJ TUMANNOSTI. mOVET PROIZOJTI TAKVE WYBROS ^A- STI WE]ESTWA ZWEZDY ILI POLNOE PEREME[IWANIE. aNALOGI^NO, SOGLAS- NO DRUGIM GIPOTEZAM, OBRAZOWANIE PLANETARNYH TUMANNOSTEJ I DAVE WZRYWY SWERHNOWYH I TIPA QWLQETSQ REZULXTATOM WZRYWNOGO NA^ALA \WOZ- GORANIQ" UGLERODA. wSE \TI PROCESSY SU]ESTWENNO OSLOVNQ@T MODELI- ROWANIE \WOL@CII. k NASTOQ]EMU MOMENTU PROWEDENY MNOGO^ISLENNYE WY^ISLITELXNYE \KSPERIMENTY, MODELIRU@]IE RAZLI^NYE \WETWI" \WO- L@CII, SOOTWETSTWU@]IE NALI^I@ ILI OTSUTSTWI@ KONWEKCII, WYBROSA WE]ESTWA, SBROSA OBOLO^KI, PULXSACIQM ZA S^ET NEUSTOJ^IWOSTI K FL@K- TUACIQM I DR. w ^ASTNOSTI, PREDSTAWLQET INTERES GIPOTEZA, SOGLASNO KOTOROJ WZRYW SWERHNOWOJ I TIPA WYZYWAETSQ SPONTANNYM SINTEZOM IZO- TOPA Cf254 { EDINSTWENNOGO BOGATOGO NEJTRONAMI IZOTOPA, USTOJ^IWOGO

K- I -RASPADU. pERIOD WREMENI UMENX[ENIQ SWETIMOSTI SWERHNOWOJ W 2 RAZA { 55 DNEJ { UDIWITELXNO KORRELIRUET S PERIODOM POLURASPADA UKAZANNOGO IZOTOPA { 56; 2 0; 7 DNEJ.

wO WSQKOM SLU^AE QSNO, ^TO ZWEZDY MALOJ MASSY \WOL@CIONIRU@T, W OSNOWNOM, SOGLASNO PRIWEDENNYM WY[E RASSUVDENIQM. s^ITAETSQ, ^TO

ESLI MASSA ZWEZDY M < 1; 44M (M { MASSA sOLNCA), TO KONE^NYM REZULXTATOM \WOL@CII BUDET BELYJ KARLIK { ZWEZDA, SOSTOQ]AQ IZ WY-

ROVDENNOGO GAZA. pRI 1; 44M < M < 2M GRAWITACIONNOE SVATIE PRIWODIT K E]E BOLX[EMU UPLOTNENI@ WE]ESTWA ZWEZDY { OBRAZUETSQ NEJTRONNAQ ZWEZDA. eSLI VE ZWEZDA IMEET MASSU BOLX[E DWUH SOLNE^- NYH, STADIQ NEJTRONNOJ ZWEZDY OKAZYWAETSQ NEUSTOJ^IWOJ PO OTNO[ENI@

KDALXNEJ[EMU GRAWITACIONNOMU SVATI@, I, KAK TOLXKO RADIUS ZWEZ- DY STANOWITSQ RAWEN RADIUSU SFERY {WARC[ILXDA, ONA KOLLAPSIRUET I PREWRA]AETSQ W \^ERNU@ DYRU".

zWEZDY BOLX[OJ MASSY (M > 6M ), KAK PRAWILO, \NE DOVIWA@T" DO STADII GRAWITACIONNOGO KOLLAPSA { KAK TOLXKO WE]ESTWO CENTRALXNYH OBLASTEJ PREWRA]AETSQ W \LEMENTY GRUPPY VELEZA, QDERNYE REAKCII PREKRA]A@TSQ, NO TEMPERATURA W CENTRE PRODOLVAET WOZRASTATX. tEM- PERATURA NARUVNYH SLOEW, W KOTORYH IMEETSQ QDERNOE TOPLIWO, SILXNO UWELI^IWAETSQ, W REZULXTATE ^EGO PROISHODIT QDERNYJ WZRYW, RAZRU[A-

42

@]IJ ZWEZDU I PRIWODQ]IJ K WSPY[KE SWERHNOWOJ (II TIPA). pRI \TOM SINTEZIRU@TSQ TQVELYE \LEMENTY I WOZNIKA@T POTOKI KOSMI^ESKIH LU- ^EJ, A OSTATOK ZWEZDY MOVET STATX PULXSAROM. pRI^INOJ WSPY[EK NOWYH

ZWEZD MOVET BYTX BYSTRYJ OBMEN MASSOJ MEVDU KOMPONENTAMI TESNYH DWOJNYH SISTEM.

2.4.sIMMETRIQ KAK FUNDAMENTALXNOE SWOJSTWO

pOD SIMMETRIEJ MY PONIMAEM SWOJSTWO OSTAWATXSQ NEIZMENNYM (T. E. INWARIANTNYM) POD DEJSTWIEM NEKOTORYH PREOBRAZOWANIJ. sIM- METRIQ W TOJ ILI INOJ FORME PRISU]A WSEM REALXNYM OB_EKTAM, PO\TOMU

SIMMETRIJNYE SWOJSTWA ^ASTO OKAZYWA@TSQ OPREDELQ@]IMI FAKTORAMI KAK PRI POSTROENII MODELI, TAK I PRI PROWERKE EE NA ADEKWATNOSTX. bO- LEE TOGO, BOLX[INSTWO FUNDAMENTALXNYH ZAKONOW SAMI PO SEBE QWLQ@TSQ SIMMETRIQMI: NAPRIMER, L@BOJ ZAKON SOHRANENIQ, OPREDELQQ NEKOTORU@ SOHRANQ@]U@SQ WELI^INU, GARANTIRUET EE NEIZMENNOSTX, T. E. INWA- RIANTNOSTX, WO WSEJ OBLASTI SU]ESTWOWANIQ. w ^ASTNOSTI, TAKIM SWOJ- STWOM OBLADA@T PERWYE INTEGRALY DIFFERENCIALXNYH URAWNENIJ.

mATEMATI^ESKI SIMMETRIQ MOVET BYTX OPREDELENA KAK INWARIANT GRUPPY PREOBRAZOWANIJ. w PERENOSNOM SMYSLE SIMMETRIEJ NAZYWA@T SAMU GRUPPU PREOBRAZOWANIJ, I, ESLI ONA NEPRERYWNA, TO I SOOTWET- STWU@]IJ EJ INFINITEZIMALXNYJ OPERATOR, PREDSTAWLQ@]IJ SO- BOJ OPERATOR BESKONE^NO-MALOGO PREOBRAZOWANIQ, PRINADLEVA]EGO \TOJ GRUPPE. pO\TOMU I OBLASTX MATEMATI^ESKOGO ANALIZA, IZU^A@]AQ SIM- METRII RAZLI^NYH URAWNENIJ, NAZYWAETSQ GRUPPOWYM ANALIZOM. zA- METIM, ^TO W KLASSI^ESKOM GRUPPOWOM ANALIZE (WWEDENNYM W MATEMA- TI^ESKU@ PRAKTIKU W KONCE XIX WEKA sOFUSOM lI), RASSMATRIWA@TSQ NE STOLXKO \^ISTYE" INWARIANTY, SKOLXKO URAWNENIQ, INWARIANTNYE NA MNOGOOBRAZII SWOIH SOBSTWENNYH RE[ENIJ { DLQ MODELXNYH ZADA^ \TOGO, KAK PRAWILO, DOSTATO^NO (SM., NAPRIMER, [15]).

mODELXNYE URAWNENIQ, OPISYWA@]IE FUNDAMENTALXNYE ZAKONY, KAK PRAWILO, OBLADA@T WYSOKOJ SIMMETRIEJ (T.E. QWLQ@TSQ INWARIANTNY- MI OTNOSITELXNO NESKOLXKIH RAZLI^NYH GRUPP PREOBRAZOWANIJ). tAK, W PODAWLQ@]EE MNOVESTWO MODELXNYH URAWNENIJ NE WHODQT QWNO NI PRO- STRANSTWENNYE PEREMENNYE, NI WREMQ. pRI^INA PROSTA: FUNDAMENTALX- NYJ FIZI^ESKIJ ZAKON NE ZAWISIT OT WYBORA NA^ALA KOORDINAT, ON IN- WARIANTEN OTNOSITELXNO PROIZWOLXNYH SDWIGOW L@BYH NEZAWISIMYH PE- REMENNYH. kOSWENNO \TO OZNA^AET E]E I USTOJ^IWOSTX RE[ENIQ OTNO- SITELXNO RAZLI^NYH FL@KTUACIJ { PROIZWOLXNAQ TRANSLQCIQ PEREWODIT RE[ENIE SNOWA W RE[ENIE, T. E. FIZI^ESKAQ SU]NOSTX \SDWINUTOGO" RE[E- NIQ SOHRANQETSQ.

43

pROWERKA ADEKWATNOSTI MODELI S TO^KI ZRENIQ SOHRANENIQ SIMMETRII OPISYWAEMOGO REALXNOGO OB_EKTA MOVET PROIZWODITXSQ DWUMQ METODAMI:

A) POISKOM SIMMETRIJ POLU^ENNOGO MODELXNOGO URAWNENIQ, I

B) POSTROENIEM MODELXNOGO URAWNENIQ, UVE IME@]EGO APRIORNU@ SIM- METRI@ REALXNOGO OB_EKTA.

pERWYJ METOD PREDPOLAGAET RE[ENIE PRQMOJ ZADA^I GRUPPOWOGO ANALIZA DLQ POSTROENNOGO MODELXNOGO URAWNENIQ { PO ZADANNOMU URAWNE-

NI@ ILI KLASSU URAWNENIJ I]ETSQ DOPUSKAEMYJ IM INFINITEZIMALXNYJ OPERATOR NEPRERYWNOJ SIMMETRII, PERWYJ INTEGRAL ILI DISKRET- NAQ GRUPPA \KWIWALENTNOSTI. dALXNEJ[IM RAZWITIEM \TOGO METODA QW- LQETSQ POISK RE[ENIJ, INWARIANTNYH OTNOSITELXNO NAJDENNOJ SIMMET- RII { TAKIE INWARIANTNYE RE[ENIQ, KAK PRAWILO, IME@T DOSTATO^NO \PROZRA^NYJ" FIZI^ESKIJ SMYSL. dAVE ESLI \TO I NE TAK, POLU^ENNYE

W ZAMKNUTOJ FORME ANALITI^ESKIE RE[ENIQ MOGUT SLUVITX NULEWYMI PRIBLIVENIQMI ILI TESTAMI DLQ \FFEKTIWNOJ REALIZACII ^ISLENNYH ALGORITMOW.

dLQ PRIMENENIQ WTOROGO METODA NEOBHODIMO RE[ENIE OBRATNOJ ZADA^I GRUPPOWOGO ANALIZA { I]ETSQ KLASS URAWNENIJ, IME@]IJ APRI- ORNO ZADANNU@ SIMMETRI@. pRI TAKOM PODHODE L@BAQ POSTROENNAQ MO- DELX ZAWEDOMO BUDET IMETX TREBUEMU@ SIMMETRI@, I ZADA^A MODELIRO-

WANIQ SWODITSQ K PROBLEME WYBORA ISKOMOJ MODELI IZ [IROKOGO KLASSA URAWNENIJ. rE[ENIE OBRATNOJ ZADA^I PRIMENQETSQ TAKVE DLQ OPISANIQ WOZMOVNO BOLEE [IROKIH KLASSOW URAWNENIJ, INTEGRIRUEMYH W ZAMKNU- TOJ FORME, T.E. DLQ POISKA POTENCIALXNYH KLASSOW UDOBNYH MODELXNYH URAWNENIJ.

wAVNYMI ^ASTNYMI SLU^AQMI INWARIANTNYH RE[ENIJ QWLQ@TSQ AWTOMODELXNYE RE[ENIQ { RE[ENIQ, DOPUSKA@]IE (NERAWNOMERNOE) RAS- TQVENIE PO WSEM ZAWISIMYM I NEZAWISIMYM PEREMENNYM, WHODQ]IM W MO- DELXNOE URAWNENIE. iH WOSTREBOWANNOSTX W MODELIROWANII WOZNIKAET KAK SLEDSTWIE TOGO, ^TO PRAKTI^ESKI WSE FIZI^ESKI ZNA^IMYE IZMERQEMYE WELI^INY IME@T RAZMERNOSTX [16]. nAPRIMER, W SISTEME CGS RAZMER-

NOSTX WSEH FIZI^ESKIH WELI^IN IMEET WID STEPENNOGO ODNO^LE-

NA (MONOMA) LlM mT t. pOKAVEM, ^TO TAKOJ WID FORMULY RAZMERNOSTI OPREDELQETSQ SLEDU@]IM FIZI^ESKIM USLOWIEM: OTNO[ENIE DWUH ^ISLEN- NYH ZNA^ENIJ KAKOJ-NIBUDX PROIZWODNOJ WELI^INY NE DOLVNO ZAWISETX OT WYBORA MAS[TABOW DLQ OSNOWNYH EDINIC IZMERENIQ. dLQ OSNOWNYH

WELI^IN \TO USLOWIE QWLQETSQ SOSTAWNOJ ^ASTX@ OPREDELENIQ EDINICY IZMERENIQ I UDOWLETWORQETSQ SAMO SOBOJ.

pUSTX y { NEKOTORAQ RAZMERNAQ PROIZWODNAQ WELI^INA; DLQ PROSTO- TY PRIMEM SNA^ALA, ^TO ONA QWLQETSQ GEOMETRI^ESKOJ I PO\TOMU ZA-

44

WISIT TOLXKO OT DLIN, T.E. y = f (x1; x2; : : : ; xn). oBOZNA^IM SIMWO- LOM y0 ZNA^ENIE WELI^INY y, SOOTWETSTWU@]EE ZNA^ENIQM ARGUMENTOW x01; x02; : : : ; x0n. ~ISLOWOE ZNA^ENIE y, A TAKVE y0, ZAWISIT OT EDINICY IZMERENIQ DLQ RASSTOQNIJ x1; x2; : : : ; xn. uMENX[IM \TU EDINICU ILI MAS[TAB RASSTOQNIJ W RAZ. tOGDA SOGLASNO SFORMULIROWANNOMU WY[E

USLOWI@ MY DOLVNY IMETX

sLEDOWATELXNO, OTNO[ENIE ^ISLOWYH ZNA^ENIJ PROIZWODNYH GEOMETRI- ^ESKOJ WELI^INY, IZMERENNOJ W RAZLI^NYH MAS[TABAH DLINY, ZAWISIT TOLXKO OT OTNO[ENIQ MAS[TABOW DLIN. wID FUNKCII '( ) LEGKO NAHO- DITSQ { IZ

iNTEGRIRUQ, NAHODIM ' = C m. tAK KAK PRI = 1 IMEEM ' = 1, TO C = 1, T.E. ' = m. |TOT WYWOD SPRAWEDLIW DLQ L@BOJ RAZMERNOJ WELI^INY, ZAWISQ]EJ OT NESKOLXKIH OSNOWNYH WELI^IN, ESLI MY BUDEM MENQTX TOLXKO ODIN MAS[TAB. nETRUDNO WIDETX, ^TO W SLU^AE IZMENENIQ MAS[TABOW ; ; TREH OSNOWNYH WELI^IN, TO FUNKCIQ ' BUDET IMETX

45

WID ' = m n t. pO SU]ESTWU, \TO I OZNA^AET, ^TO RE[ENIE MODELXNOGO URAWNENIQ DOLVNO DOPUSKATX (NERAWNOMERNOE) RASTQVENIE.

fUNDAMENTALXNU@ ROLX SIMMETRII PODTWERVDAET I SRAWNENIE STROE- NIQ HIMI^ESKIH SOEDINENIJ I, NAPRIMER, KRISTALLOW. iZWESTNY HIMI^E- SKIE SOEDINENIQ S SAMOJ RAZNOOBRAZNOJ SIMMETRIEJ, TOGDA KAK KRISTAL- LOGRAFI^ESKIE GRUPPY SIMMETRII IME@T OBRAZU@]IE TOLXKO PORQDKA 2, 3, 4, 6. pROISHODIT \TO POTOMU, ^TO L@BAQ NEORGANI^ESKAQ KRISTAL-

LI^ESKAQ RE[ETKA DOLVNA DOPUSKATX GRUPPU LINEJNYH TRANS-

LQCIJ (DISKRETNYH PERENOSOW), A IZ GEOMETRII IZWESTNO, ^TO PRA- WILXNYE MOZAIKI POKRYWA@T PLOSKOSTX (BEZ ]ELEJ I NAKRYTIJ) TOLX- KO W SLU^AE, ESLI SOSTOQT IZ \LEMENTOW, IME@]IH DISKRETNYE GRUPPY WRA]ENIQ UKAZANNOGO PORQDKA. sEJ^AS, WPRO^EM, IZWESTNY MOZAIKI NA OSNOWE PRAWILXNOGO PQTIUGOLXNIKA (MOZAIKI pENROUZA) [17], ODNAKO ONI DOPUSKA@T SPIRALXNU@, A NE LINEJNU@ TRANSLQCI@, ^TO HARAKTERNO NE DLQ KRISTALLOW, A DLQ STRUKTUR VIWYH ORGANIZMOW (STROENIE SOCWETIJ, MORSKIH ZWEZD, RAKOWIN MOLL@SKOW I T.P.). aNALOGI^NO, FORMY REALX-

NYH KRISTALLOW MOGUT SOWPADATX TOLXKO S PERWYMI TREMQ PLATONOWYMI TELAMI { TETRA\DROM, KUBOM I OKTA\DROM, A TAKVE S IH KOMBINACIQMI. w LITERATURE ^ASTO WSTRE^AETSQ UTWERVDENIE, ^TO MNOGIE DRAGOCENNYE KAMNI (NAPRIMER, GRANATY) WSTRE^A@TSQ W PRIRODE W WIDE KRISTALLOW- DODEKA\DROW, ODNAKO IMEETSQ W WIDU NE PLATONOWO TELO { PENTAGONALXNYJ DODEKA\DR, A ROMBI^ESKIJ DODEKA\DR, WOOB]E NE QWLQ@]IJSQ PRAWILX- NYM MNOGOGRANNIKOM (ON DUALEN POLUPRAWILXNOMU POLI\DRU { KUBOOK- TA\DRU). ~TO VE KASAETSQ IKOSA\DRA, TO \TA FORMA [IROKO RASPROSTRA- NENA NA GRANICE \VIWOGO" I \MERTWOGO" { EE IME@T KAPSOMERY MNOGIH IZWESTNYH WIRUSOW, NEKOTORYE IZ NIH OBRAZU@T DAVE \KRISTALLY". wY- SKAZYWALASX ORIGINALXNAQ GIPOTEZA, ^TO SIMMETRII PORQDKA 5, 7 I BOLEE WYSOKIH PORQDKOW POQWILISX W VIWOJ PRIRODE KAK SREDSTWO WYVIWANIQ { ORGANIZMY, OBLADAW[IE BOLEE PROSTOJ SIMMETRIEJ, POGIBLI, ZAKRISTAL- LIZOWAW[ISX W PERESY]ENNOM SOLQNOM RASTWORE, KAKIM BYL, PO PREDPO- LOVENI@, \PERWOBYTNYJ OKEAN".

wERNEMSQ K STROENI@ HIMI^ESKIH WE]ESTW. hORO[O IZWESTNO, ^TO SO- STAW HIMI^ESKOJ MOLEKULY (STEHIOMETRIQ) ZAWISIT NE TOLXKO OT WALENT- NOSTI, NO I OT KOORDINACIONNOGO ^ISLA CENTRALXNOGO ATOMA. i ES- LI WALENTNOSTX OPREDELQETSQ SPOSOBNOSTX@ ATOMA OTDAWATX I PRISOEDI-

NQTX \LEKTRONY I QWLQETSQ FUNKCIEJ NOMERA \LEMENTA W PERIODI^ESKOJ SISTEME, BLIZKOJ K PERIODI^ESKOJ, TO KOORDINACIONNOE ^ISLO { FUNK- CIQ, BLIZKAQ K MONOTONNOJ, I OPREDELQETSQ GEOMETRI^ESKIMI PARAMET- RAMI CENTRALXNOGO IONA. gRUBO GOWORQ, KOORDINACIONNOE ^ISLO { KO- LI^ESTWO IONOW, KOTORYE MOGUT RAZMESTITXSQ W KOORDINACIONNOJ SFERE WOKRUG CENTRALXNOGO IONA.

46

rASSMOTRIM RQD KISLOT, OBRAZOWANNYH \LEMENTAMI GLAWNYH PODGRUPP 7-J, 6-J I 5-J GRUPP W WYS[EJ STEPENI OKISLENIQ:

NACIONNYE ^ISLA CENTRALXNYH ATOMOW RAWNY, SOOTWETSTWENNO, 3, 4 I 6. pERWYJ (NEPOLNYJ) STOLBEC WKL@^AET TOLXKO AZOTNU@ KISLOTU, KOTORAQ QWLQETSQ WESXMA SILXNOJ. sLEDUQ [ABLONNOJ ANALOGII, MOVNO BYLO BY OVIDATX, ^TO OSNOWNAQ FORMA FOSFORNOJ KISLOTY IMEET TAKOJ VE STE- HIOMETRI^ESKIJ SOSTAW, T. E. HPO3, NO \TO NE TAK! oRTOFOSFORNAQ KIS- LOTA TREHOSNOWNA (WTOROJ STOLBEC TRETXEJ STROKI) I PREDSTAWLQET SO- BOJ KISLOTU SREDNEJ SILY. sOEDINENIQ, FORMALXNO SOOTWETSTWU@]IE PO SOSTAWU AZOTNOJ KISLOTE (\METAFOSFORNAQ KISLOTA") IZWESTNY, NO PRED- STAWLQ@T SOBOJ POLIMERY [HPO3]n I IME@T CEPNOE ILI CIKLI^ESKOE STROENIE. tAKOE RAZLI^IE W STRUKTURE (I SWOJSTWAH!) OPREDELQETSQ KOOR- DINACIONNYM ^ISLOM, KOTOROE U AZOTA RAWNO TREM (PLOSKIJ RAWNOSTORON- NIJ ION NO3 ), A U FOSFORA (I U MY[XQKA) { ^ETYREM (TETRA\DRI^ESKIJ ION PO4 3). sOOTWETSTWU@]EE SOEDINENIE SURXMY SU]ESTWUET LI[X W WIDE \KRISTALLOGIDRATA" S DWUMQ MOLEKULAMI WODY, T. E. W FORME SEMIOSNOWNOJ O^ENX SLABOJ KISLOTY H7SbO6 (OKTA\DRI^ESKIJ ION SbO6 7). w LITERATURE OTME^AETSQ, ^TO \W DEJSTWITELXNOSTI NE ZAFIKSIROWANO NI ODNOGO SLU^AQ STRUKTURNOJ ANALOGII MEVDU SOOTWETSTWU@]IMI PROIZ- WODNYMI FOSFORA I SURXMY" [18].

pERWAQ I WTORAQ STROKI SOHRANQ@T \TU TENDENCI@ S TOJ LI[X RAZ- NICEJ, ^TO ANALOGA AZOTNOJ KISLOTE W NIH NET (KISLOROD I FTOR NE OB- RAZU@T KISLORODSODERVA]IH KISLOT I NE MOGUT NAHODITXSQ W WYS[EJ, SOOTWETSTWU@]EJ NOMERU GRUPPY, STEPENI OKISLENIQ). kROME \TOGO, KIS- LOTY S KOORDINACIONNYM ^ISLOM CENTRALXNOGO ATOMA, RAWNYM ^ETYREM, QWLQ@TSQ SILXNYMI (SERNAQ SRAWNIMA S AZOTNOJ, HLORNAQ VE WOOB]E S^I- TAETSQ ODNOJ IZ SAMYH SILXNYH KISLOT).

wLIQNIE KOORDINACIONNOGO ^ISLA, W SWO@ O^EREDX ZAWISQ]EGO OT RA- DIUSA CENTRALXNOGO IONA, OSOBENNO ZAMETNO W SRAWNENII S ZAKONOMERNYM

UWELI^ENIEM SILY GALOGENOWODORODNYH I HALXKOGENOWODORODNYH KISLOT I OSNOWANIJ ]ELO^NYH I ]ELO^NOZEMELXNYH METALLOW:

47

(W KWADRATNYH SKOBKAH { WODA, NE IME@]AQ WYRAVENNOGO KISLOTNOGO ILI ]ELO^NOGO HARAKTERA, I KRAJNE NESTABILXNYE PROIZWODNYE RADIOAKTIW- NYH \LEMENTOW).

w ZAKL@^ENIE \TOGO PARAGRAFA PRIWEDEM NESKOLXKO PRIMEROW STROE- NIQ MOLEKUL SOEDINENIJ S NESKOLXKO NEOBY^NYM KOORDINACIONNYM ^IS- LOM (5, 7, 9) [18]. kAK UKAZYWALOSX WY[E, OSI SIMMETRII TAKIH PORQDKOW NE WSTRE^A@TSQ W KRISTALLAH, NO NA OTDELXNYE MOLEKULY \TOT ZAKON NE RASPROSTRANQETSQ. tEM NE MENEE STRUKTURA L@BOGO HIMI^ESKOGO SO- EDINENIQ POD^INQETSQ OPREDELENNYM PRAWILAM. |TI PRAWILA DIKTU@TSQ RAWNOPRAWIEM (ILI NERAWNOPRAWIEM) IONOW W KOORDINACIONNOJ SFERE, A TAKVE NALI^IEM (ILI OTSUTSTWIEM) STROGOJ (ILI NESTROGOJ) CENTRALX- NOJ SIMMETRII. dLQ L@BOGO WYPUKLOGO MNOGOGRANNIKA SPRAWEDLIWA FOR-

MULA |JLERA

N0 + N2 = N1 + 2;

GDE N0 { ^ISLO WER[IN, N1 { ^ISLO REBER I N2 { ^ISLO GRANEJ. iZ \TOJ FORMULY SLEDU@T URAWNENIQ, OTNOSQ]IESQ K ^ASTNYM TIPAM POLI\DROW. eSLI W KAVDOJ WER[INE SHODQTSQ 3 REBRA (POLI\DR SO SWQZANNOSTX@ 3) I fn { ^ISLO GRANEJ S n REBRAMI (ILI WER[INAMI), TO

3f3 + 2f4 + f5 0f6 f7 2f8 = 12:

aNALOGI^NO, DLQ POLI\DROW SO SWQZANNOSTX@ WER[IN 4 I 5 URAWNENIQ

IME@T WID

2f3 0f4 2f5 4f6 = 16; f3 2f4 5f5 8f6 = 20:

eSLI POTREBOWATX, ^TOBY WSE GRANI POLI\DROW BYLI ODNOGO TIPA, TO MY POLU^AEM WSE PRAWILXNYE MNOGOGRANNIKI (PLATONOWY TELA). dALEE, ES- LI POSTROITX URAWNENIE DLQ POLI\DRA S 6-SWQZANNYMI WER[INAMI, TO KO\FFICIENT PRI f3 OKAZYWAETSQ RAWNYM NUL@, A WSE OSTALXNYE KO\F- FICIENTY OTRICATELXNY. sLEDOWATELXNO, NE SU]ESTWUET WYPUKLOGO MNO- GOGRANNIKA, W KOTOROM W KAVDOJ WER[INE SHODQTSQ 6 REBER. pO \TOJ VE PRI^INE NEWOZMOVNY I POLI\DRY, W KAVDOJ WER[INE KOTORYH SHODITSQ BOLEE [ESTI REBER.

tAKIM OBRAZOM, SU]ESTWU@T DOWOLXNO VESTKIE OGRANI^ENIQ NA STRUK- TURY HIMI^ESKIH WE]ESTW, ^TO I POZWOLQET MODELIROWATX STROENIE SO- EDINENIJ, ISHODQ IZ PRINCIPOW TOPOLOGII I DOPOLNITELXNOJ INFORMACII O HIMI^ESKIH SWOJSTWAH. nAPRIMER, ESLI POTREBOWATX, ^TOBY WSE IONY KOORDINACIONNOJ SFERY BYLI RAWNOPRAWNY, TO DLQ 5-KOORDINACIONNYH SOEDINENIJ WOZMOVNA LI[X TRIWIALXNAQ PLOSKAQ KONFIGURACIQ W WI- DE PRAWILXNOGO PQTIUGOLXNIKA. eSLI TREBOWANIE RAWNOPRAWIQ NEMNOGO OSLABITX, TO NAIBOLEE SIMMETRI^NOJ OKAZYWAETSQ KONFIGURACIQ TRIGO- NALXNOJ BIPIRAMIDY (PENTAHLORID SURXMY SbCl5).

48

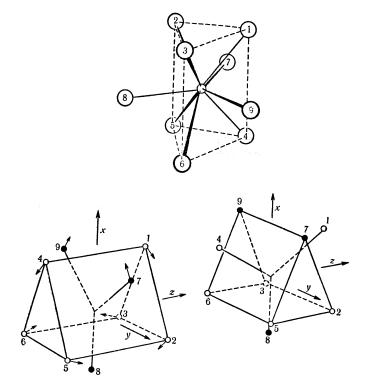
aNALOGI^NO, DLQ 7-KOORDINACIONNYH SOEDINENIJ ^ASTO WSTRE^AET- SQ KONFIGURACIQ PENTAGONALXNOJ BIPIRAMIDY (K3UF7; K3ZrF7), A 9- KOORDINACIONNYJ ION ReH9 2, PROBLEMY IDENTIFIKACII KOTOROGO IZ- LOVENY WY[E (SM. P. 1.6), IMEET STRUKTURU \TREH[APO^NOJ TRIGONALX- NOJ PRIZMY" (RIS. 9). w \TOM POLI\DRE K [ESTI WER[INAM TRIGONALX-

rIS. 9

NOJ PRIZMY DOBAWLQ@TSQ TRI \[APKI" { TRI WER[INY ^ETYREHGRANNYH PIRAMID, POSTROENNYH NA BOKOWYH GRANQH PRIZMY. pRI \TOM DOPOLNI- TELXNYE TRI ATOMA WODORODA NE \KWIWALENTNY OSTALXNYM [ESTI. tEM

NE MENEE TAKOJ KOMPLEKS MOVET DOWOLXNO LEGKO I OBRATIMO IZMENQTX KONFIGURACI@ ZA S^ET NEBOLX[IH DEFORMACIONNYH PEREME]ENIJ ATOMOW H, KAK POKAZANO NA RIS. 9 (WNIZU). w REZULXTATE \TOGO WSE 9 PROTONOW STANOWQTSQ \KWIWALENTNYMI S TO^KI ZRENIQ PROTONNOGO REZONANSA, ^TO I PODTWERVDAETSQ qmr-SPEKTROM [8].

w ZAKL@^ENIE PRIWEDEM E]E ODNU L@BOPYTNU@ ILL@STRACI@ PRINCI- PA EDINSTWA I MNOVESTWENNOSTI MODELEJ. nA RIS. 10 POKAZANA STRUKTURA SINTETI^ESKOGO CEOLITA RHO { TREHMERNAQ KUBI^ESKAQ RE[ETKA S USE- ^ENNYMI KUBOOKTA\DRAMI W UZLAH. w TO^NOSTI TAKOE VE STROENIE IMEET GRAF DISKRETNOJ GRUPPY PREOBRAZOWANIJ (C2 S4) C31 [19] PO PARA- METRAM , , GIPERGEOMETRI^ESKOGO URAWNENIQ gAUSSA

x(x 1)y00 + [( + + 1)x ]y0 + y = 0:

49

rIS. 10

2.5.|KOLOGI^ESKAQ MODELX: \HI]NIK { VERTWA"

rASSMOTRIM NEKOTORYJ WID VIWOTNYH, VIWU]IH IZOLIROWANNO W NEIZMENNOJ SREDE, ILI SOSU]ESTWU@]IH S DRUGIMI WIDAMI BEZ PRQMO- GO ILI KOSWENNOGO WLIQNIQ. pREDPOLOVIM, ^TO UKAZANNAQ SREDA SODER- VIT DOSTATO^NO KORMA. eSLI PRENEBRE^X PERIODI^NOSTX@ ROVDAEMOSTI I SMERTNOSTI, TO DLQ KOROTKOGO INTERWALA WREMENI ZADANNOJ DLINY W

DOSTATO^NO MNOGO^ISLENNOJ POPULQCII ^ISLO ROVDENIJ I ^ISLO SMERTEJ BUDUT PROPORCIONALXNY OB]EJ ^ISLENNOSTI INDIWIDUUMOW NA DANNYJ MOMENT. pRIROST ^ISLA INDIWIDUUMOW N W NEKOTOROM INTERWALE BUDET PROPORCIONALEN ^ISLU N , A TAKVE DLINE INTERWALA, POKA INTERWAL MAL:

dN = "N dt;

GDE " { KO\FFICIENT PRIROSTA. nETRUDNO WIDETX, ^TO ZDESX MY PUTEM OSREDNENIQ PERE[LI OT DISKRETNOJ MODELI K NEPRERYWNOJ, KAK BOLEE REALIZUEMOJ, TAK KAK W ITOGE MY POLU^AEM DIFFERENCIALXNOE URAWNENIE

PRI " = 0 WID POSTOQNEN (ROVDAEMOSTX KOMPENSIRUET SMERTNOSTX). eSLI WZAIMODEJSTWU@]IH WIDOW NESKOLXKO, NADO RASSMATRIWATX SISTEMU

1 dNi = f (N1; : : : ; Np); i = 1; : : : ; p: Ni dt

tAKOJ PODHOD K IZU^ENI@ BIOLOGI^ESKIH SOOB]ESTW BYL PREDLOVEN W 1926 GODU ITALXQNSKIM MATEMATIKOM wITO wOLXTERRA [20].

50