9. Отыскание оптимального решения основной задачи линейного программирования на основе табличного алгоритма замены переменных.

В задаче линейного программирования (ЛП) кроме уравнений-ограничений

существует ещё и линейная функция

которую нужно минимизировать.

Для нахождения опорного решения, обращающего в минимум линейную функцию, удобно воспользоваться табличным алгоритмом замены .

Для нахождения оптимального решения симплекс-методом необходимо чтобы оно удовлетворяла правилам:

1. Если все свободные члены (не считая строки L) в симплекс таблице неотрицательны, а в строке L (не считая свободного члена) нет ни одного положительного элемента, то оптимальное решение достигнуто.

2. Если в строке L есть положительный элемент, а в столбце, соответствующем ему, нет ни одного положительного элемента, то линейная функция L не ограничена снизу и оптимального решения не существует.

3. Если в этом столбце есть положительные элементы, то следует произвести замену одной из свободных переменных на одну из базисных, приём в качестве разрешающего надо взять тот элемент этого столбца, для которого отношение к нему соответствующего свободного члена минимально.

Рассмотрим пример:

Необходимо найти решение задачи ЛП с уравнениями:

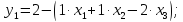
обращающее в минимум линейную функцию .

Решение:

Т.к. все свободные члены неотрицательны, то опорное решение:

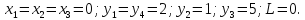
Это решение не оптимально, т.к. коэффициент при и положительны. Выберем , его надо поменять.

Составим таблицу:

Сначала рассчитываем значения, находящиеся на строке и столбце, которые мы меняем, а затем остальные ячейки в формулы для которых подставляем изначальные значения коэффициентов. В полученной таблице на основных строке и столбце тёмно-серым выделены новые коэффициенты.

Т.к. в строке L есть положительные элементы, то оптимальное решение не достигнуто.

Следует произвести замену одной из свободных переменных на одну из базисных.

- для строки ; - для строки ; По min выбираем .

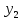Проводим аналогичные расчёты с заменой.

То же самое

Т.к. в строке L нет ни одного положительного элемента, то оптимальное решение достигнуто.

Ответ:

10. Метод динамического программирования (дп). Алгоритм решения задач управления состоянием организма в биотехнических системах. Основное рекуррентное уравнение дп.

Метод динамического программирования (ДП)

Рассмотрим управляемый процесс, который переводит некоторую систему G из начального состояния S₀ в конечное состояние S_m. При наличии промежуточных состояний такой перевод представляется в виде траектории, состоящей из конкретной последовательности промежуточных состояний (рис.2.1). Если промежуточные состояния могут быть различными, то траектория перевода G из S₀ в S_m неоднозначна и зависит от вырабатываемых управляющих воздействий x.

Введя какую-либо целевую функцию W = W(x), зависящую от выбранного управления x, можно сравнивать (по величине W) траектории друг с другом и ставить задачу об отыскании оптимальной траектории, при которой достигается экстремум W.

В зависимости от содержания целевой функции в процессе оптимизации ее стремятся либо максимизировать, либо минимизировать.

Будем рассматривать оптимизацию, при которой Wmin.

Задача заключается в отыскании оптимального управления x*, при котором целевая функция W достигает своего минимального значения W *, т.е.

Представим себе процесс управления, состоящий из конечного числа последовательных шагов. В этом случае траектория перехода G из S₀ в S_m будет иметь вид последовательности промежуточных состояний S₀, S₁, S₂…S_m, которая является результатом пошагового управления x, также имеющего вид последовательности x₀, x₁, x₂… x_m (обычно не числа, а вектора, функции, какие-либо предписания и т.п.). S_i обозначает состояние системы G, а x_i - управление на i-м шаге для произвольной траектории. Для конкретной же траектории конкретное управление x_i^’ переводит в конкретное состояние S_i^'.

Пусть на каждом отдельном i-м шаге, заключающемся в переходе из S_i-1 в S_i, известно значение целевой функции W которое обозначается w_i. Считая выбранный критерий аддитивным, т.е. полагая, что

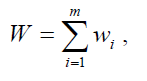
задача оптимизации формулируется следующим образом:

Требуется найти такое оптимальное управление x^* = x₀^*, x₁^*, x₂^*… x_m^* (x_i^*, где - оптимальное шаговое управление на i-м шаге), при котором целевая функция W принимает минимальное значение, т.е.

Последовательность оптимальный шаговых управлений x₁^*, x₂^*… x_m^* приводит к оптимальной траектории S₀, S₁, S₂…S_m перевода G из S₀ в S_m.

Рассмотрим пример, приведенный на рис.2.2.

Существует два варианта управлений и две возможных траектории, для каждой из которых можно подсчитать значение целевой функции.

Если W^’ > W^’’, то второй вариант является оптимальным, т.е.

x* = x^’’, W*= W^’’

• Поиск оптимального управления x* методом динамического программирования основан на использовании принципа оптимальности:

Каково бы ни было состояние S системы G в результате какого-то числа шагов, мы должны выбирать управление на ближайшем шаге так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к минимальному значению целевой функции на всех оставшихся шагах, включая данный.

После выбора способа описания состояний управляемой системы и разбиения всего процесса управления на шаги применяется следующая процедура:

1. Перечислить набор шаговых управлений x_i для каждого шага и налагаемые на них ограничения.

2. Для каждого i-го шага определить значение w_i в функции от состояния S_i-1 на -м шаге и от шагового управления x_i.

3. Определить, как изменяется состояние S_i-1 системы G под влиянием управления x_i на i-м шаге: оно переходит в новое состояние

4. Пусть W_i (S_i-1) - условный оптимум целевой функции, получаемый на всех последующих шагах, начиная с i-го и до конца. Надо записать основное рекуррентное уравнение динамического программирования, выражающее W_i (S_i-1) через уже известную функцию W_i+1 (S_i)

Этому условному оптимуму целевой функции W_i (S_i-1) соответствует условное оптимальное управление на i-м шаге x_i (S_i-1), которое совместно с оптимальным управлением на всех последующих шагах обращает целевую функцию на всех оставшихся шагах, начиная с данного, в минимум.

5. Произвести условную оптимизацию последнего (m-го) шага, задаваясь множеством состояний S_m-1, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого S_m-1 условный оптимум целевой функции по формуле

и находя условное оптимальное управление x_m (S_m-1), для которого этот минимум достигается.

6. Произвести условную оптимизацию (m-1)-го, (m-2)-го и т.д. шагов по формуле:

полагая в ней i = (m-1), (m-2),… и для каждого из шагов указать условное оптимальное управление x_i(S_i-1),при котором достигается минимум.

Так как начальное состояние системы S₀ одно, и оно известно, то на первом шаге варьировать состояние системы не нужно, оптимальное значение целевой функции для S₀ находится непосредственно.

Это и есть оптимум функции цели за весь процесс перевода:

W^* = W₁(S₀)

7. Произвести безусловную оптимизацию управления, учитывая выработанные ранее рекомендации на каждом шаге. На первом шаге оптимальное шаговое управление x₁^*= x₁(S₀),. Пользуясь (2.1), находим изменившееся состояние системы S₁, для него определяем оптимальное управление на втором шаге x₂^* и т.д. до конца.