8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.

При отыскании опорного решения попутно выясняется, имеет ли вообще данная задача допустимые (неотрицательные) решения.

Пусть имеется ОЗЛП (осн. задача лин. програм.) с ограничениями-равенствами, в следующей форме:

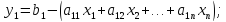
• Первое пробное решение x₁ = x₂ = ... = x_n = 0. Если все b_i ³ 0, то это допустимое решение, следовательно, оно опорное.

Если какие-либо b_i < 0, то это решение не допустимое и не опорное.

• Для нахождения ОР нужно шаг за шагом обменивать базисные и свободные переменные, пока не найдем его, либо убедимся, что система уравнений несовместима с неравенствами x₁ ³ 0, x₂ ³ 0,..., x_n ³ 0; y₁ ³ 0, y₂ ³ 0,..., y_m ³ 0.

Очевидно, нужно так обменивать базисные переменные со свободными, чтобы эта процедура приближала нас к границе ОДР, т.е. чтобы число отрицательных свободных членов уменьшалось или при том же числе убывали их абсолютные величины.

Способ выбора разрешающего элемента для приближения к опорному решению

Пусть имеется одно из уравнений с отрицательным свободным членом.

Ищем в этой строке отрицательный a_ij. Если они все положительные (значит все a_ij < 0)) и данная базисная никогда не будет положительной.

Выберем столбец, в котором находится отрицательный a_ij, в качестве разрешающего столбца.

Рассмотрим только те элементы столбца, которые имеют один знак со свободным членом.

Выберем из них тот в качестве разрешающего элемента, для которого отношение к нему свободного члена минимально (свободный член/коэффициент при x)

ПРИМЕР: (найти опорное решение задачи ЛП)

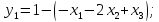
(элементы записываем не по строкам, а по столбцам!)

	Св. член	x1 , x1 « y3	x2	x3
y1	1 2	-1 1	-2 1	1 0
y2	-5 4	-2 2	1 2	-1 0
y3 , y3 « x1	2 2	1 λ=1	1 1	0 0
y4	1 0	0 0	-1 0	1 0

Видим, что есть отрицательный свободный член (-5) – это плохо. Значит нужно производить замену. Выберем разрешающий элемент:

Выберем столбец, в котором находится отрицательный a_ij, в качестве разрешающего столбца. Рассмотрим только те элементы столбца, которые имеют один знак со свободным членом.

Выберем из них тот в качестве разрешающего элемента, для которого отношение к нему свободного члена минимально (свободный член/коэффициент при x).

_{Произведем замену} y₃ « x_1.

_{Получаем:}

	Св. член	y3	x2	x3 , x3 « y2
y1	3 -1	1 2	-1 3	1 1
y2 , y2 « x3	-1 1	2 -2	3 -3	-1 λ= -1
x1	2 0	1 0	1 0	0 0
y4	1 -1	0 2	-1 3	1 1

Видим, что есть отрицательный свободный член (-1) – это плохо. Значит нужно производить замену. Выберем разрешающий элемент:

Проводим аналогичные действия.

Минимум для строк y2 и y4. Из них можно выбрать любой.

_{Производим замену} y₂ « x_3.

_{Получаем:}

	Св. член	y3	x2	y2
y1	2	3	2	1
x3	1	-2	-3	-1
x1	2	1	1	0
y4	0	2	2	1

Опорное решение найдено (т.к. все свободные члены неотрицательны):

y₃ = x₂ = y₂ = 0; y₁ = 2; x₃ =1; x₁ = 2; y₄ = 0.