15. Решение игры в смешанных стратегиях.

Задача теории игр – нахождение оптимальных стратегий игроков в предположении одинаковой «разумности» противников.

Рассмотрим игру (модель конфликтной ситуации), в которой участвует два игрока A и B, имеющие прямо противоположные интересы.

Процесс игры заключается в последовательных ходах (личных – сознательных и случайных) противников, а совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации называется стратегией игрока.

При конечном числе стратегий игра будет конечной. Пусть у игрока A имеется m возможных стратегий A₁, A₂…A_m, а у игрока B – n возможных стратегий B₁, B₂…B_n. Пусть также известны величины a_ij – выигрыши игрока A при использовании A_i с его стороны и B_i со стороны противника.

Тогда игра, называемая игрой m×n, может быть представлена таблицей, называемой платежной матрицей или просто матрицей игры.

По матрице игры определяются нижняя α и верхняя β цены игры.

Принцип выбора противниками стратегий, соответствующих получению ими выигрышей α и β называется принципом минимакса, а сами стратегии – минимаксными. Известно, что минимаксные стратегии устойчивы по отношению к информации о поведении другой стороны только в случае, если α = β.

В случае α ≠ β для получения наибольшего выигрыша игроку выгодно применять не одну (чистую) стратегию, а чередовать случайным образом несколько стратегий.

Такие стратегии, состоящие в случайном чередовании чистых стратегий, называются смешанными и задаются соответствующими вероятностными векторами.

Пусть S_A - смешанная стратегия игрока A, а S_B - смешанная стратегия игрока B. Тогда S_A =(p₁, p₂… p_m), S_B =(q₁, q₂… q_n), где p_i - вероятность применения игроком A стратегии A_i, q_i - вероятность применения игроком B стратегии B_i, причем

Чистая стратегия – частный случай смешанной.

Если допустить применение смешанных стратегий, то для каждой конечной игры можно найти хотя бы одно решение, т.е. пару устойчивых оптимальных стратегий игроков (S_A^*, S_B^*), обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступить от своей.

Выигрыш, соответствующий решению, называется ценой игры и в общем случае (при применении смешанной стратегии) лежит в интервале α ≤ γ ≤ β.

α – нижняя цена игры

γ – выигрыш

β – верхняя цена игры

Рассмотрим игру 2×2.

Ее матрица имеет вид:

Если в матрице 2×2 седловой точки нет и α ≠ β, то необходимо искать решение в смешанных стратегиях.

Пара оптимальных смешанных стратегий S_A = (p₁, p₂), S_B = (q₁, q₂), и цена игры в этом случае определяются по формулам:

Игра 2×2 и ее решение имеют простую геометрическую интерпретацию.

Пусть точки A₁ и A₂ соответствуют применению одноименных стратегий, а любая точка внутри этого отрезка соответствует некоторой смешанной стратегии S_A ^*= (p₁, p₂).

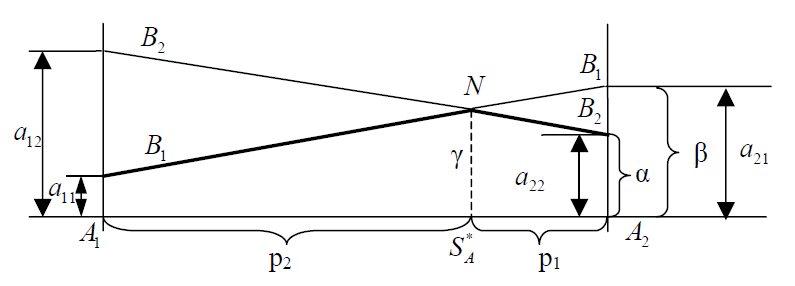
Рисунок 1 – геометрическая интерпретация задачи 2×2

Ординаты прямой B₁B₁, проведенной так, как показано на рис.1, соответствуют выигрышу игрока A при применении им любой стратегии (чистой или смешанной) при условии, что B применяет B₁. Прямая B₂B₂ также отражает выигрыш игрока A в случае, когда B применяет B₂. Жирной линией отмечена нижняя граница выигрыша B₁NB₂ – минимальный выигрыш игрока A при любой его смешанной стратегией. Очевидно, решение достигается в точке максимума нижней границы (на рис.1 в точке N). Геометрические построения легко осуществляются по элементам матрицы игры, которые откладываются на вертикальных осях.

По рисунку легко находятся α, β, γ и проводится анализ игры.

Геометрическим способом также легко анализируются и решаются игры 2×n.

Они задаются матрицей игры:

Например, геометрическая интерпретация игры 2×4, в которой число наклонных линий получается равным 4, по числу стратегий игрока B. имеет вид:

Рисунок 2 – геометрическая интерпретация задачи 2×4

Нижняя граница игры может в данном случае уже представлять сложную ломаную линию, максимум которой, как и ранее, определяет решения игры.

Т.е. находим, самую нижнюю кривую и самая верхняя точка пересечения в этой кривой и есть решение игры.

Из рис. 2 видно, что нижняя граница выигрыша – прямая B₁MNB₂, ее максимум достигается в точке N, которая определяет оптимальную стратегию S_A ^*= (p₁, p₂). Следует отметить, что стратегия B₃ вообще может не рассматриваться как заведомо невыгодная игроку B, а значения p₁ и p₂ можно найти по формулам игры 2×2, учитывая, что в точке N активных стратегий игрока B только две B₂ и B₄.