18. Решение игр 2хn

Пусть мы располагаем двумя стратегиями А₁, А_2, а противник – n стратегиями: В₁, В₂ …В_n. Матрица || a_ij || состоит из двух строк и n столбцов. Аналогично случаю двух стратегий дадим задаче геометрическую интерпретацию: n стратегий противника изобразятся n прямыми.

Строим нижнюю границу выигрыша (ломаную В₁MN В₂) и находим на ней точку N с максимальной ординатой.

Эта точка дает решение игры (стратегию):

ордината точки N равна цене игры, а абсцисса равна частоте стратегии

_{В данном случае (см. рисунок) оптимальная стратегия противника получается применением смеси двух «полезных» стратегий:} В_{1 и} В_{4, пересекающихся в точке N.}

Стратегия B3 является заведомо невыгодной, а стратегия B1 – невыгодной при оптимальной стратегии . Если А будет придерживаться своей оптимальной стратегии, то выигрыш не изменится, какой бы из своих «полезных» стратегий ни пользовался В, однако, он изменится, если В перейдет к стратегиям B1 или B3.

В теории игр доказывается, что у любой конечной игры mn имеется решение, в котором число «полезных» стратегий той и другой стороны не превосходит наименьшего из двух чисел m и n. В частности, из этого следует, что у игры 2n всегда имеется решение, в котором с той и другой стороны участвует не более двух «полезных» стратегий.

Пользуясь геометрической интерпретацией, можно дать простой способ решения любой игры 2n. Непосредственно по чертежу находим пару «полезных» стратегий противника Bj и Bk, пересекающиеся в точке N (если в точке N пересекается более двух стратегий, берем любые две из них). Мы знаем, что если игрок А придерживается своей оптимальной стратегии, то выигрыш не зависит от того, в какой пропорции применяет В свои «полезные» стратегии, следовательно,

Из этих уравнений и условия , находим и и цену игры v (В методе цена игры обозначается, как ).

Зная стратегию игры, можно сразу определить оптимальную стратегию игрока В:

Для этого решается, например, уравнение:

ДРУГОЙ ПРИМЕР (БОЛЕЕ ПОНЯТНЫЙ)

Любая конечная игра mn имеет решение, в котором число активных стратегий каждого игрока не превосходит L, где L = min (m, n)

У игры 2n или m2 всегда имеется решение, содержащее не более двух активных стратегий у каждого из игроков (min(2, n)=min(m,2)=2).

Пусть платежная матрица игры имеет вид:

Согласно теореме об активных стратегиях, решение находится из уравнения:

Найти максимум (по р) функции:

Для этого необходимо построить n прямых вида:

На плоскости (p,, p[0,1] и путем визуального сравнения выбрать ломанную, огибающую их снизу

Пример:

Матричная игра 2n задана следующей матрицей:

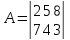
Найти: решение игры графическим и аналитическим методом.

Решение:

Сначала необходимо определит, решается ли данная игра в чистых стратегиях, то есть существует ли седловая точка или нет.

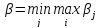
Вычисляя, получим:

Цена игры

Так как , то игра имеет седловой точки, и поэтому имеет решение в смешанных стратегиях.

Строим графическое изображение игры:

Находим точку оптимума – О. В этой точке пересекаются стратегии игру 22 с платежной матрицей вида:

Используя алгебраический метод решения этой игры, получаем точное решение:

Ответ: оптимальные смешанные стратегии игроков при цене игры