- •Оглавление
- •Методы принятия оптимальных решений. Математические модели операции: детерминированный случай, оптимизация решений в условиях неопределенности.
- •Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
- •Оценка операции по нескольким показателям эффективности
- •Основная задача линейного программирования (озлп). Допустимые решения и оптимальное решение задачи лп.
- •Геометрическая интерпретация озлп.
- •Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
- •6. Симплекс-метод решения задачи лп
- •7. Табличный алгоритм замены переменных.
- •8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
- •9. Отыскание оптимального решения основной задачи линейного программирования на основе табличного алгоритма замены переменных.
- •10. Метод динамического программирования (дп). Алгоритм решения задач управления состоянием организма в биотехнических системах. Основное рекуррентное уравнение дп.
- •11. Управление переходом организма из исходного в конечное состояние методом дп: использование ориентированного графа.
- •12. Управление переходом организма из исходного в конечное состояние в условиях неопределенности.
- •13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
- •14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
- •15. Решение игры в смешанных стратегиях.
- •16. Игры 2х2 и их решение.
- •17. Геометрическая интерпретация решений игры 2х2.
- •18. Решение игр 2хn
- •19. Решение игр mx2
- •20. Решение игр mxn.
-
Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
Оценка операции по нескольким показателям
Пусть есть несколько показателей эффективности W1, W2,…Wk
некоторые максимизируются, другие минимизируются
достижения максималного эффекта при минимуме затрат НЕКОРРЕКТНО
ПРАВИЛЬНО: достижения максимума эффективности при заданных затратах или наоборот
-
отбрасывание заведомо плохих вариантов
пусть операция оценивается по 2 показателям

-
использование составных критериев
U=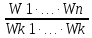 Wi ->max, Wk ->min
Wi ->max, Wk ->min
не хорошо т. к. недостаток одного можно компенсировать другим показателем
-
составной критерий
U=a1W1+a2W2+…+akWk (взвешенная сумма)
ai> 0, если Wi ->max
ai <0, если Wi -> min
ai коффициенты, которые связаны со степенью важности каждого веса
-
сведение к одному показателю с некоторыми ограничениями
многоэтапная процедура самый важный показатель впереди (ранжирование) нахождение максимума первого показателя при ограничениях на остальных

Любая
задача линейного программирования (ЛП)
может быть сведена к его основной задаче,
формулируемой математически следующим
образом. Имеется ряд
переменных
![]() .Требуется
найти
такие
неотрицательные
значения этих переменных, которые бы
удовлетворяли системе линейных уравнений:
.Требуется
найти
такие
неотрицательные
значения этих переменных, которые бы
удовлетворяли системе линейных уравнений:


……………………………………….
 (1.1)
(1.1)
и, кроме того, обращали бы в минимум линейную функцию
 (1.2)
(1.2)
Где
 заданные
постоянные
коэффициенты.
заданные
постоянные
коэффициенты.
Допустимым решением основной задачи ЛП называют любую совокупность переменных

удовлетворяющую уравнениям (1.1).
Оптимальным решением называется то из допустимых решений, при котором линейная функция (1.2) обращается в минимум.
Наконец, может оказаться, что допустимые решения основной задачи ЛП существуют, но среди них нет оптимального: функция L в области допустимых решений не ограничена снизу.
Матрицей
системы
линейных уравнений (1.1) называется
таблица, составленная из коэффициентов
при

|
|
|
… |
|
|
|
|
… |
|
|
… |
|
|
|
|
|
|
… |
|
Расширенной матрицей системы линейных уравнений называется та же матрица, дополненная столбцом свободных членов:
Структура задачи линейного программирования существенно зависит от ранга системы ограничений (1.1). Рассмотрим прежде всего случай, когда r=n, т. е. когда число линейно независимых уравнений, входящих в систему (1.1), равно числу переменных n. Если отбросить уравнения, являющиеся линейными комбинациями других, система уравнений-ограничений основной задачи ЛП принимает вид

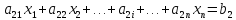


(1.3)
Так как r = n, то определитель, составленный из коэффициентов,
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
|
|
|
… |
|
Если
среди этих решений нет ни одного, для
которого все
 неотрицательны, это значит, что основная
задача ЛП не имеет допустимого, а
следовательно, оптимального решения.
неотрицательны, это значит, что основная
задача ЛП не имеет допустимого, а
следовательно, оптимального решения.
Если же существуют какие-то решения системы (1.1), для которых все

неотрицательны,
то каждое из них допустимо. Возникает
задача – найти среди допустимых решений
оптимальное,
т. е. такое решение
 для которого линейная функция (1.2)
обращается в минимум.
для которого линейная функция (1.2)
обращается в минимум.
На практике ограничения в задаче ЛП часто задаются не уравнениями, а неравенствами. Рассмотрим, как можно перейти от задачи с ограничениями-неравенствами к основной задаче ЛП.
Пусть
имеется задача
ЛП
с
n
переменными
 в которой ограничения, наложенные на
эти переменные, имеют вид линейных
неравенств.
В некоторых из них знак неравенства
может быть
,
в других
(второй вид сводится к первому переменой
знака в обеих частях неравенства).
Поэтому зададим все ограничения-неравенства
в стандартной форме:
в которой ограничения, наложенные на
эти переменные, имеют вид линейных
неравенств.
В некоторых из них знак неравенства
может быть
,
в других
(второй вид сводится к первому переменой
знака в обеих частях неравенства).
Поэтому зададим все ограничения-неравенства
в стандартной форме:





Будем
считать, что все эти неравенства линейно
независимы. Требуется найти такую
совокупность неотрицательных значений
 которая удовлетворяла бы неравенствам
(1.4), и, кроме того, обращала бы в минимум
линейную функцию
которая удовлетворяла бы неравенствам
(1.4), и, кроме того, обращала бы в минимум
линейную функцию

От задачи, поставленной таким образом, легко перейти к основной задаче ЛП. Введем обозначения:
 ;
;
 ;
;

 ,
,

Где
 – некоторые новые переменные, которые
принято называть добавочными. Согласно
условиям (1.4), эти добавочные переменные
так же, как и
– некоторые новые переменные, которые
принято называть добавочными. Согласно
условиям (1.4), эти добавочные переменные
так же, как и
 ,
должны быть неотрицательными.
,
должны быть неотрицательными.
Таким
образом, возникает задача линейного
программирования в следующей постановке:
найти такие неотрицательные значения
n
+ m
переменных
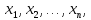 ;
;
 чтобы они удовлетворяли системе уравнений
(1.5) и одновременно обращали в минимум
линейную функцию этих переменных
чтобы они удовлетворяли системе уравнений
(1.5) и одновременно обращали в минимум
линейную функцию этих переменных

Рассмотрим
работу
станции скорой помощи. Известно,
что
имеется
n
классов
больных
(травматические,
кардиологические, ожоговые
и
т.
д.)
![]() Число вызовов (в день) по классу больных
Число вызовов (в день) по классу больных
 равно
равно
 . На станции имеется m
групп передвижных бригад скорой помощи
(общего типа, кардиологические и т. д.)
A1,
A2
,…, Am.
Группа
. На станции имеется m
групп передвижных бригад скорой помощи
(общего типа, кардиологические и т. д.)
A1,
A2
,…, Am.
Группа
 насчитывает
насчитывает
 бригад (и столько же машин). Выезд бригады
из группы
бригад (и столько же машин). Выезд бригады
из группы
 к больному класса
к больному класса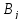 обеспечивает эффективность обслуживания
этого больного, равную
обеспечивает эффективность обслуживания
этого больного, равную
 .
Предполагается, что каждая бригада
может в день обслужить N
вызовов. Кроме того,
считается,
что общее число выездов
точно
совпадает
с
числом
вызовов, т.
е.
.
Предполагается, что каждая бригада
может в день обслужить N
вызовов. Кроме того,
считается,
что общее число выездов
точно
совпадает
с
числом
вызовов, т.
е.
 или
или
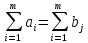 ,
,
где

Спрашивается,
сколько вызовов от каждого типа больных
должна об
служить
каждая
группа
этих
бригад
 .
чтобы суммарная эффективность обслуживания
L,
подсчитываемая по формуле
.
чтобы суммарная эффективность обслуживания
L,
подсчитываемая по формуле
 ,
(1.6) была
максимальна?
,
(1.6) была
максимальна?
Это транспортная задача ЛП. Математически она формулируется как максимизация L (или минимизация L L) при ограничениях
 ,
,
 (1.7)
(1.7)
 ,
,

 (1.8)
(1.8)
С целью достижения лучшего соответствия реальным условиям данная задача может быть усложнена, если равенства (1.7) и (1.8) заменить соответствующими неравенствами.
К задаче сводятся разнообразные распределительные задачи: распределение врачей разной специальности по разным группам больных в условиях массового заболевания, распределение ограниченного количества нескольких лекарственных препаратов по различным группам больных, распределение операторов по рабочим местам, распределение работ при трудотерапии психических больных по результатам их психофизиологического тестирования и др.