12. Управление переходом организма из исходного в конечное состояние в условиях неопределенности.

Поведение системы зависит не только от начального состояния S₀ и выбранного управления x, но и от случайности.

Рассмотрим стохастическую модель задачи о кратчайшем пути на ациклической сети. Допустим существование в системе условных вероятностей P(S_i/S_i-1) того, что на i-м шаге управления система перейдет в состояние S_i при условии, что до этого она находилась в S_i‑1 и было применено управление x_i. Это условие представляет собой допущение о марковском свойстве системы, согласно которому вероятность перехода системы в какое-либо состояние S_i зависит только от состояния S_i-1, из которого совершается переход, и от применяемого управления x_i, но никак не зависит от предыстории системы, предшествующей ее переходу в S_i-1.

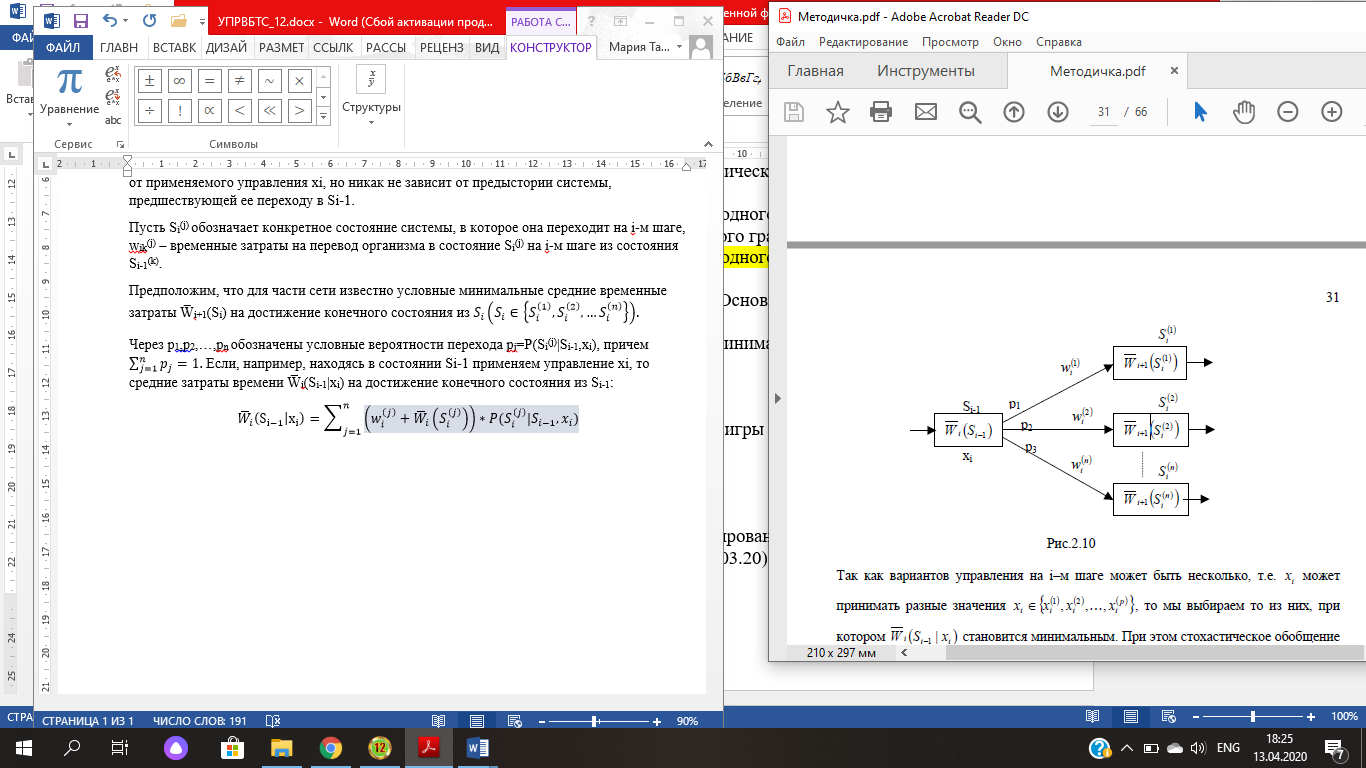
Пусть S_i^(j) обозначает конкретное состояние системы, в которое она переходит на i-м шаге, w_ik^(j) – временные затраты на перевод организма в состояние S_i^(j) на i-м шаге из состояния S_i-1^(k).

Предположим, что для части сети известно условные минимальные средние временные затраты W̅_i+1(S_i) на достижение конечного состояния из

Через р₁,р₂,…,p_n обозначены условные вероятности перехода p_j=P(S_i^(j)|S_i-1,x_i), причем Если, например, находясь в состоянии S_i-1 применяем управление x_i, то средние затраты времени W̅_i(S_i-1|x_i) на достижение конечного состояния из S_i-1:

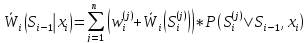
Т.к. вариантов управления на i-м шаге может быть несколько, т.е. x_i может принимать разные значения при котором становится минимальным. При этом стохастическое обобщение основного рекуррентного имеет вид:

Развернутая форма:

Т.к. мы применяем условные вероятности, то

Пример 1:

Решается задача управляемого перевода организма из исходного состояния S0 в конечное состояние S₃ (лечение, нормализация состояния оператора). При этом существуют промежуточные состояния , а возможные переходы их состояния в состояние изображены на рис.2.11 в виде ориентированного ациклического графа. На ребрах графа проставлено время, требуемое для перевода организма из одного состояния в другое. В каждом состоянии S_i-1 имеется несколько управляющих воздействий xi, которым соответствуют определенные наборы вероятностей перехода

Сумма чисел в каждой строке = 1

Кроме того, в состоянии всегда применяется управление x₃⁽¹⁾ и , а в состоянии всегда применяется x₃⁽²⁾ и

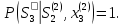
Требуется каждому состоянию сопоставить одно оптимальное управляющее воздействие, при котором общее среднее время перехода из в будет минимально, а также определить это время.

Времена перехода организма из состояния в состояние равны:

Условную оптимизацию, как и раньше, начинаем с последнего, 3-го шага управления. Из условия задачи видно, что на 3-м шаге управление вынужденное, поэтому

Условную оптимизацию на 2-м шаге проводим с помощью рекуррентного уравнения

min

min

Пусть S₁=, тогда

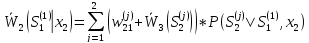
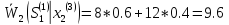
min

Далее оптимизируем 1–й шаг. и

Результат оптимизации

В кружках проставлены значения условных минимумов . Из рисунка видно, что оптимальное управление на 1-м шаге равно x₁⁽²⁾. Оно детерминировано переводит систему в S₁⁽¹⁾, где наилучшее управление заключается в применении x₁⁽³⁾. При этом система переходит в S₂⁽¹⁾ или в S₂⁽¹⁾, с вероятностями, равными 0,6 и 0,4 соответственно. Если переход осуществлен в S₂⁽¹⁾, то дальше надо применять x₃⁽¹⁾, если же в S₂⁽²⁾, то оптимальное шаговое управление здесь x₃⁽²⁾. В обоих случаях система переходит в S₃. Состояния S₁⁽²⁾ и S₁⁽³⁾ остаются незадействованными. Минимальное среднее время перехода из S₀ в S₃ составляет 11,6 единиц времени.

Пример 2:

В течение ближайших 3-х дней больному необходимо сделать срочную операцию. Для уменьшения риска неблагоприятного исхода желательно, чтобы состояние больного непосредственно перед операцией было наилучшим. С помощью медицинских обследований состояние больного оценивают по трехбалльной шкале, причем оценка 1 соответствует наихудшему состоянию S₁, 2 – промежуточному S₂, 3 – наилучшему S₃. Надо рассчитать оптимальную стратегию врача (т.е. в какой из трех дней лучше всего делать операцию), если вероятности наступления состояний S₁, S₂, S₃, и в любой день не зависят от состояния больного в предыдущий день и равны

p1=P(S1) =0,3; p2=P(S2) =0,5; p3=P(S3) =0,2;

Для решения этой задачи составим дерево альтернатив, изображенное на рис.2.13 Пусть z_i - оценка состояния больного, а x_i - принимаемое решение в i-й день. Тогда после измерения состояния больного в 1-й день (Изм1), если z₁=3, то x₁=[On], т.е. принимается решение оперировать; если z₁=1, то x1=[Жд]- ждать следующего дня, а если z₁=2, то возникает неопределенность (может быть принято, как одно, так и другое решение). Аналогичная ситуация возникает и на второй день после процедуры Изм2, если в 1-й день принято решение [Жд]. Таким образом задача заключается в выработке рекомендаций о принятии оптимальных решений, если в 1-й или во 2-й день состояние больного будет оценено как 2.

В качестве критерия оптимальности (целевой функции) будем использовать среднеожидаемую оценку состояния оперируемого больного, которую необходимо максимизировать. Пусть w_i^(j)- значение целевой функции на i-й день при z_i=j. Допустим, больного решили оперировать лишь на 3-й день. В этом случае среднеожидаемая оценка состояния больного перед операцией будет равна (рис. 2.14).

Этот результат показывает, что если на 2-й день мы получили z₂=2, то (так как это больше, чем 1,9) наилучшим будет решение x₂=<On> и для второго дня дерево альтернатив представляется в виде рис. 2.15. Из рисунка видно, что w₂⁽¹⁾ = w̅₃.Рассуждая аналогично, среднеожидаемая оценка состояния больного на 2-й день

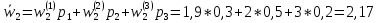
Это больше, чем 2, поэтому, если в 1-й день будет z₁=2,то оптимальным решением будет воздержаться от операции в надежде на улучшение состояния больного в оставшиеся два дня, и дерево альтернатив для первого дня приобретает вид рис. 2.16. Из этого рисунка видно, что w₁⁽¹⁾=w₁⁽²⁾=w̅₂. Наконец, среднеожидаемая оценка состояния больного в 1-й день

Это среднеожидаемая оценка состояния оперируемого больного, полученная за счет использования двух резервных дней. В случае, если бы эти дни не предоставлялись и больной бы оперировался всегда в 1-й день, среднеожидаемая оценка его состояния, как подсчитано выше, равнялась бы 1,9.

Таким образом, оптимальной стратегией врача будет следующая. Если в первый день состояние больного оценено на 3, то в этот день проводится операция. В случае же, если в первый день состояние больного оценивается меньше, чем на 3, решение об операции откладывается до следующего дня. Если на второй день состояние больного оценивается на 3 или на 2, то в этот день проводится операция. Если во второй день состояние больного оценено на 1, то операция откладывается на 3-й день. При такой тактике мы рассчитываем, что в момент операции состояние больного в среднем окажется равным 2,336 (вместо 1,9 при чисто случайной тактике).

В данном примере вместо хирургической операции могут, конечно, рассматриваться и другие существенные воздействия на организм человека, успешность применения которых критична к состоянию человека, меняющемуся во времени. Можно также переформулировать эту задачу как нахождение оптимального выбора момента выполнения ответственных действия человеком (спортивных достижений; специальных заданий, выполняемых в экстремальных условиях) в ограниченном интервале времени в условиях меняющегося во времени его физиологического или психологического состояния. При этом считается, что во всех промежуточных точках заданного интервала времени состояние человека может быть оценено количественно. Задачу можно существенно усложнить, если ввести зависимость данного состояния от предыдущего.