
- •Оглавление
- •Методы принятия оптимальных решений. Математические модели операции: детерминированный случай, оптимизация решений в условиях неопределенности.
- •Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
- •Оценка операции по нескольким показателям эффективности
- •Основная задача линейного программирования (озлп). Допустимые решения и оптимальное решение задачи лп.
- •Геометрическая интерпретация озлп.
- •Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
- •6. Симплекс-метод решения задачи лп
- •7. Табличный алгоритм замены переменных.
- •8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
- •9. Отыскание оптимального решения основной задачи линейного программирования на основе табличного алгоритма замены переменных.
- •10. Метод динамического программирования (дп). Алгоритм решения задач управления состоянием организма в биотехнических системах. Основное рекуррентное уравнение дп.
- •11. Управление переходом организма из исходного в конечное состояние методом дп: использование ориентированного графа.
- •12. Управление переходом организма из исходного в конечное состояние в условиях неопределенности.
- •13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
- •14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
- •15. Решение игры в смешанных стратегиях.
- •16. Игры 2х2 и их решение.
- •17. Геометрическая интерпретация решений игры 2х2.
- •18. Решение игр 2хn
- •19. Решение игр mx2
- •20. Решение игр mxn.
Оценка операции по нескольким показателям эффективности
S
– стоимость лекарств
W
– вероятность выздоровления пациента

W1, W2, Wk

Отбрасываем ненужные (большая стоимость или маленькая вероятность), далее решаем, что лучше.
-
Исп. составных критериев
 ;
;



-
 +
+ (взвешенная сумма)
(взвешенная сумма)
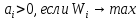


-
Сведение к одному показателю с некоторыми ограничениями, нахождение максимума первого показателя при ограничениях на оставшиеся

В рабочей области ab находится max значения
-
Основная задача линейного программирования (озлп). Допустимые решения и оптимальное решение задачи лп.
В разных практических задачах условия-ограничения имеют вид равенств, неравенств, а также и тех, и др.
Рассмотрим задачу с ограничениями-равенствами. Такая задача является ОЗЛП.
Дальше увидим, как от неравенств перейти к равенствам и наоборот.
Итак, формулировка основной задачи. Имеется ряд переменных x1, x2,…,xn.
Требуется найти такие неотрицательные значения этих переменных, которые бы удовлетворяли систему линейных уравнений следующего вида:
 ,
i=
,
i= ,
j=
,
j= (**)
(**)
И, кроме того, обращали бы линейную функцию L в min.
L= ,
xj-элементы
решений. (*)
,
xj-элементы
решений. (*)
В некоторых задачах функция L может максимизироваться, но ее также можн привести к стандартному виду, поменяв знак у ф-ции L.
Любая
совокупность решений xj ,
которая удовлетворяла условию (**),
называется допустимым
решением основной задачи (ДРОЗ)
,
которая удовлетворяла условию (**),
называется допустимым
решением основной задачи (ДРОЗ)
То или те из допустимых решений ОЗ, которые удовлетворяют условию (*), то ест обращают в min функцию L, составляют оптимальное решение.
Рассмотрим вопрос о существовании допустимых решений.
(**)



Не
имеет решений
Имеет
решения
В
обл. отриц. значений (
В
обл. неотриц. значений (ДРОЗ) )
)
ДРОЗ



Одно
решение
Решение
отсутствует
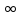 множество
множество
Открытая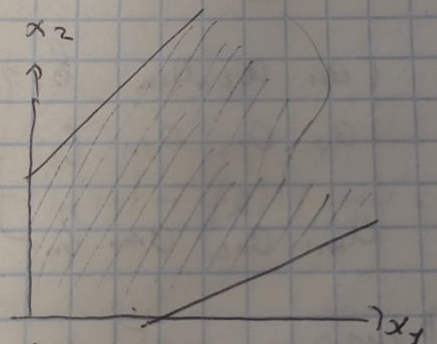



В
случае открытой обл. оптимальных
решений может не быть
Рассмотрим более подробно вопрос о существовании допустимых решений. В линейной алгебре доказывается, что для совместимости системы линейных уравнений необходимо и достаточно, чтобы ранг матрицы системы Zc был равен рангу расширенной матрицы системы Zp. В этом случае системы линейных уравнений имеют решения.
Матрицей
системы линейных уравнений называется
таблица, составленная из коэффициентов
при неизвестных
 ,
i=
,
i= ,
j=
,
j=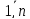
Расширенной
матрицей системы линейных уравнений
называется та же матрица, дополненная
столбцом свободных членов:
Рангом матрицы называется наибольший порядок отличного от нуля определителя, который можно получить, вычеркивая из матрицы какие-то строки и какие-то столбцы, чтобы перейти к квадратной матрице.
Пример 1. Определить, являются ли совместными следующие системы линейных уравнений.





 =
2*(-1)*(-2)+0+0-(-1)*(-1)*1-(-2)*1-0=5=>ri=3
=
2*(-1)*(-2)+0+0-(-1)*(-1)*1-(-2)*1-0=5=>ri=3
 =
5=
=
5= =>rp=ri=3.
r=3
система совместна
=>rp=ri=3.
r=3
система совместна
rp=ri=r
система совместна и полученное значение
является рангом линейных уравнений,
показывает число независимых линейных
уравнений r
 m,
r
m,
r
 n.
В дальнейшем будем рассматривать только
независимые уравнения=>r=m(1).r=n
в этом случае система имеет 1 решение.
n.
В дальнейшем будем рассматривать только
независимые уравнения=>r=m(1).r=n
в этом случае система имеет 1 решение.
Если
определитель матрицы
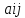 i=
i= ,
j=
,
j= ,
не равен 0, то находим решения для каждого
элемента решения j=
,
не равен 0, то находим решения для каждого
элемента решения j=
Для
области линейного программирования
этот вариант не уместен. Правда нужно
отметить: если xj .
.
Для
нас представляет интерес 2-й случай r=m,
r
<n
(2) в этом случае, решая систему, мы находим
целую область допустимых решений, т.е.
 множество значений для каждого неизвестно.
В зависимости от того n-m=2, то используется
геометрический способ решения. Если
(n-m)>2, то используется вычислительные
методы решения.
множество значений для каждого неизвестно.
В зависимости от того n-m=2, то используется
геометрический способ решения. Если
(n-m)>2, то используется вычислительные
методы решения.
(n-m) свободные
переменные. В области свободных переменных
будем искать ОДР, остальные переменные
назначаются базисными переменными. Они
дают ограничения в области допустимых
решений.
свободные
переменные. В области свободных переменных
будем искать ОДР, остальные переменные
назначаются базисными переменными. Они
дают ограничения в области допустимых
решений.
